立体几何中存在性问题的向量解法-重难点挑战-2022-2023学年高二数学人教A版(2019)选择性必修第一册(含解析)
文档属性
| 名称 | 立体几何中存在性问题的向量解法-重难点挑战-2022-2023学年高二数学人教A版(2019)选择性必修第一册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 17:06:10 | ||
图片预览


文档简介
立体几何中存在性问题的向量解法
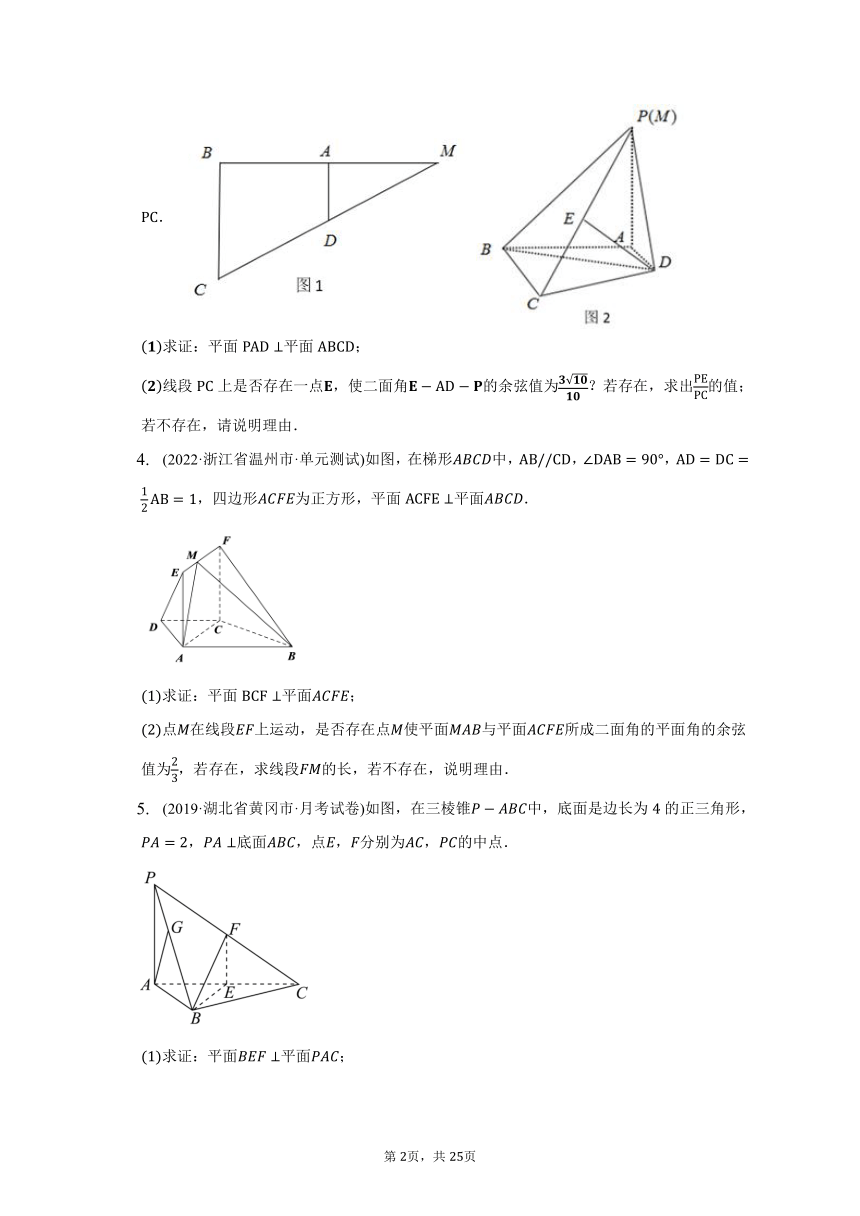
如图,在多面体中,平面平面,底面为直角梯形,,,,,.
证明:;
在线段上是否存在点,使得点到平面的距离为?若存在,求出的值;若不存在,说明理由.
(2022·吉林省长春市·期末考试)如图,三棱柱的所有棱长都是,平面,,分别是的中点.
求证:平面平面;
求平面和平面夹角的余弦值;
在线段含端点上是否存在点,使点到平面的距离为?请说明理由.
如图,在中,,,分别为棱,的中点,将沿折起到的位置,使,如图,连结,.
求证:平面平面;
线段上是否存在一点,使二面角的余弦值为?若存在,求出的值;若不存在,请说明理由.
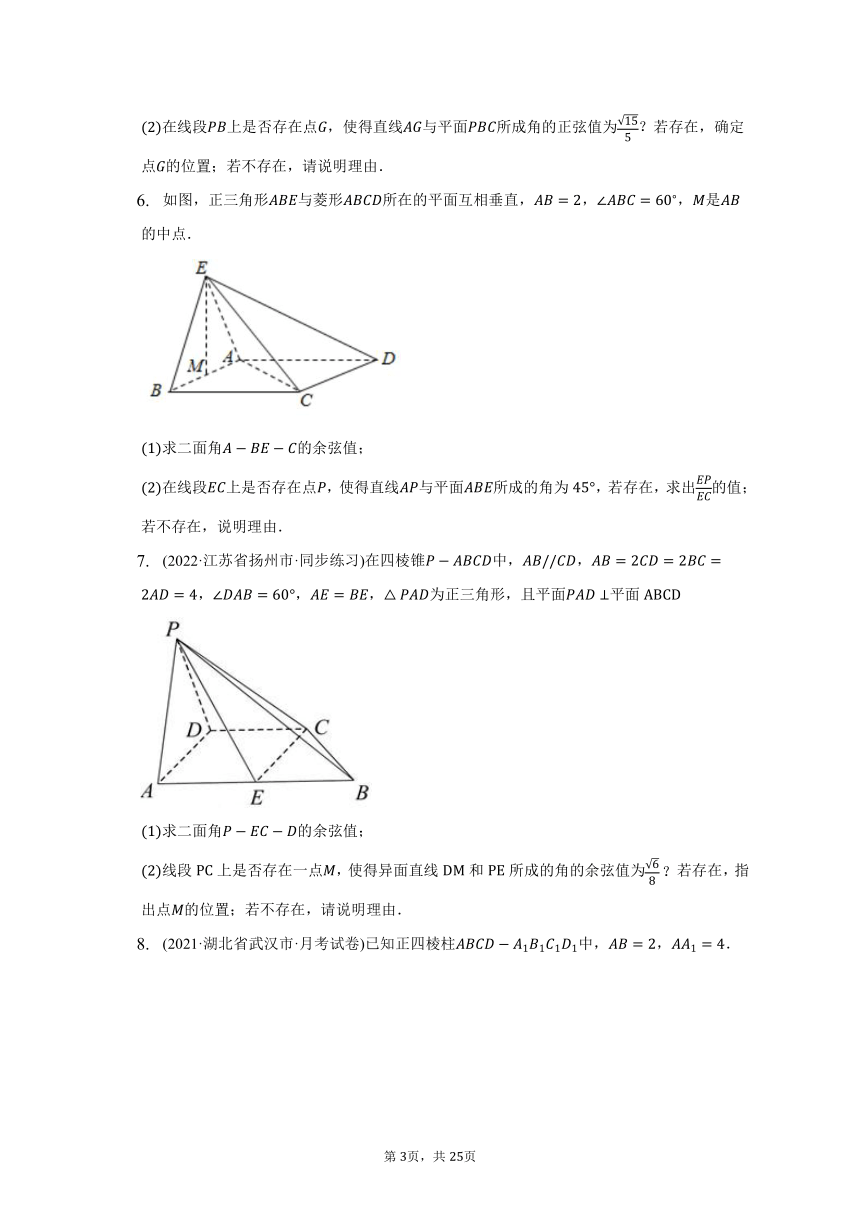
(2022·浙江省温州市·单元测试)如图,在梯形中,,,,四边形为正方形,平面平面.
求证:平面平面;
点在线段上运动,是否存在点使平面与平面所成二面角的平面角的余弦值为,若存在,求线段的长,若不存在,说明理由.
(2019·湖北省黄冈市·月考试卷)如图,在三棱锥中,底面是边长为的正三角形,,底面,点,分别为,的中点.
求证:平面平面;
在线段上是否存在点,使得直线与平面所成角的正弦值为?若存在,确定点的位置;若不存在,请说明理由.
如图,正三角形与菱形所在的平面互相垂直,,,是的中点.
求二面角的余弦值;
在线段上是否存在点,使得直线与平面所成的角为,若存在,求出的值;若不存在,说明理由.
(2022·江苏省扬州市·同步练习)在四棱锥中,,,,,为正三角形,且平面平面
求二面角的余弦值;
线段上是否存在一点,使得异面直线和所成的角的余弦值为若存在,指出点的位置;若不存在,请说明理由.
(2021·湖北省武汉市·月考试卷)已知正四棱柱中,,.
求证:;
求二面角的余弦值;
在线段上是否存在点,使得平面平面,若存在,求出的值;若不存在,请说明理由.
(2021·全国·期中考试)已知为等腰直角三角形,,,将沿底边上的高线折起到位置,使,如图所示,分别取,的中点,.
求二面角的余弦值
判断在线段上是否存在一点,使平面若存在,求出点的位置,若不存在,说明理由.
某市在滨海文化中心有滨海科技馆,其建筑有鲜明的后工业风格,如图所示,截取其中一部分抽象出长方体和圆台组合,如图所示,长方体中,,圆台下底圆心为的中点,直径为,圆与直线交于,圆台上底的圆心在上,直径为.
求与平面所成角的正弦值;
圆台上底圆周上是否存在一点使得,若存在,求点到直线的距离,若不存在则说明理由.
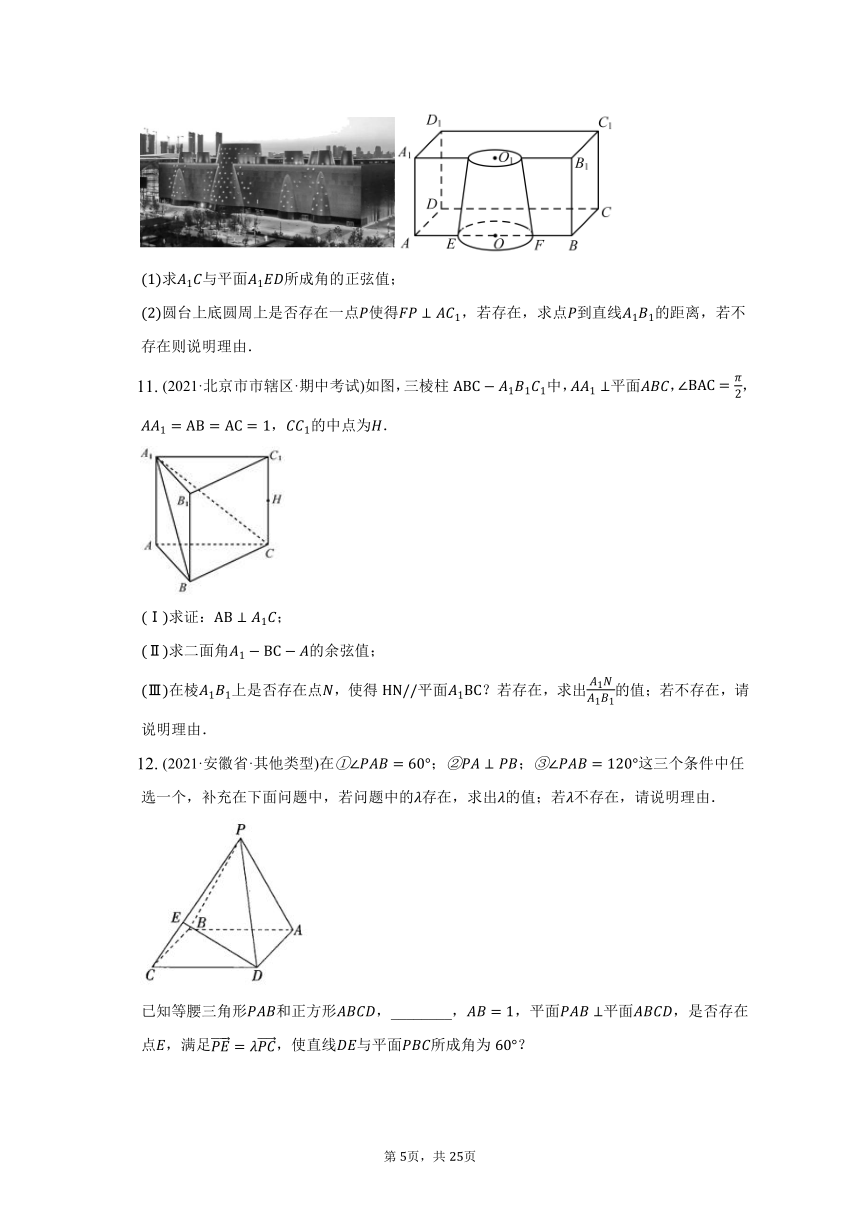
(2021·北京市市辖区·期中考试)如图,三棱柱中,平面,,,的中点为.
Ⅰ求证:;
Ⅱ求二面角的余弦值;
Ⅲ在棱上是否存在点,使得平面?若存在,求出的值;若不存在,请说明理由.
(2021·安徽省·其他类型)在;;这三个条件中任选一个,补充在下面问题中,若问题中的存在,求出的值;若不存在,请说明理由.
已知等腰三角形和正方形,________,,平面平面,是否存在点,满足,使直线与平面所成角为?
1.【答案】证明:因为,,,
所以,
所以,
因为平面平面,平面平面,平面,
所以平面,
因为平面,
所以.
解:存在满足题意的点,且.
由知平面且,
以为坐标原点,,,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图,
则,,,,,,
,,,
设,
则,
设平面的一个法向量为,
即
令,则.
设点到平面的距离为,
,
解得或舍.
所以在线段上存在点,且.
【解析】本题主要考查面面垂直,线面垂直及线线垂直的转化,利用空间向量计算空间距离.
根据题意得即,进而由面面垂直的性质可得线面垂直,最后可得线线垂直
结合的结论可建立空间直角坐标系,利用法向量及根据点到平面的距离为求解可得的值,进而可得的值.
2.【答案】解:取的中点,连接,则,,
又平面,所以平面,
所以两两垂直,
如图,以为原点,所在直线分别为轴,轴,
轴建立空间直角坐标系,
则,
证明:,
,
设分别为平面和平面的法向量,
由,
得
令,则,
是平面的一个法向量,
由,得
令,则,
是平面的一个法向量,
,
平面平面.
,设平面的法向量为.
由,得
令,则,,
是平面的一个法向量,
设平面和平面的夹角为,由图可知为锐角,
则,
即平面和平面夹角的余弦值为.
假设在线段含端点上存在点,
使点到平面的距离为,
设,则,
由,
解得:舍去或,
故在线段上存在点端点处,使点到平面的距离为.
【解析】本题考查利用空间向量法证明面面垂直,以及利用空间向量法求二面角余弦值和借助空间向量法求点到面的距离从而解决存在性问题,考查推理证明和运算能力,属于中档题.
取的中点,连接,易得两两垂直,建立空间直角坐标系,并求出各点坐标,
利用空间向量法,分别求出平面和平面的法向量:和,通过,即可证出平面平面;
先求出是平面的一个法向量,利用空间向量法求二面角公式,即可得出答案;
假设在线段含端点上存在点,使点到平面的距离为,设,通过向量法求点到面的距离公式,求出的值,即可得出结论.
3.【答案】证明:因为,分别为,中点,
所以,
因为,
所以,
所以,
因为,
所以,
又因为,,平面,
所以平面,
又因为平面,
所以平面平面;
解:因为,,,所以,,两两互相垂直,
以为坐标原点,建立如图所示的空间直角坐标系,
依题意由,,,,
假设线段上存在一点,使二面角的余弦值为,
设,,
则,
即,
所以,
,,
易得平面的一个法向量为,
设平面的一个法向量,
则有
令,则,
若二面角的余弦值为,
则有
,
由,解得.
故线段上存在一点,使二面角的余弦值为,且.
【解析】本题考查面面垂直的证明,利用空间向量法求二面角的余弦值解决探索性问题,属于拔高题.
推导出,,则可得,,从而平面,由此能证明平面平面;
以为坐标原点,建立空间直角坐标系,设,求出平面的一个法向量和平面的一个法向量,利用向量法求出即可.
4.【答案】证明:在梯形中,
因为,,,
所以,
又因为,取中点,连接,
则,,易知,
所以,
所以.
因为平面平面,平面平面,平面,
所以平面,
又平面.
所以平面平面;
由可建立分别以直线,,为轴,轴,轴的如图所示空间直角坐标系,
令,则,,,,
所以,,
设为平面的一个法向量,
由得
取,则,
因为是平面的一个法向量,
设平面与平面的夹角为,
所以,
可得,即.
【解析】本题给出特殊多面体,求证线面垂直并探索二面角的大小问题.着重考查了线面垂直、面面垂直的判定与性质和利用空间向量研究平面与平面所成角等知识点,属于较难题.
由题意证出,由平面平面,证出平面,结合面面垂直的判定定理即可证出平面平面;
建立分别以直线,,为轴,轴,轴的如图所示空间直角坐标系,令,求出面的一个法向量:,因为是平面的一个法向量,由可得.
5.【答案】证明:,为的中点,
,
又平面,平面,
,
,,平面,
平面,
平面,
平面平面;
解:存在,为线段的中点证明如下:
由知,,
点,分别为,中点,
,
,,
又,
,,两两垂直,
以为坐标原点,,,所在直线为轴,轴,轴,建立如图所示的空间直角坐标系,
则,,,,
设,
,
,
设平面的法向量,
则,
令,则,
得,
由已知,
即,
解得或舍去,
故,
故G为线段的中点.
【解析】本题考查线面垂直的判定与性质,面面垂直的判定,利用空间向量求线面所成的角,属于较难题.
证明,,进而可得平面,利用面面垂直的判定定理即可得证;
证明,,两两垂直,以为坐标原点,,,所在直线为轴,轴,轴,建立空间直角坐标系,利用空间向量法求出直线与平面所成角的正弦值,得出关系式求出点位置即可.
6.【答案】解:,是的中点,
,
平面平面,平面平面,平面,
平面,
平面,平面,
,
菱形中,,所以是正三角形,
.
、、两两垂直.
建立如图所示空间直角坐标系.
则,,,,
,,,
设是平面的一个法向量,
则,
令,得,
轴与平面垂直,
是平面的一个法向量.
,
又二面角的平面角为锐角,
二面角的余弦值为.
假设在线段上存在点,使得直线与平面所成的角为.
,,
设,,
则,
直线与平面所成的角为,
,
由,解得,
在线段上存在点,使得直线与平面所成的角为,且.
【解析】本题考查线线垂直的证明,考查二面角的余弦值的求法,考查满足条件的点是否存在的判断与求法,考查空间中线线、线面、面面间的位置关系等基础知识,是拔高题.
证明、、两两垂直,建立空间直角坐标系,利用向量法能求出二面角的余弦值.
求出和平面的法向量,利用向量法能求出在线段上存在点,使得直线与平面所成的角为,且.
7.【答案】解:设是中点,连接,,
因为为正三角形,
则,
又平面平面,平面平面,平面,
所以平面,
又,,
为正三角形,则,
以为原点,为轴,为轴,为轴,建立空间直角坐标系,如图,
则,,,,
设平面法向量为,
,,
则
取,得,
易得平面的法向量为,
,
可知二面角的平面角为锐角,
二面角的余弦值为
设,则,
,
,,
所以,
解得或,
所以当点为线段的三等分点时,异面直线和所成的角的余弦值为.
【解析】本题考查了平面与平面所成角的向量求法,直线与直线所成角的向量求法,属于较难题.
建立空间直角坐标系,得出平面法向量和平面的法向量,由空间向量求解即可;
设,利用空间向量求解异面直线和所成的角的余弦值,得出,可得结果.
8.【答案】解:因为四棱柱是正四棱柱,
所以平面,,
因为平面,
所以,
因为,
所以平面,
因为平面,
所以.
如图,以为原点建立空间直角坐标系,
则,,,,,,
,,,
因为平面,所以是平面的法向量,
设平面的法向量,
则
即
令,则,,
故,
因为二面角是钝二面角,
所以二面角的余弦值为.
设为线段上一点,,,
因为,,,
所以,
则,,,,,
设平面的法向量,
则
即
令,则,
若平面平面,
则,即,
解得,
故当时,平面平面.
【解析】本题考查异面直线垂直的证明,考查二面角的余弦值的求法,考查满足条件的点是否存在的判断,解题时要认真审题,注意向量法的合理运用.
本题首先可根据题意得出平面以及,然后根据线面垂直的性质得出,最后根据线面垂直的判定与性质即可证得结论;
首先可建立空间直角坐标系,然后求出平面的法向量,再然后求出平面的法向量,最后通过即可得出结果;
本题可设为线段上一点,,然后根据得出,再然后求出平面的法向量,最后通过即可得出结果.
9.【答案】解:由题知,,,且,
分别以,,所在三线为,,轴建立空间直角坐标系,
则点,,,,,
,,,设平面的法向量为,则得
得,当时,得
同理可得平面的一个法向量为
那么,所以二面角的余弦值为
假设在线段上存在一点,使平面,设,则由,得,
得
那么,当平面时,,
即存在实数,使,解得,
那么,即点是线段的中点时,平面.
【解析】本题考查由空间向量法求二面角,证明线面垂直,属于中档题.
由题以为坐标原点,分别以、、所在直线为,,轴建立空间直角坐标系,由点的坐标得向量坐标,求出平面的一个法向量,平面的一个法向量,由向量夹角得二面角;
假设在线段上存在一点,使平面,设,,由向量的线性运算得
,,当平面时,,即存在实数,使,求得得点是线段的中点.
10.【答案】解:由题意可知,建立空间直角坐标系如图所示,
则,,,,
所以,
设平面的法向量为,
则有,即,
令,,,故,
所以,
故A与平面所成角的正弦值为;
由可知,,,
所以,
假设存在这样的点,设,
由题意可知,
所以,因为,
则有,
所以,又,
所以,
解得舍,,
所以当时,,
此时点到直线的距离为.
【解析】本题考查了立体几何的综合应用,主要考查了线面角与点到线的距离的求解,属于中档题.
建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,求出直线的方向向量和平面的法向量,由线面角的计算公式求解即可;
假设存在点,利用点在底面圆上以及垂直关系,列出关于,的方程,求解即可.
11.【答案】解:Ⅰ因为平面,平面,所以,
又,所以,,平面
故AB平面,平面,
所以;
Ⅱ建立如图空间直角坐标系,
,,,,
设平面的一个法向量为,,
由,得,令,则,
又平面的法向量为,
由,
由题意知二面角为锐角,故二面角的余弦值为;
Ⅲ假设 上存在点,使得平面,
由,
由,,,
所以,
由平面,,得,满足题意;
故在棱上存在点,使得平面,的值为.
【解析】本题考查了线面垂直的性质,向量法在求二面角的余弦值中的应用,向量法确定点的存在性问题中的应用,属于中档题.
Ⅰ先证明平面,再证明即可;
Ⅱ建立空间直角坐标系,求出平面的一个法向量,又平面的法向量为,利用夹角公式求出即可;
Ⅲ假设 上存在点,使得平面,由,,得,再求出的坐标即可.
12.【答案】解:若选,则三角形为等边三角形,取的中点,
连接,则,又平面平面,
平面平面,所以平面,
以为原点,直线为轴,直线为轴,
建立如下图所示的空间直角坐标系,
则,
,
,
设是平面的一个法向量,
则
令,得,
是平面的一个法向量,
由直线与平面所成角为,
得,
即,
,
解得或,
存在点与重合,即时满足条件,
或点为中点,即时满足条件.
若选,则三角形为等腰直角三角形,
取的中点,连接,则,
又平面平面,平面平面,
所以平面,
以为原点,直线为轴,直线为轴,
建立如下图所示的空间直角坐标系,
则,
,
,
设是平面的一个法向量,
则
令,得,
是平面的一个法向量,
由直线与平面所成角为,
得,
即,
,
,方程无解,
即不存在,满足,使直线与平面所成角为.
若选,则,过点作,垂足为,
又平面平面,平面平面,
所以平面,
以为原点,直线为轴,直线为轴,
建立如下图所示的空间直角坐标系,
则,
,
,
设是平面的一个法向量,
则
令,得,
是平面的一个法向量,
由直线与平面所成角为,
得,
即,
,方程无解,
即不存在,满足,使直线与平面所成角为.
【解析】本题主要考查利用空间向量法求线面角问题,还考查了空间想象和运算求解的能力,属于中档题.
若选,则三角形为等边三角形,取的中点,连接,再根据平面平面,利用面面垂直的性质定理得到平面,然后以为原点,直线为轴,直线为轴,建立的空间直角坐标系,求得平面的一个法向量和由表示向量的坐标,由求解.
选,同理,建立坐标系,求出平面法向量以及向量,由求解即可
第1页,共1页
如图,在多面体中,平面平面,底面为直角梯形,,,,,.
证明:;
在线段上是否存在点,使得点到平面的距离为?若存在,求出的值;若不存在,说明理由.
(2022·吉林省长春市·期末考试)如图,三棱柱的所有棱长都是,平面,,分别是的中点.
求证:平面平面;
求平面和平面夹角的余弦值;
在线段含端点上是否存在点,使点到平面的距离为?请说明理由.
如图,在中,,,分别为棱,的中点,将沿折起到的位置,使,如图,连结,.
求证:平面平面;
线段上是否存在一点,使二面角的余弦值为?若存在,求出的值;若不存在,请说明理由.
(2022·浙江省温州市·单元测试)如图,在梯形中,,,,四边形为正方形,平面平面.
求证:平面平面;
点在线段上运动,是否存在点使平面与平面所成二面角的平面角的余弦值为,若存在,求线段的长,若不存在,说明理由.
(2019·湖北省黄冈市·月考试卷)如图,在三棱锥中,底面是边长为的正三角形,,底面,点,分别为,的中点.
求证:平面平面;
在线段上是否存在点,使得直线与平面所成角的正弦值为?若存在,确定点的位置;若不存在,请说明理由.
如图,正三角形与菱形所在的平面互相垂直,,,是的中点.
求二面角的余弦值;
在线段上是否存在点,使得直线与平面所成的角为,若存在,求出的值;若不存在,说明理由.
(2022·江苏省扬州市·同步练习)在四棱锥中,,,,,为正三角形,且平面平面
求二面角的余弦值;
线段上是否存在一点,使得异面直线和所成的角的余弦值为若存在,指出点的位置;若不存在,请说明理由.
(2021·湖北省武汉市·月考试卷)已知正四棱柱中,,.
求证:;
求二面角的余弦值;
在线段上是否存在点,使得平面平面,若存在,求出的值;若不存在,请说明理由.
(2021·全国·期中考试)已知为等腰直角三角形,,,将沿底边上的高线折起到位置,使,如图所示,分别取,的中点,.
求二面角的余弦值
判断在线段上是否存在一点,使平面若存在,求出点的位置,若不存在,说明理由.
某市在滨海文化中心有滨海科技馆,其建筑有鲜明的后工业风格,如图所示,截取其中一部分抽象出长方体和圆台组合,如图所示,长方体中,,圆台下底圆心为的中点,直径为,圆与直线交于,圆台上底的圆心在上,直径为.
求与平面所成角的正弦值;
圆台上底圆周上是否存在一点使得,若存在,求点到直线的距离,若不存在则说明理由.
(2021·北京市市辖区·期中考试)如图,三棱柱中,平面,,,的中点为.
Ⅰ求证:;
Ⅱ求二面角的余弦值;
Ⅲ在棱上是否存在点,使得平面?若存在,求出的值;若不存在,请说明理由.
(2021·安徽省·其他类型)在;;这三个条件中任选一个,补充在下面问题中,若问题中的存在,求出的值;若不存在,请说明理由.
已知等腰三角形和正方形,________,,平面平面,是否存在点,满足,使直线与平面所成角为?
1.【答案】证明:因为,,,
所以,
所以,
因为平面平面,平面平面,平面,
所以平面,
因为平面,
所以.
解:存在满足题意的点,且.
由知平面且,
以为坐标原点,,,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图,
则,,,,,,
,,,
设,
则,
设平面的一个法向量为,
即
令,则.
设点到平面的距离为,
,
解得或舍.
所以在线段上存在点,且.
【解析】本题主要考查面面垂直,线面垂直及线线垂直的转化,利用空间向量计算空间距离.
根据题意得即,进而由面面垂直的性质可得线面垂直,最后可得线线垂直
结合的结论可建立空间直角坐标系,利用法向量及根据点到平面的距离为求解可得的值,进而可得的值.
2.【答案】解:取的中点,连接,则,,
又平面,所以平面,
所以两两垂直,
如图,以为原点,所在直线分别为轴,轴,
轴建立空间直角坐标系,
则,
证明:,
,
设分别为平面和平面的法向量,
由,
得
令,则,
是平面的一个法向量,
由,得
令,则,
是平面的一个法向量,
,
平面平面.
,设平面的法向量为.
由,得
令,则,,
是平面的一个法向量,
设平面和平面的夹角为,由图可知为锐角,
则,
即平面和平面夹角的余弦值为.
假设在线段含端点上存在点,
使点到平面的距离为,
设,则,
由,
解得:舍去或,
故在线段上存在点端点处,使点到平面的距离为.
【解析】本题考查利用空间向量法证明面面垂直,以及利用空间向量法求二面角余弦值和借助空间向量法求点到面的距离从而解决存在性问题,考查推理证明和运算能力,属于中档题.
取的中点,连接,易得两两垂直,建立空间直角坐标系,并求出各点坐标,
利用空间向量法,分别求出平面和平面的法向量:和,通过,即可证出平面平面;
先求出是平面的一个法向量,利用空间向量法求二面角公式,即可得出答案;
假设在线段含端点上存在点,使点到平面的距离为,设,通过向量法求点到面的距离公式,求出的值,即可得出结论.
3.【答案】证明:因为,分别为,中点,
所以,
因为,
所以,
所以,
因为,
所以,
又因为,,平面,
所以平面,
又因为平面,
所以平面平面;
解:因为,,,所以,,两两互相垂直,
以为坐标原点,建立如图所示的空间直角坐标系,
依题意由,,,,
假设线段上存在一点,使二面角的余弦值为,
设,,
则,
即,
所以,
,,
易得平面的一个法向量为,
设平面的一个法向量,
则有
令,则,
若二面角的余弦值为,
则有
,
由,解得.
故线段上存在一点,使二面角的余弦值为,且.
【解析】本题考查面面垂直的证明,利用空间向量法求二面角的余弦值解决探索性问题,属于拔高题.
推导出,,则可得,,从而平面,由此能证明平面平面;
以为坐标原点,建立空间直角坐标系,设,求出平面的一个法向量和平面的一个法向量,利用向量法求出即可.
4.【答案】证明:在梯形中,
因为,,,
所以,
又因为,取中点,连接,
则,,易知,
所以,
所以.
因为平面平面,平面平面,平面,
所以平面,
又平面.
所以平面平面;
由可建立分别以直线,,为轴,轴,轴的如图所示空间直角坐标系,
令,则,,,,
所以,,
设为平面的一个法向量,
由得
取,则,
因为是平面的一个法向量,
设平面与平面的夹角为,
所以,
可得,即.
【解析】本题给出特殊多面体,求证线面垂直并探索二面角的大小问题.着重考查了线面垂直、面面垂直的判定与性质和利用空间向量研究平面与平面所成角等知识点,属于较难题.
由题意证出,由平面平面,证出平面,结合面面垂直的判定定理即可证出平面平面;
建立分别以直线,,为轴,轴,轴的如图所示空间直角坐标系,令,求出面的一个法向量:,因为是平面的一个法向量,由可得.
5.【答案】证明:,为的中点,
,
又平面,平面,
,
,,平面,
平面,
平面,
平面平面;
解:存在,为线段的中点证明如下:
由知,,
点,分别为,中点,
,
,,
又,
,,两两垂直,
以为坐标原点,,,所在直线为轴,轴,轴,建立如图所示的空间直角坐标系,
则,,,,
设,
,
,
设平面的法向量,
则,
令,则,
得,
由已知,
即,
解得或舍去,
故,
故G为线段的中点.
【解析】本题考查线面垂直的判定与性质,面面垂直的判定,利用空间向量求线面所成的角,属于较难题.
证明,,进而可得平面,利用面面垂直的判定定理即可得证;
证明,,两两垂直,以为坐标原点,,,所在直线为轴,轴,轴,建立空间直角坐标系,利用空间向量法求出直线与平面所成角的正弦值,得出关系式求出点位置即可.
6.【答案】解:,是的中点,
,
平面平面,平面平面,平面,
平面,
平面,平面,
,
菱形中,,所以是正三角形,
.
、、两两垂直.
建立如图所示空间直角坐标系.
则,,,,
,,,
设是平面的一个法向量,
则,
令,得,
轴与平面垂直,
是平面的一个法向量.
,
又二面角的平面角为锐角,
二面角的余弦值为.
假设在线段上存在点,使得直线与平面所成的角为.
,,
设,,
则,
直线与平面所成的角为,
,
由,解得,
在线段上存在点,使得直线与平面所成的角为,且.
【解析】本题考查线线垂直的证明,考查二面角的余弦值的求法,考查满足条件的点是否存在的判断与求法,考查空间中线线、线面、面面间的位置关系等基础知识,是拔高题.
证明、、两两垂直,建立空间直角坐标系,利用向量法能求出二面角的余弦值.
求出和平面的法向量,利用向量法能求出在线段上存在点,使得直线与平面所成的角为,且.
7.【答案】解:设是中点,连接,,
因为为正三角形,
则,
又平面平面,平面平面,平面,
所以平面,
又,,
为正三角形,则,
以为原点,为轴,为轴,为轴,建立空间直角坐标系,如图,
则,,,,
设平面法向量为,
,,
则
取,得,
易得平面的法向量为,
,
可知二面角的平面角为锐角,
二面角的余弦值为
设,则,
,
,,
所以,
解得或,
所以当点为线段的三等分点时,异面直线和所成的角的余弦值为.
【解析】本题考查了平面与平面所成角的向量求法,直线与直线所成角的向量求法,属于较难题.
建立空间直角坐标系,得出平面法向量和平面的法向量,由空间向量求解即可;
设,利用空间向量求解异面直线和所成的角的余弦值,得出,可得结果.
8.【答案】解:因为四棱柱是正四棱柱,
所以平面,,
因为平面,
所以,
因为,
所以平面,
因为平面,
所以.
如图,以为原点建立空间直角坐标系,
则,,,,,,
,,,
因为平面,所以是平面的法向量,
设平面的法向量,
则
即
令,则,,
故,
因为二面角是钝二面角,
所以二面角的余弦值为.
设为线段上一点,,,
因为,,,
所以,
则,,,,,
设平面的法向量,
则
即
令,则,
若平面平面,
则,即,
解得,
故当时,平面平面.
【解析】本题考查异面直线垂直的证明,考查二面角的余弦值的求法,考查满足条件的点是否存在的判断,解题时要认真审题,注意向量法的合理运用.
本题首先可根据题意得出平面以及,然后根据线面垂直的性质得出,最后根据线面垂直的判定与性质即可证得结论;
首先可建立空间直角坐标系,然后求出平面的法向量,再然后求出平面的法向量,最后通过即可得出结果;
本题可设为线段上一点,,然后根据得出,再然后求出平面的法向量,最后通过即可得出结果.
9.【答案】解:由题知,,,且,
分别以,,所在三线为,,轴建立空间直角坐标系,
则点,,,,,
,,,设平面的法向量为,则得
得,当时,得
同理可得平面的一个法向量为
那么,所以二面角的余弦值为
假设在线段上存在一点,使平面,设,则由,得,
得
那么,当平面时,,
即存在实数,使,解得,
那么,即点是线段的中点时,平面.
【解析】本题考查由空间向量法求二面角,证明线面垂直,属于中档题.
由题以为坐标原点,分别以、、所在直线为,,轴建立空间直角坐标系,由点的坐标得向量坐标,求出平面的一个法向量,平面的一个法向量,由向量夹角得二面角;
假设在线段上存在一点,使平面,设,,由向量的线性运算得
,,当平面时,,即存在实数,使,求得得点是线段的中点.
10.【答案】解:由题意可知,建立空间直角坐标系如图所示,
则,,,,
所以,
设平面的法向量为,
则有,即,
令,,,故,
所以,
故A与平面所成角的正弦值为;
由可知,,,
所以,
假设存在这样的点,设,
由题意可知,
所以,因为,
则有,
所以,又,
所以,
解得舍,,
所以当时,,
此时点到直线的距离为.
【解析】本题考查了立体几何的综合应用,主要考查了线面角与点到线的距离的求解,属于中档题.
建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,求出直线的方向向量和平面的法向量,由线面角的计算公式求解即可;
假设存在点,利用点在底面圆上以及垂直关系,列出关于,的方程,求解即可.
11.【答案】解:Ⅰ因为平面,平面,所以,
又,所以,,平面
故AB平面,平面,
所以;
Ⅱ建立如图空间直角坐标系,
,,,,
设平面的一个法向量为,,
由,得,令,则,
又平面的法向量为,
由,
由题意知二面角为锐角,故二面角的余弦值为;
Ⅲ假设 上存在点,使得平面,
由,
由,,,
所以,
由平面,,得,满足题意;
故在棱上存在点,使得平面,的值为.
【解析】本题考查了线面垂直的性质,向量法在求二面角的余弦值中的应用,向量法确定点的存在性问题中的应用,属于中档题.
Ⅰ先证明平面,再证明即可;
Ⅱ建立空间直角坐标系,求出平面的一个法向量,又平面的法向量为,利用夹角公式求出即可;
Ⅲ假设 上存在点,使得平面,由,,得,再求出的坐标即可.
12.【答案】解:若选,则三角形为等边三角形,取的中点,
连接,则,又平面平面,
平面平面,所以平面,
以为原点,直线为轴,直线为轴,
建立如下图所示的空间直角坐标系,
则,
,
,
设是平面的一个法向量,
则
令,得,
是平面的一个法向量,
由直线与平面所成角为,
得,
即,
,
解得或,
存在点与重合,即时满足条件,
或点为中点,即时满足条件.
若选,则三角形为等腰直角三角形,
取的中点,连接,则,
又平面平面,平面平面,
所以平面,
以为原点,直线为轴,直线为轴,
建立如下图所示的空间直角坐标系,
则,
,
,
设是平面的一个法向量,
则
令,得,
是平面的一个法向量,
由直线与平面所成角为,
得,
即,
,
,方程无解,
即不存在,满足,使直线与平面所成角为.
若选,则,过点作,垂足为,
又平面平面,平面平面,
所以平面,
以为原点,直线为轴,直线为轴,
建立如下图所示的空间直角坐标系,
则,
,
,
设是平面的一个法向量,
则
令,得,
是平面的一个法向量,
由直线与平面所成角为,
得,
即,
,方程无解,
即不存在,满足,使直线与平面所成角为.
【解析】本题主要考查利用空间向量法求线面角问题,还考查了空间想象和运算求解的能力,属于中档题.
若选,则三角形为等边三角形,取的中点,连接,再根据平面平面,利用面面垂直的性质定理得到平面,然后以为原点,直线为轴,直线为轴,建立的空间直角坐标系,求得平面的一个法向量和由表示向量的坐标,由求解.
选,同理,建立坐标系,求出平面法向量以及向量,由求解即可
第1页,共1页
