立体几何中的轨迹问题-重难点挑战-2022-2023学年高二数学人教A版(2019)选择性必修第一册(含解析)
文档属性
| 名称 | 立体几何中的轨迹问题-重难点挑战-2022-2023学年高二数学人教A版(2019)选择性必修第一册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 724.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 17:07:04 | ||
图片预览



文档简介
立体几何中的轨迹问题
(2021·浙江省金华市·单元测试)在棱长为的正方体中,点为中点,点在侧面及其边界上移动,并且总是保持,则动点的轨迹的长度为( )
A. B. C. D.
(2020·山东省·同步练习)底面为正方形的四棱锥,且平面,,,线段上一点满足,为线段的中点,为四棱锥表面上一点,且,则点形成的轨迹的长度为( )
A. B. C. D.
已知正方体的棱长为,、分别是棱、的中点,点为底面内包括边界的一动点,若直线与平面无公共点,则点的轨迹长度为( )
A. B. C. D.
(2021·安徽省滁州市·期末考试)在棱长为的正方体中,,分别是,的中点.点在该正方体的表面上运动,则总能使与垂直的点所构成的轨迹的周长等于( )
A.
B.
C.
D.
(2020·安徽省六安市·单元测试)在棱长为的正方体中,点在侧面上运动.若点到点的距离为,则动点的轨迹在正方形内的一段曲线长为( )
A.
B.
C.
D.
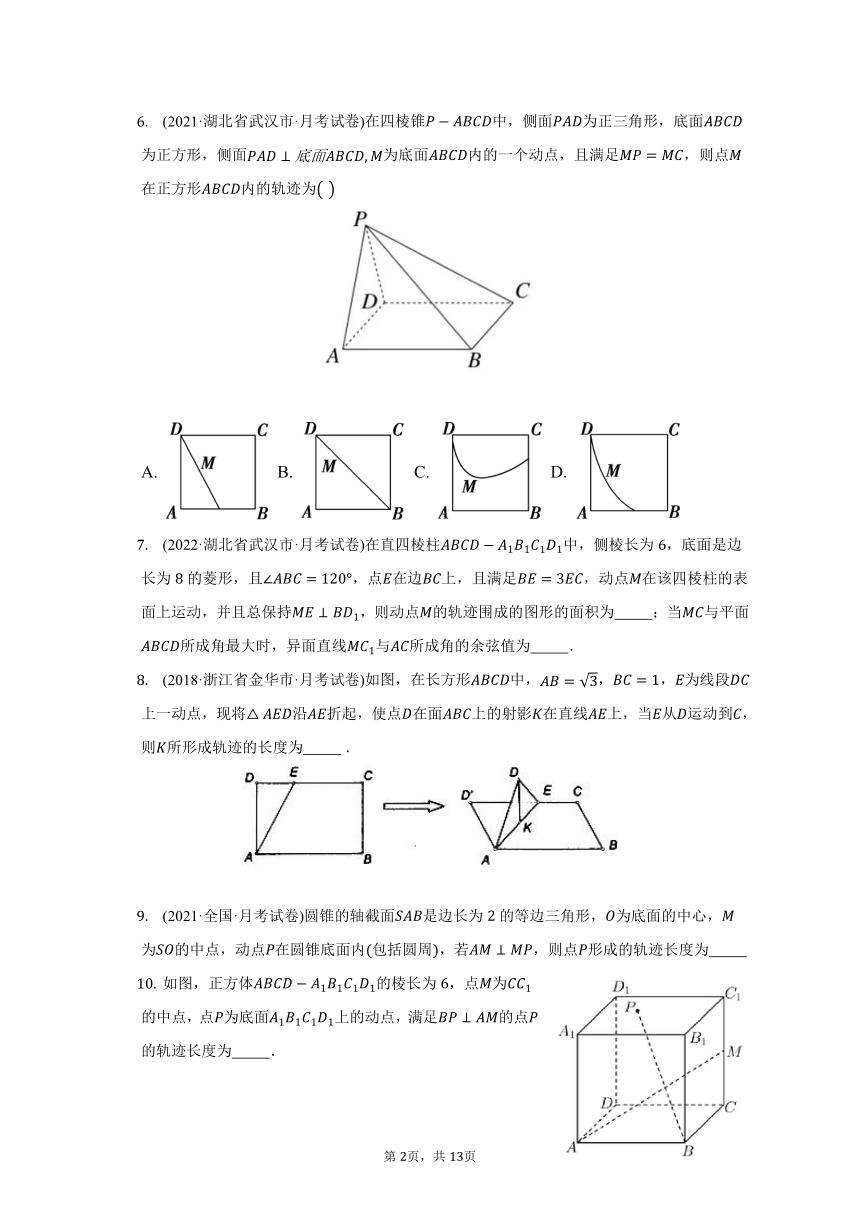
(2021·湖北省武汉市·月考试卷)在四棱锥中,侧面为正三角形,底面为正方形,侧面为底面内的一个动点,且满足,则点在正方形内的轨迹为
A. B. C. D.
(2022·湖北省武汉市·月考试卷)在直四棱柱中,侧棱长为,底面是边长为的菱形,且,点在边上,且满足,动点在该四棱柱的表面上运动,并且总保持,则动点的轨迹围成的图形的面积为 ;当与平面所成角最大时,异面直线与所成角的余弦值为 .
(2018·浙江省金华市·月考试卷)如图,在长方形中,,,为线段上一动点,现将沿折起,使点在面上的射影在直线上,当从运动到,则所形成轨迹的长度为 .
(2021·全国·月考试卷)圆锥的轴截面是边长为的等边三角形,为底面的中心,为的中点,动点在圆锥底面内包括圆周,若,则点形成的轨迹长度为
如图,正方体的棱长为,点为的中点,点为底面上的动点,满足的点的轨迹长度为 .
1.【答案】
【解析】
【分析】
本题考查了正方体中点的轨迹问题,属于中等题.
通过找到过且垂直于的平面,由题可知此平面与侧面的交线即为点的轨迹.
【解答】
解:设中点为,中点为,连接于,连接交于,
因为,,
又,、,
所以,
又,
所以,
而,所以有,因为,所以,
又,所以,
又,所以,
因为,所以,即,
和是平面内两条相交直线,所以,
又,所以在平面上,
故平面即为过且垂直于的平面,
它和侧面的交线即为点的轨迹,即为.
故动点的轨迹的长度为.
2.【答案】
【解析】
【分析】
本题考查通过建立空间直角坐标系,利用空间向量判定线线垂直,理解轨迹的概念,属于中档题.
取的中点,则,利用向量求出上一点,使得,故而点轨迹为除去点,由此求三角形周长即可.
【解答】
解:以为坐标原点,以,,为坐标轴建立空间直角坐标系,如图所示:
则,,,,,
取的中点,则,
,,
,即,
在上取一点,设,则,
设,则,
即,计算得出,
又
平面,
点轨迹为除去点,
,,
的周长为,
故选D.
3.【答案】
【解析】
【分析】
本题考查了正方体的结构特征应用问题,也考查了利用向量法判定直线与平面平行,是中档题.
设点,利用向量法求出与的值,进而可得轨迹长度。
【解答】
解:根据题意,以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,
则、、、,设点,
,,设平面的法向量为,由,取,可得,
,由题意可知,平面,则,
令,可得;令,可得.
易知点的轨迹交线段于点,交线段的中点,
因此点的轨迹长度为.
4.【答案】
【解析】
【分析】
本题主要考查了立体几何中的轨迹问题,线面垂直的判定,考查学生的分析解决问题的能力,属于中档题.
取的中点,设交于点,根据线面垂直的判定可得使与垂直的点所构成的轨迹为矩形,即可得解.
【解答】
解:如图,取的中点,连接,,,设交于点,则,
平面,平面,
,
正方体的棱长为,,分别是,的中点,
,,
,
,
,即,
又,、平面,
平面,
使与垂直的点所构成的轨迹为矩形,
正方体的棱长为,
由勾股定理可得,使与垂直的点所构成的轨迹的周长等于.
故选:.
5.【答案】
【解析】
【分析】
本题以正方体为载体,考查轨迹,考查曲线的周长,属于较难题.
本题首先要弄清楚曲线的形状,再根据曲线的性质及解析几何知识即可求出长度.
【解答】
解:由题意得动点的轨迹是以为球心,
半径为的球面被平面截得的小圆上,结合正方体,所以侧面,所以为截面圆的圆心,故 B皆为截面圆的半径,易知
截面半径为,
由所以点轨迹即弧长.
故选D.
6.【答案】
【解析】
【分析】
本题考查了空间动点的轨迹,四棱锥的结构特征和面面垂直的性质,同时考查了空间想象能力,推理能力,属于中档题.
先找符合条件的特殊位置,然后根据符合条件的轨迹为线段的垂直平分面与平面的交线得到的轨迹.
【解答】
解:根据题意可知,
则点符合“为底面内的一个动点,且满足”,
设的中点为,
因为侧面底面,侧面底面,
,底面,
所以侧面,又侧面,
所以,
根据题目条件可知≌,
,点也符合“为底面内的一个动点,且满足”,
故动点的轨迹肯定过点和点,
而到点与到点的距离相等的点为线段的垂直平分面,
线段的垂直平分面与平面的交线是一直线
故选A.
7.【答案】
【解析】
【分析】
本题考查利用空间向量法解决立体几何问题,考查直观想象与数学运算的核心素养,属于拔高题.
首先可证,在上取,使得,连接,则,可得记与的交点为,以为坐标原点,建立空间直角坐标系,在上取一点,由,求出点的位置,从而得到动点轨迹,即可求出动点的轨迹围成的图形的面积,显然当与重合时,与平面所成角最大,利用空间向量法求异面直线所成角的余弦值.
【解答】
解:如图,
在直四棱柱中,因为底面是菱形,侧棱垂直底面,
所以平面,
又平面,
所以.
在上取,使得,连接,则,所以.
记与的交点为,以为坐标原点,建立如图所示的空间直角坐标系,
则,,.
在上取一点,记为,于是,.
由,得,即,
所以的边为点的运动轨迹.
由题意得,,
动点的轨迹围成的图形的面积为.
显然当与重合时,与平面所成角最大.
因为,,
所以,,
因为直线的一个方向向量为,
所以,
即异面直线与所成角的余弦值为.
故答案为:;.
8.【答案】
【解析】
【分析】
本题考查线面垂直的性质和与弧长有关的轨迹问题,属于中档题.
由题意可得平面,故DK,则,故K点在以为直径的圆上,连接交此圆于点,则圆弧就是点的轨迹,利用弧长公式求出轨迹长度.
【解答】
解:由题意,点在面上的射影在直线上,易得平面,平面,故DK,
则,故K点在以为直径的圆上,如图,连接交此圆于点,
则圆弧就是点的轨迹,设圆心为,
在长方形中,,,则易得,则,
其所对的弧长为,
故答案为:.
9.【答案】
【解析】
【分析】
本题考查空间中直线与直线的位置关系,属于中档题.
由判断出所在的平面,从而推断出点形成的轨迹长度,再用几何的知识求出即可.
【解答】
解:过点作点垂线交于点,交底面圆于点,
连接,,,
底面圆,又,,
又面,
面,面,
,又,面,
面,又面,
,,
在中得,
可得点形成的轨迹长度为.
故答案为.
10.【答案】
【解析】
【分析】
本题考查正方体的结构特征,立体几何轨迹问题,考查线线垂直的向量表示,属于中档题.
根据题意以为原点建立空间直角坐标系,由,可得,分析得点的轨迹为的长度,计算可得.
【解答】
解:如图以为原点建立空间直角坐标系,
,,,
设,其中,,
,,
,
,即,
,
即,
又,,
点的轨迹为面上的直线,所示部分,即图中的长度,
由图知,
故答案为:.
第1页,共1页
(2021·浙江省金华市·单元测试)在棱长为的正方体中,点为中点,点在侧面及其边界上移动,并且总是保持,则动点的轨迹的长度为( )
A. B. C. D.
(2020·山东省·同步练习)底面为正方形的四棱锥,且平面,,,线段上一点满足,为线段的中点,为四棱锥表面上一点,且,则点形成的轨迹的长度为( )
A. B. C. D.
已知正方体的棱长为,、分别是棱、的中点,点为底面内包括边界的一动点,若直线与平面无公共点,则点的轨迹长度为( )
A. B. C. D.
(2021·安徽省滁州市·期末考试)在棱长为的正方体中,,分别是,的中点.点在该正方体的表面上运动,则总能使与垂直的点所构成的轨迹的周长等于( )
A.
B.
C.
D.
(2020·安徽省六安市·单元测试)在棱长为的正方体中,点在侧面上运动.若点到点的距离为,则动点的轨迹在正方形内的一段曲线长为( )
A.
B.
C.
D.
(2021·湖北省武汉市·月考试卷)在四棱锥中,侧面为正三角形,底面为正方形,侧面为底面内的一个动点,且满足,则点在正方形内的轨迹为
A. B. C. D.
(2022·湖北省武汉市·月考试卷)在直四棱柱中,侧棱长为,底面是边长为的菱形,且,点在边上,且满足,动点在该四棱柱的表面上运动,并且总保持,则动点的轨迹围成的图形的面积为 ;当与平面所成角最大时,异面直线与所成角的余弦值为 .
(2018·浙江省金华市·月考试卷)如图,在长方形中,,,为线段上一动点,现将沿折起,使点在面上的射影在直线上,当从运动到,则所形成轨迹的长度为 .
(2021·全国·月考试卷)圆锥的轴截面是边长为的等边三角形,为底面的中心,为的中点,动点在圆锥底面内包括圆周,若,则点形成的轨迹长度为
如图,正方体的棱长为,点为的中点,点为底面上的动点,满足的点的轨迹长度为 .
1.【答案】
【解析】
【分析】
本题考查了正方体中点的轨迹问题,属于中等题.
通过找到过且垂直于的平面,由题可知此平面与侧面的交线即为点的轨迹.
【解答】
解:设中点为,中点为,连接于,连接交于,
因为,,
又,、,
所以,
又,
所以,
而,所以有,因为,所以,
又,所以,
又,所以,
因为,所以,即,
和是平面内两条相交直线,所以,
又,所以在平面上,
故平面即为过且垂直于的平面,
它和侧面的交线即为点的轨迹,即为.
故动点的轨迹的长度为.
2.【答案】
【解析】
【分析】
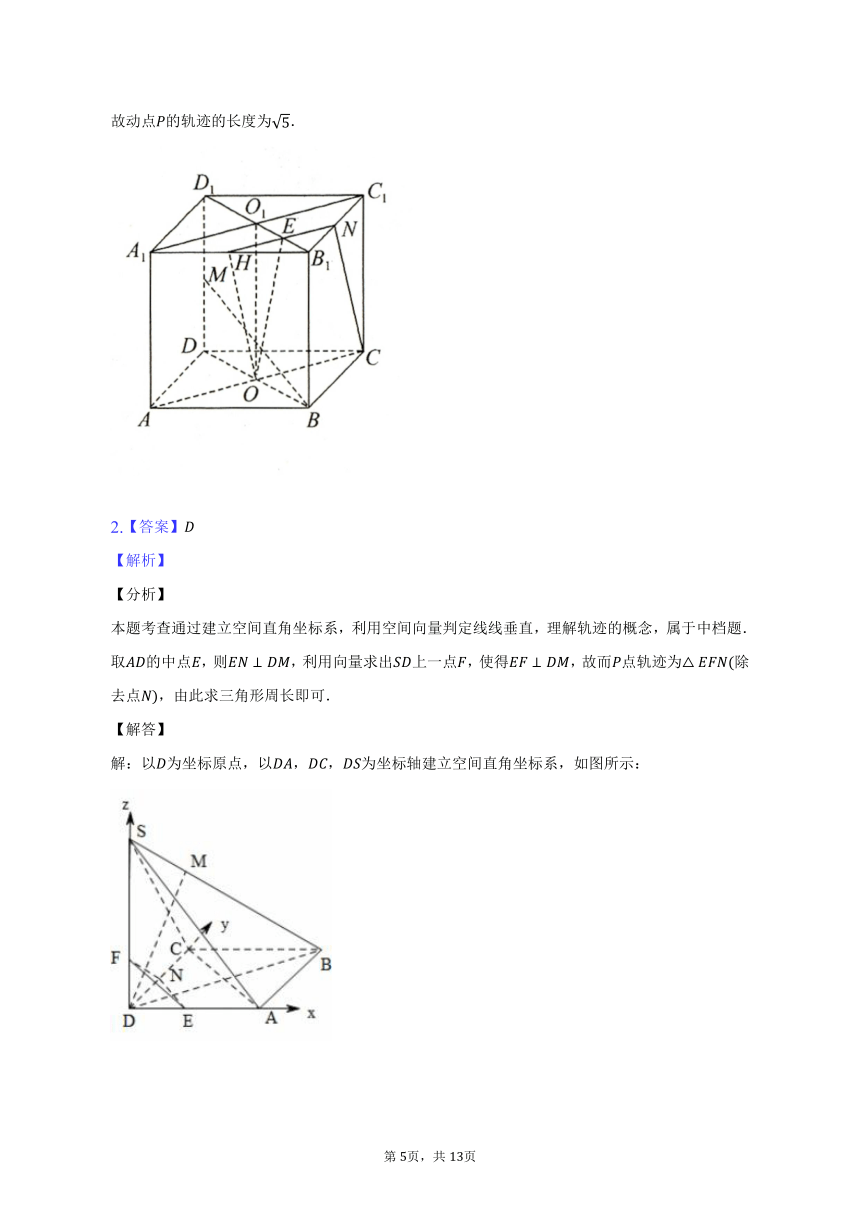
本题考查通过建立空间直角坐标系,利用空间向量判定线线垂直,理解轨迹的概念,属于中档题.
取的中点,则,利用向量求出上一点,使得,故而点轨迹为除去点,由此求三角形周长即可.
【解答】
解:以为坐标原点,以,,为坐标轴建立空间直角坐标系,如图所示:
则,,,,,
取的中点,则,
,,
,即,
在上取一点,设,则,
设,则,
即,计算得出,
又
平面,
点轨迹为除去点,
,,
的周长为,
故选D.
3.【答案】
【解析】
【分析】
本题考查了正方体的结构特征应用问题,也考查了利用向量法判定直线与平面平行,是中档题.
设点,利用向量法求出与的值,进而可得轨迹长度。
【解答】
解:根据题意,以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,
则、、、,设点,
,,设平面的法向量为,由,取,可得,
,由题意可知,平面,则,
令,可得;令,可得.
易知点的轨迹交线段于点,交线段的中点,
因此点的轨迹长度为.
4.【答案】
【解析】
【分析】
本题主要考查了立体几何中的轨迹问题,线面垂直的判定,考查学生的分析解决问题的能力,属于中档题.
取的中点,设交于点,根据线面垂直的判定可得使与垂直的点所构成的轨迹为矩形,即可得解.
【解答】
解:如图,取的中点,连接,,,设交于点,则,
平面,平面,
,
正方体的棱长为,,分别是,的中点,
,,
,
,
,即,
又,、平面,
平面,
使与垂直的点所构成的轨迹为矩形,
正方体的棱长为,
由勾股定理可得,使与垂直的点所构成的轨迹的周长等于.
故选:.
5.【答案】
【解析】
【分析】
本题以正方体为载体,考查轨迹,考查曲线的周长,属于较难题.
本题首先要弄清楚曲线的形状,再根据曲线的性质及解析几何知识即可求出长度.
【解答】
解:由题意得动点的轨迹是以为球心,
半径为的球面被平面截得的小圆上,结合正方体,所以侧面,所以为截面圆的圆心,故 B皆为截面圆的半径,易知
截面半径为,
由所以点轨迹即弧长.
故选D.
6.【答案】
【解析】
【分析】
本题考查了空间动点的轨迹,四棱锥的结构特征和面面垂直的性质,同时考查了空间想象能力,推理能力,属于中档题.
先找符合条件的特殊位置,然后根据符合条件的轨迹为线段的垂直平分面与平面的交线得到的轨迹.
【解答】
解:根据题意可知,
则点符合“为底面内的一个动点,且满足”,
设的中点为,
因为侧面底面,侧面底面,
,底面,
所以侧面,又侧面,
所以,
根据题目条件可知≌,
,点也符合“为底面内的一个动点,且满足”,
故动点的轨迹肯定过点和点,
而到点与到点的距离相等的点为线段的垂直平分面,
线段的垂直平分面与平面的交线是一直线
故选A.
7.【答案】
【解析】
【分析】
本题考查利用空间向量法解决立体几何问题,考查直观想象与数学运算的核心素养,属于拔高题.
首先可证,在上取,使得,连接,则,可得记与的交点为,以为坐标原点,建立空间直角坐标系,在上取一点,由,求出点的位置,从而得到动点轨迹,即可求出动点的轨迹围成的图形的面积,显然当与重合时,与平面所成角最大,利用空间向量法求异面直线所成角的余弦值.
【解答】
解:如图,
在直四棱柱中,因为底面是菱形,侧棱垂直底面,
所以平面,
又平面,
所以.
在上取,使得,连接,则,所以.
记与的交点为,以为坐标原点,建立如图所示的空间直角坐标系,
则,,.
在上取一点,记为,于是,.
由,得,即,
所以的边为点的运动轨迹.
由题意得,,
动点的轨迹围成的图形的面积为.
显然当与重合时,与平面所成角最大.
因为,,
所以,,
因为直线的一个方向向量为,
所以,
即异面直线与所成角的余弦值为.
故答案为:;.
8.【答案】
【解析】
【分析】
本题考查线面垂直的性质和与弧长有关的轨迹问题,属于中档题.
由题意可得平面,故DK,则,故K点在以为直径的圆上,连接交此圆于点,则圆弧就是点的轨迹,利用弧长公式求出轨迹长度.
【解答】
解:由题意,点在面上的射影在直线上,易得平面,平面,故DK,
则,故K点在以为直径的圆上,如图,连接交此圆于点,
则圆弧就是点的轨迹,设圆心为,
在长方形中,,,则易得,则,
其所对的弧长为,
故答案为:.
9.【答案】
【解析】
【分析】
本题考查空间中直线与直线的位置关系,属于中档题.
由判断出所在的平面,从而推断出点形成的轨迹长度,再用几何的知识求出即可.
【解答】
解:过点作点垂线交于点,交底面圆于点,
连接,,,
底面圆,又,,
又面,
面,面,
,又,面,
面,又面,
,,
在中得,
可得点形成的轨迹长度为.
故答案为.
10.【答案】
【解析】
【分析】
本题考查正方体的结构特征,立体几何轨迹问题,考查线线垂直的向量表示,属于中档题.
根据题意以为原点建立空间直角坐标系,由,可得,分析得点的轨迹为的长度,计算可得.
【解答】
解:如图以为原点建立空间直角坐标系,
,,,
设,其中,,
,,
,
,即,
,
即,
又,,
点的轨迹为面上的直线,所示部分,即图中的长度,
由图知,
故答案为:.
第1页,共1页
