141.6 多项式与多项式相乘 精品课件(共27张PPT)
文档属性
| 名称 | 141.6 多项式与多项式相乘 精品课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-27 18:24:39 | ||
图片预览








文档简介
(共27张PPT)
八上数学同步精品课件
人教版八年级上册
14.1.6 多项式与多项式相乘
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.理解并掌握多项式与多项式的乘法运算法则.(重点)
2.能够灵活运用多项式与多项式的乘法运算法则进行计算.(难点)
1.请说出单项式与单项式相乘的法则:
2.如何进行单项式与多项式乘法的运算?
3.进行单项式与多项式乘法运算时,要注意什么?
①不能漏乘:即单项式要乘遍多项式的每一项;②去括号时注意符号的确定.
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
计算:
(1)(3x3y) · (-2xy2); (2)(-ab3c2)3 · (-2a3b)2 ;
(3)3a(2a2-1); (4)2x(x-2)-4x(x-1).
解:(1)(3x3y) · (-2xy2)=3×(-2)×(x3 · x)(y ·y2)=-6x4y3;
(2)(-ab3c2)3 · (-2a3b)2=(-a3b9c6) · (4a6b2)=-4a9b11c6;
(3)3a(2a2-1)=6a3-3a;
(4)2x(x-2)-4x(x-1)=2x2-4x-4x2+4x=2x2-4x2-4x+4x=-2x2.
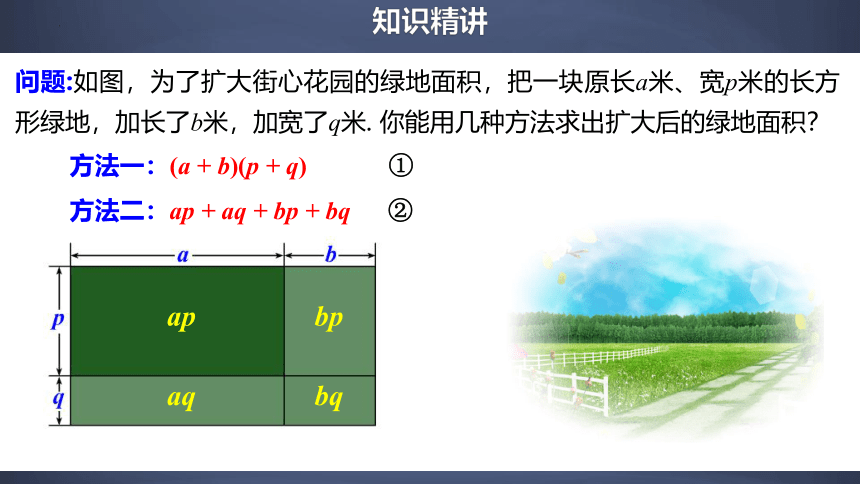
问题:如图,为了扩大街心花园的绿地面积,把一块原长a米、宽p米的长方形绿地,加长了b米,加宽了q米. 你能用几种方法求出扩大后的绿地面积?
方法一:(a + b)(p + q) ①
方法二:ap + aq + bp + bq ②
ap
bp
aq
bq
由于①②表示同一个数量,所以
(a + b)(p + q)= ap + aq + bp + bq
方法一:(a + b)(p + q) ①
方法二:ap + aq + bp + bq ②
计算(a+b)(p+q),可以先把其中的一个多项式,如p+q,看成一个整体,运用单项式与多项式相乘的法则,得
(a+b)(p+q)=a(p+q)+b(p+q)
再利用单项式与多项式相乘的法则,得
a(p+q)+b(p+q)=ap+aq+bp+bq
总体上看,(a+b)(p+q)的结果可以看作a+b的每一项乘p+q的每一项,再把所得的积相加而得到的,即
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
例1.计算:
(1) (3x+1)(x+2) (2) (x-8y)(x-y) (3) (x+y)(x2-xy+y2)
解:
(1)(3x+1)(x+2) =(3x)·x+(3x)×2+1·x+1×2=3x2+6x+x+2=3x2+7x+2
(2)(x-8y)(x-y) =x2-xy-8xy+8y2=x2-9xy+8y2
(3)(x+y)(x2-xy+y2) =x3-x2y+xy2+x2y-xy2+y3=x3+y3
【点睛】在进行多项式与多项式相乘时要注意结果中有同类项的要合并同类项;计算时要注意符号问题;不要漏乘.
计算:
(1) (2x+1)(x+3) (2) (m+2n)(3n-m) (3) (a-1)2
(4) (a+3b)(a-3b) (5) (2x2-1)(x-4) (6) (x2+2x+3)(2x-5)
解:(1)原式=2x2+6x+x+3=2x2+7x+3
(2)原式=3mn-m2+6n2-2mn=mn-m2+6n2
(3)原式=(a-1)(a-1)=a2-a-a+1=a2-2a+1
(4)原式=a2-3ab+3ab-9b2=a2-9b2
(5)原式=2x2-8x2-x+4
(6)原式=2x3-5x2+4x2-10x+6x-15=2x3-x2-4x-15
练一练:
(1)(x+2)(x+3)=__________;
(2)(x-4)(x+1)=__________;
(3)(y+4)(y-2)=__________;
(4)(y-5)(y-3)=__________.
x2+5x+6
x2-3x-4
y2+2y-8
y2-8y+15
由上面计算的结果找规律,观察填空:
(x+p)(x+q)=___2+______x+______.
x
(p+q)
pq
例2.先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b),其中a=-1,b=1.
当a=-1,b=1时,
解:原式=a3-8b3-(a2-5ab)(a+3b)
=a3-8b3-a3-3a2b+5a2b+15ab2
=-8b3+2a2b+15ab2.
原式=-8+2-15=-21.
先化简,再求值:,其中.
解:原式
,
当时,
原式.
例3.已知ax2+bx+1(a≠0)与3x-2的积不含x2项,也不含x项,求系数a、b的值.
解:(ax2+bx+1)(3x-2)
=3ax3+(-2a+3b)x2+(-2b+3)x-2.
∵积不含x2项,也不含x项,
【点睛】解决此类问题首先要利用多项式乘法法则计算出展开式,合并同类项后,再根据不含某一项,可得这一项系数等于零,再列出方程(组)解答.
若(x2+mx+8)(x2﹣3x+n)的展开式中不含x3和x2的项,求mn的值.
解:(x2+mx+8)(x2-3x+n)
=x4﹣3x3+nx2+mx3﹣3mx2+mnx+8x2﹣24x+8n
=x4+(m﹣3)x3+(n﹣3m+8)x2+(mn﹣24)x+8n,
∵展开式中不含x3和x2的项,
∴ ,
解得:m=3,n=1,
∴mn=3×1=3.
例4.小丽设计了两枚“中国梦”的邮票,第一枚的宽是m厘米,长比宽多x厘米;第二枚的宽是第一枚的长,且第二枚的长比宽多2x厘米.(1)求第一枚邮票的面积.(2)第二枚邮票比第一枚邮票的面积大多少
解:(1)m (m+x)=m2+mx
(2)(m+x) (m+3x)-(m2+mx)
=m2+3mx+mx+3x2-m2-mx=3mx+3x2
答:第一枚邮票的面积是中国邮(m2+mx)厘米2, 第二枚邮票的政面积比第一枚大(3mx+3x2)厘米2.
例5.已知等式(x+a)(x+b)= x2+mx+28,其中a、b、m均为正整数,你认为m可取哪些值?它与a、b的取值有关吗?请你写出所有满足题意的m的值.
解:由题意可得a+b=m,ab=28.
∵a、b均为正整数,故可分以下情况讨论:
①a=1,b=28或a=28,b=1,此时m=29;
②a=2,b=14或a=14,b=2,此时m=16;
③a=4,b=7或a=7,b=4,此时m=11.
综上所述,m的取值与a、b的取值有关,m的值为29或16或11.
1.计算(x+1)(x+2)的结果为( )
A.x2+2 B.x2+3x+2 C.x2+3x+3 D.x2+2x+2
2.下列多项式相乘的结果为x2+3x-18的是( )
A. (x-2)(x+9) B. (x+2)(x-9) C. (x+3)(x-6) D. (x-3)(x+6)
3.若(x+3)(x+n)=x2+mx-15,则m的值为( )
A.-5 B.5 C.-2 D.2
4.已知(x-2)(x2+mx+n)的乘积项中不含x2和x项, 则m,n的值分别为( )
A. m=2,n=4 B. m=3, n=6 C. m=-2,n=-4 D. m=-3,n=-6
B
D
C
A
5.设M=(x-3) (x-7),N=(x-2)(x-8),则M与N的关系为( )
A.MN C. M=N D.不能确定
6.通过计算比较图①、图②中阴影部分的面积,可以验证的计算式子是( )
A.a(b-x)=ab-ax B. b(a-x)=ab-bx .
C. (a-x) (b-x)=ab-ax-bx D. (a-x) (b-x)=ab-ax-bx+x2
B
D
7.计算:(1) (x+3) (x+4)=____________; (2) (x-3)(x-4)=____________;
(3) (x+3) (x-4)=_____________; (4) (x-3) (x+4)=_____________.
9.若(x-2) (x+3)=x2+ax+b, 则a=____,b=____.
9.如果a2+a=1,那么(a-5) (a+6)的值为_____.
10.通过计算几何图形的面积可表示一些代数恒等
式(一定成立的等式),请根据右图写出一个代数
恒等式是:___________________________.
x2+7x+12
x2-7x+12
x2-x-12
x2+x-12
1
-6
-29
(a+b) (2a+b) =2a2+3ab+b2
11.计算:
(2x+3y) (x -2y) (2) (-2a+3) (5+a) (3) (-3m+2)2
(4) (m+2) (2m2-m-3)
解: (1) 原式= 2x2-4xy+3xy-6y2=2x2-xy -6y2
(2)原式=-10a-2a2+15+3a=-2a2-7a+15
(3)原式= (-3m+2) (-3m+2)= 9m2-6m-6m+4= 9m2-12m+4
(4)原式= 2m3-m2-3m+4m2-2m-6= 2m3-m2+4m2-3m-2m-6= 2m3+3m2-5m-6
12.先化简,再求值: (2x-5)(3x+2)-6(x+1)(x-2),其中x=-.
解:原式=6x2+4x-15x-10-6(x2-2x+x-2)
=6x2+4x-15x-10-6x2+12x-6x+12
=6x2-6x2+4x-15x+12x-6x-10+12
=6x2-6x2+4x-15x+12x-6x-10+12
=-5x+2
当x=-时,
原式=-5×(-)+2=3.
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
八上数学同步精品课件
人教版八年级上册
14.1.6 多项式与多项式相乘
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.理解并掌握多项式与多项式的乘法运算法则.(重点)
2.能够灵活运用多项式与多项式的乘法运算法则进行计算.(难点)
1.请说出单项式与单项式相乘的法则:
2.如何进行单项式与多项式乘法的运算?
3.进行单项式与多项式乘法运算时,要注意什么?
①不能漏乘:即单项式要乘遍多项式的每一项;②去括号时注意符号的确定.
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
计算:
(1)(3x3y) · (-2xy2); (2)(-ab3c2)3 · (-2a3b)2 ;
(3)3a(2a2-1); (4)2x(x-2)-4x(x-1).
解:(1)(3x3y) · (-2xy2)=3×(-2)×(x3 · x)(y ·y2)=-6x4y3;
(2)(-ab3c2)3 · (-2a3b)2=(-a3b9c6) · (4a6b2)=-4a9b11c6;
(3)3a(2a2-1)=6a3-3a;
(4)2x(x-2)-4x(x-1)=2x2-4x-4x2+4x=2x2-4x2-4x+4x=-2x2.
问题:如图,为了扩大街心花园的绿地面积,把一块原长a米、宽p米的长方形绿地,加长了b米,加宽了q米. 你能用几种方法求出扩大后的绿地面积?
方法一:(a + b)(p + q) ①
方法二:ap + aq + bp + bq ②
ap
bp
aq
bq
由于①②表示同一个数量,所以
(a + b)(p + q)= ap + aq + bp + bq
方法一:(a + b)(p + q) ①
方法二:ap + aq + bp + bq ②
计算(a+b)(p+q),可以先把其中的一个多项式,如p+q,看成一个整体,运用单项式与多项式相乘的法则,得
(a+b)(p+q)=a(p+q)+b(p+q)
再利用单项式与多项式相乘的法则,得
a(p+q)+b(p+q)=ap+aq+bp+bq
总体上看,(a+b)(p+q)的结果可以看作a+b的每一项乘p+q的每一项,再把所得的积相加而得到的,即
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
例1.计算:
(1) (3x+1)(x+2) (2) (x-8y)(x-y) (3) (x+y)(x2-xy+y2)
解:
(1)(3x+1)(x+2) =(3x)·x+(3x)×2+1·x+1×2=3x2+6x+x+2=3x2+7x+2
(2)(x-8y)(x-y) =x2-xy-8xy+8y2=x2-9xy+8y2
(3)(x+y)(x2-xy+y2) =x3-x2y+xy2+x2y-xy2+y3=x3+y3
【点睛】在进行多项式与多项式相乘时要注意结果中有同类项的要合并同类项;计算时要注意符号问题;不要漏乘.
计算:
(1) (2x+1)(x+3) (2) (m+2n)(3n-m) (3) (a-1)2
(4) (a+3b)(a-3b) (5) (2x2-1)(x-4) (6) (x2+2x+3)(2x-5)
解:(1)原式=2x2+6x+x+3=2x2+7x+3
(2)原式=3mn-m2+6n2-2mn=mn-m2+6n2
(3)原式=(a-1)(a-1)=a2-a-a+1=a2-2a+1
(4)原式=a2-3ab+3ab-9b2=a2-9b2
(5)原式=2x2-8x2-x+4
(6)原式=2x3-5x2+4x2-10x+6x-15=2x3-x2-4x-15
练一练:
(1)(x+2)(x+3)=__________;
(2)(x-4)(x+1)=__________;
(3)(y+4)(y-2)=__________;
(4)(y-5)(y-3)=__________.
x2+5x+6
x2-3x-4
y2+2y-8
y2-8y+15
由上面计算的结果找规律,观察填空:
(x+p)(x+q)=___2+______x+______.
x
(p+q)
pq
例2.先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b),其中a=-1,b=1.
当a=-1,b=1时,
解:原式=a3-8b3-(a2-5ab)(a+3b)
=a3-8b3-a3-3a2b+5a2b+15ab2
=-8b3+2a2b+15ab2.
原式=-8+2-15=-21.
先化简,再求值:,其中.
解:原式
,
当时,
原式.
例3.已知ax2+bx+1(a≠0)与3x-2的积不含x2项,也不含x项,求系数a、b的值.
解:(ax2+bx+1)(3x-2)
=3ax3+(-2a+3b)x2+(-2b+3)x-2.
∵积不含x2项,也不含x项,
【点睛】解决此类问题首先要利用多项式乘法法则计算出展开式,合并同类项后,再根据不含某一项,可得这一项系数等于零,再列出方程(组)解答.
若(x2+mx+8)(x2﹣3x+n)的展开式中不含x3和x2的项,求mn的值.
解:(x2+mx+8)(x2-3x+n)
=x4﹣3x3+nx2+mx3﹣3mx2+mnx+8x2﹣24x+8n
=x4+(m﹣3)x3+(n﹣3m+8)x2+(mn﹣24)x+8n,
∵展开式中不含x3和x2的项,
∴ ,
解得:m=3,n=1,
∴mn=3×1=3.
例4.小丽设计了两枚“中国梦”的邮票,第一枚的宽是m厘米,长比宽多x厘米;第二枚的宽是第一枚的长,且第二枚的长比宽多2x厘米.(1)求第一枚邮票的面积.(2)第二枚邮票比第一枚邮票的面积大多少
解:(1)m (m+x)=m2+mx
(2)(m+x) (m+3x)-(m2+mx)
=m2+3mx+mx+3x2-m2-mx=3mx+3x2
答:第一枚邮票的面积是中国邮(m2+mx)厘米2, 第二枚邮票的政面积比第一枚大(3mx+3x2)厘米2.
例5.已知等式(x+a)(x+b)= x2+mx+28,其中a、b、m均为正整数,你认为m可取哪些值?它与a、b的取值有关吗?请你写出所有满足题意的m的值.
解:由题意可得a+b=m,ab=28.
∵a、b均为正整数,故可分以下情况讨论:
①a=1,b=28或a=28,b=1,此时m=29;
②a=2,b=14或a=14,b=2,此时m=16;
③a=4,b=7或a=7,b=4,此时m=11.
综上所述,m的取值与a、b的取值有关,m的值为29或16或11.
1.计算(x+1)(x+2)的结果为( )
A.x2+2 B.x2+3x+2 C.x2+3x+3 D.x2+2x+2
2.下列多项式相乘的结果为x2+3x-18的是( )
A. (x-2)(x+9) B. (x+2)(x-9) C. (x+3)(x-6) D. (x-3)(x+6)
3.若(x+3)(x+n)=x2+mx-15,则m的值为( )
A.-5 B.5 C.-2 D.2
4.已知(x-2)(x2+mx+n)的乘积项中不含x2和x项, 则m,n的值分别为( )
A. m=2,n=4 B. m=3, n=6 C. m=-2,n=-4 D. m=-3,n=-6
B
D
C
A
5.设M=(x-3) (x-7),N=(x-2)(x-8),则M与N的关系为( )
A.M
6.通过计算比较图①、图②中阴影部分的面积,可以验证的计算式子是( )
A.a(b-x)=ab-ax B. b(a-x)=ab-bx .
C. (a-x) (b-x)=ab-ax-bx D. (a-x) (b-x)=ab-ax-bx+x2
B
D
7.计算:(1) (x+3) (x+4)=____________; (2) (x-3)(x-4)=____________;
(3) (x+3) (x-4)=_____________; (4) (x-3) (x+4)=_____________.
9.若(x-2) (x+3)=x2+ax+b, 则a=____,b=____.
9.如果a2+a=1,那么(a-5) (a+6)的值为_____.
10.通过计算几何图形的面积可表示一些代数恒等
式(一定成立的等式),请根据右图写出一个代数
恒等式是:___________________________.
x2+7x+12
x2-7x+12
x2-x-12
x2+x-12
1
-6
-29
(a+b) (2a+b) =2a2+3ab+b2
11.计算:
(2x+3y) (x -2y) (2) (-2a+3) (5+a) (3) (-3m+2)2
(4) (m+2) (2m2-m-3)
解: (1) 原式= 2x2-4xy+3xy-6y2=2x2-xy -6y2
(2)原式=-10a-2a2+15+3a=-2a2-7a+15
(3)原式= (-3m+2) (-3m+2)= 9m2-6m-6m+4= 9m2-12m+4
(4)原式= 2m3-m2-3m+4m2-2m-6= 2m3-m2+4m2-3m-2m-6= 2m3+3m2-5m-6
12.先化简,再求值: (2x-5)(3x+2)-6(x+1)(x-2),其中x=-.
解:原式=6x2+4x-15x-10-6(x2-2x+x-2)
=6x2+4x-15x-10-6x2+12x-6x+12
=6x2-6x2+4x-15x+12x-6x-10+12
=6x2-6x2+4x-15x+12x-6x-10+12
=-5x+2
当x=-时,
原式=-5×(-)+2=3.
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
