14.2.2 完全平方公式 精品课件(共34张PPT)
文档属性
| 名称 | 14.2.2 完全平方公式 精品课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-27 18:39:18 | ||
图片预览











文档简介
(共34张PPT)
八上数学同步精品课件
人教版八年级上册
14.2.2 完全平方公式
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.理解并掌握完全平方公式的推导过程、结构特点、几何解释.(重点)
2.灵活应用完全平方公式进行计算.(难点)
一块边长为a米的正方形实验田,因其边长增加b米,形成四块实验田,以种植不同的新品种.
你能用不同的方法表示试验田的总面积吗?
①总面积=(a+b)2
②总面积=a2+ab+ab+b2
=a2+2ab+b2
ab
b2
a2
ab
你发现了什么?
(a+b)2=a2+2ab+b2
计算下列各式,你能发现什么规律?
(1) (p+1)2=(p+1)(p+1)=_________;(2) (m+2)2=_________;
(3) (p-1)2=(p-1)(p-1)=_________;(4) (m-2)2=_________.
p2+2p+1
m2+4m+4
P2-2p+1
m2-4m+4
计算:(a+b)2,(a-b)2.
(a+b)2=(a+b)(a+b) =a2+ab+ab+b2=a2+2ab+b2
(a-b)2=(a-b)(a-b) =a2-ab-ab+b2=a2-2ab+b2
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
可以合写成 (a±b)2=a2±2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
注:公式中的字母a、b可以表示数、单项式和多项式.
(简记为:“首平方,尾平方,积的2倍中间放”)
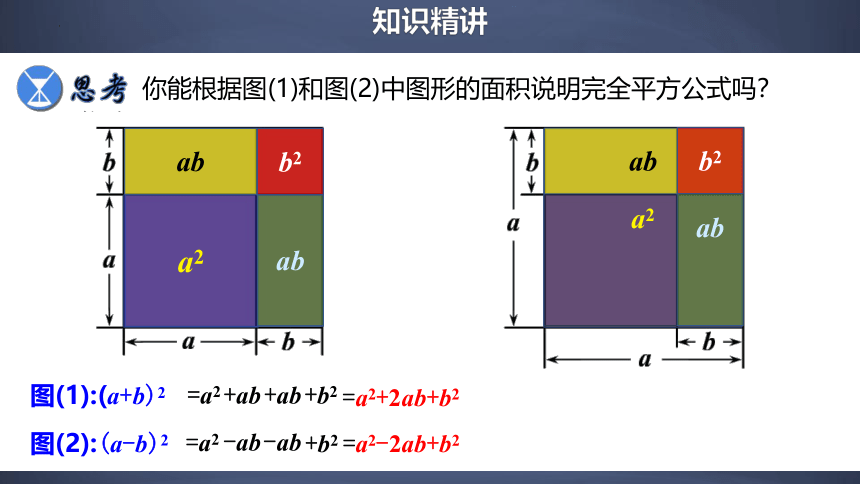
你能根据图(1)和图(2)中图形的面积说明完全平方公式吗?
图(1):(a+b)2
=a2
图(2):(a-b)2
+ab
+ab
+b2
a2
ab
ab
b2
=a2+2ab+b2
=a2
=a2-2ab+b2
-ab
+b2
-ab
a2
ab
ab
b2
(a+b)2= a2+2ab+b2.
(a-b)2= a2-2ab+b2.
观察下面两个完全平方式,比一比,回答下列问题:
1.说一说积的次数和项数;
2.两个完全平方式的积有相同的项吗?与a,b有什么关系?
3.两个完全平方式的积中不同的是哪一项?与a,b有什么关系?它的符号与什么有关?
公式特征:
4.公式中的字母a,b可以表示数,单项式和多项式.
1.积为二次三项式;
2.积中两项为两数的平方和;
3.另一项是两数积的2倍,且与两数中间的符号相同;
(a+b)2= a2+2ab+b2.
(a-b)2= a2-2ab+b2.
例1.运用完全平方公式计算:
(1) (4m+n)2 (2)
解:(1)(4m+n)2
=(4m)2+2 (4m) n+n2
=16m2+8mn+n2
解:(2)
=y2-2 y +()2
=y2-y+
运用完全平方公式计算:
(1) (x+6)2 (2) (y-5)2 (3) (-2x+5)2 (4)
解:(1)原式= x2+2·x·6+62 = x2+12x+36
(2)原式= y2-2·y·5+52 = y2-10y+25
(3)原式=(5-2x)2 = 52-2·5·2x+(2x)2 = 25-20x+4x2
(4)原式=
例2.运用完全平方公式计算:
(1) 1022 (2) 992
解:(1) 1022=(100+2)2
=1002+2×100×2+22
=10000+400+4
=10404
解:(2) 992=(100-1)2
=1002-2×100×1+12
=10000-200+1
=9801
利用完全平方公式简便计算:
(1); (2).
(1)解:原式=
=
=
= ;
(2)解:原式=
=
=
(a+b)2与(-a-b)2相等吗?(a-b)2与(b-a)2相等吗?(a-b)2与a2-b2相等吗?为什么?
(-a-b)2=(-a)2-2·(-a)·b+b2
只有当b=0或a=b时,(a-b)2=a2-b2.
=a2+2ab+b2=(a+b)2
(b-a)2=b2-2ba+a2
=a2-2ab+b2=(a-b)2
(a-b)2与a2-b2不一定相等.
例3.计算:
(1)(2) .
(1)解:原式=
;
(2)解:原式=
=
计算:
(1) (2)2(x﹣1)2 ﹣x(x﹣2)+(3x﹣2)(3x+2).
(1)解原式=
=
=;
(2)解原式=
=10x2﹣2x﹣2.
例4.化简求值:已知,求代数式的值.
解:∵,
∴,
原式=
,
∵,
∴原式.
例5.若是完全平方式,则m的值为( )
A.8 B. C.4 D.
【分析】解:∵,
∴,
∴.
故选:D
D
例6.(1)已知,,求①的值;②的值;
(2)已知,求的值.
解:(1)①,,
,
.
②,
.
例6.(1)已知,,求①的值;②的值;
(2)已知,求的值.
解:(2),且,
,
,
,
.
1.计算: (1) (a+5)2=_________;(2) 1012=________.
2.若(3x+a)2=9x2+bx+4,则a+b的值为_______.
3.将4个数a, b,c, d排成2行2列,两边各加一条坚直线记为 ,定义 ,上述记号就叫做2阶行列式.若 ,则x=_____.
a2+10a+25
10201
±14
3
4.下列计算正确的是( )
A. B.
C. D.
5.计算的结果是( )
A. B. C. D.
6.计算:( )
A.﹣2000 B.﹣1995 C.2000 D.1995
B
B
B
7.若,则的值为( )
A.26 B.24 C.20 D.28
8.如果是一个完全平方式,那么k的值是( )
A.4 B.±8 C.8 D.±4
9.已知,则等于( )
A. B. C. D.
D
B
B
10.先化简,再求值:,其中,b=2.
解原式
,
将,b=2代入,
原式.
11.已知,求:
(1)xy的值;
(2)的值.
(1)解:因为
可得:;
(2)因为,
可得:.
12.如图,某市修建了一个大正方形休闲场所,在大正方形内规划了一个正方形活动区,连接绿地到大正方形四边的笔直小路如图所示.已知大正方形休闲场所的边长为6a米,四条小路的长与宽都为b米和米.阴影区域铺设草坪,草坪的造价为每平米30元.
(1)用含a、b的代数式表示草坪(阴影)面积并化简.
(2)若a=6,b=6,计算草坪的造价.
(1)解:根据题意得:阴影部分的面积为:大正方形的面积减去4个长方形的面积再减去中间小正方形的面积,
∴草坪(阴影)面积为:
平方米;
12.如图,某市修建了一个大正方形休闲场所,在大正方形内规划了一个正方形活动区,连接绿地到大正方形四边的笔直小路如图所示.已知大正方形休闲场所的边长为6a米,四条小路的长与宽都为b米和米.阴影区域铺设草坪,草坪的造价为每平米30元.
(1)用含a、b的代数式表示草坪(阴影)面积并化简.
(2)若a=6,b=6,计算草坪的造价.
(2)解:草坪的造价为:
元.
13.若,求m,n的值.
解:∵,
∴( )=0,
即( )+( )=0.
根据非负数的性质,得m=n= .
(1)阅读上述解答过程,并补充横线处的内容;
(2)设等腰三角形ABC的三边长分别为a,b,c,且满足,求△ABC的周长.
(1)解:完善例题的解题过程:
∵,
∴,
即,
∴m=n=4;
(2)设等腰三角形ABC的三边长分别为a,b,c,且满足,求△ABC的周长.
(2)解:∵,
∴,
∴,
∴a 2=0且b 3=0,
∴a=2,b=3,
∵等腰△ABC的三边长为:a、b、c,
∴当c=a时,三边分别为:2、2、3,此时能围成三角形,△ABC的周长=2+2+3=7;
当c=b时,三边分别为:2、3、3,此时能围成三角形,△ABC的周长=2+3+3=8;
综上所述,等腰△ABC的周长为7或8.
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
可以合写成 (a±b)2=a2±2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
注:公式中的字母a、b可以表示数、单项式和多项式.
(简记为:“首平方,尾平方,积的2倍中间放”)
公式特征:
4.公式中的字母a,b可以表示数,单项式和多项式.
1.积为二次三项式;
2.积中两项为两数的平方和;
3.另一项是两数积的2倍,且与两数中间的符号相同;
(a+b)2= a2+2ab+b2.
(a-b)2= a2-2ab+b2.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
八上数学同步精品课件
人教版八年级上册
14.2.2 完全平方公式
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.理解并掌握完全平方公式的推导过程、结构特点、几何解释.(重点)
2.灵活应用完全平方公式进行计算.(难点)
一块边长为a米的正方形实验田,因其边长增加b米,形成四块实验田,以种植不同的新品种.
你能用不同的方法表示试验田的总面积吗?
①总面积=(a+b)2
②总面积=a2+ab+ab+b2
=a2+2ab+b2
ab
b2
a2
ab
你发现了什么?
(a+b)2=a2+2ab+b2
计算下列各式,你能发现什么规律?
(1) (p+1)2=(p+1)(p+1)=_________;(2) (m+2)2=_________;
(3) (p-1)2=(p-1)(p-1)=_________;(4) (m-2)2=_________.
p2+2p+1
m2+4m+4
P2-2p+1
m2-4m+4
计算:(a+b)2,(a-b)2.
(a+b)2=(a+b)(a+b) =a2+ab+ab+b2=a2+2ab+b2
(a-b)2=(a-b)(a-b) =a2-ab-ab+b2=a2-2ab+b2
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
可以合写成 (a±b)2=a2±2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
注:公式中的字母a、b可以表示数、单项式和多项式.
(简记为:“首平方,尾平方,积的2倍中间放”)
你能根据图(1)和图(2)中图形的面积说明完全平方公式吗?
图(1):(a+b)2
=a2
图(2):(a-b)2
+ab
+ab
+b2
a2
ab
ab
b2
=a2+2ab+b2
=a2
=a2-2ab+b2
-ab
+b2
-ab
a2
ab
ab
b2
(a+b)2= a2+2ab+b2.
(a-b)2= a2-2ab+b2.
观察下面两个完全平方式,比一比,回答下列问题:
1.说一说积的次数和项数;
2.两个完全平方式的积有相同的项吗?与a,b有什么关系?
3.两个完全平方式的积中不同的是哪一项?与a,b有什么关系?它的符号与什么有关?
公式特征:
4.公式中的字母a,b可以表示数,单项式和多项式.
1.积为二次三项式;
2.积中两项为两数的平方和;
3.另一项是两数积的2倍,且与两数中间的符号相同;
(a+b)2= a2+2ab+b2.
(a-b)2= a2-2ab+b2.
例1.运用完全平方公式计算:
(1) (4m+n)2 (2)
解:(1)(4m+n)2
=(4m)2+2 (4m) n+n2
=16m2+8mn+n2
解:(2)
=y2-2 y +()2
=y2-y+
运用完全平方公式计算:
(1) (x+6)2 (2) (y-5)2 (3) (-2x+5)2 (4)
解:(1)原式= x2+2·x·6+62 = x2+12x+36
(2)原式= y2-2·y·5+52 = y2-10y+25
(3)原式=(5-2x)2 = 52-2·5·2x+(2x)2 = 25-20x+4x2
(4)原式=
例2.运用完全平方公式计算:
(1) 1022 (2) 992
解:(1) 1022=(100+2)2
=1002+2×100×2+22
=10000+400+4
=10404
解:(2) 992=(100-1)2
=1002-2×100×1+12
=10000-200+1
=9801
利用完全平方公式简便计算:
(1); (2).
(1)解:原式=
=
=
= ;
(2)解:原式=
=
=
(a+b)2与(-a-b)2相等吗?(a-b)2与(b-a)2相等吗?(a-b)2与a2-b2相等吗?为什么?
(-a-b)2=(-a)2-2·(-a)·b+b2
只有当b=0或a=b时,(a-b)2=a2-b2.
=a2+2ab+b2=(a+b)2
(b-a)2=b2-2ba+a2
=a2-2ab+b2=(a-b)2
(a-b)2与a2-b2不一定相等.
例3.计算:
(1)(2) .
(1)解:原式=
;
(2)解:原式=
=
计算:
(1) (2)2(x﹣1)2 ﹣x(x﹣2)+(3x﹣2)(3x+2).
(1)解原式=
=
=;
(2)解原式=
=10x2﹣2x﹣2.
例4.化简求值:已知,求代数式的值.
解:∵,
∴,
原式=
,
∵,
∴原式.
例5.若是完全平方式,则m的值为( )
A.8 B. C.4 D.
【分析】解:∵,
∴,
∴.
故选:D
D
例6.(1)已知,,求①的值;②的值;
(2)已知,求的值.
解:(1)①,,
,
.
②,
.
例6.(1)已知,,求①的值;②的值;
(2)已知,求的值.
解:(2),且,
,
,
,
.
1.计算: (1) (a+5)2=_________;(2) 1012=________.
2.若(3x+a)2=9x2+bx+4,则a+b的值为_______.
3.将4个数a, b,c, d排成2行2列,两边各加一条坚直线记为 ,定义 ,上述记号就叫做2阶行列式.若 ,则x=_____.
a2+10a+25
10201
±14
3
4.下列计算正确的是( )
A. B.
C. D.
5.计算的结果是( )
A. B. C. D.
6.计算:( )
A.﹣2000 B.﹣1995 C.2000 D.1995
B
B
B
7.若,则的值为( )
A.26 B.24 C.20 D.28
8.如果是一个完全平方式,那么k的值是( )
A.4 B.±8 C.8 D.±4
9.已知,则等于( )
A. B. C. D.
D
B
B
10.先化简,再求值:,其中,b=2.
解原式
,
将,b=2代入,
原式.
11.已知,求:
(1)xy的值;
(2)的值.
(1)解:因为
可得:;
(2)因为,
可得:.
12.如图,某市修建了一个大正方形休闲场所,在大正方形内规划了一个正方形活动区,连接绿地到大正方形四边的笔直小路如图所示.已知大正方形休闲场所的边长为6a米,四条小路的长与宽都为b米和米.阴影区域铺设草坪,草坪的造价为每平米30元.
(1)用含a、b的代数式表示草坪(阴影)面积并化简.
(2)若a=6,b=6,计算草坪的造价.
(1)解:根据题意得:阴影部分的面积为:大正方形的面积减去4个长方形的面积再减去中间小正方形的面积,
∴草坪(阴影)面积为:
平方米;
12.如图,某市修建了一个大正方形休闲场所,在大正方形内规划了一个正方形活动区,连接绿地到大正方形四边的笔直小路如图所示.已知大正方形休闲场所的边长为6a米,四条小路的长与宽都为b米和米.阴影区域铺设草坪,草坪的造价为每平米30元.
(1)用含a、b的代数式表示草坪(阴影)面积并化简.
(2)若a=6,b=6,计算草坪的造价.
(2)解:草坪的造价为:
元.
13.若,求m,n的值.
解:∵,
∴( )=0,
即( )+( )=0.
根据非负数的性质,得m=n= .
(1)阅读上述解答过程,并补充横线处的内容;
(2)设等腰三角形ABC的三边长分别为a,b,c,且满足,求△ABC的周长.
(1)解:完善例题的解题过程:
∵,
∴,
即,
∴m=n=4;
(2)设等腰三角形ABC的三边长分别为a,b,c,且满足,求△ABC的周长.
(2)解:∵,
∴,
∴,
∴a 2=0且b 3=0,
∴a=2,b=3,
∵等腰△ABC的三边长为:a、b、c,
∴当c=a时,三边分别为:2、2、3,此时能围成三角形,△ABC的周长=2+2+3=7;
当c=b时,三边分别为:2、3、3,此时能围成三角形,△ABC的周长=2+3+3=8;
综上所述,等腰△ABC的周长为7或8.
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
可以合写成 (a±b)2=a2±2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
注:公式中的字母a、b可以表示数、单项式和多项式.
(简记为:“首平方,尾平方,积的2倍中间放”)
公式特征:
4.公式中的字母a,b可以表示数,单项式和多项式.
1.积为二次三项式;
2.积中两项为两数的平方和;
3.另一项是两数积的2倍,且与两数中间的符号相同;
(a+b)2= a2+2ab+b2.
(a-b)2= a2-2ab+b2.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
