第14章 整式的乘除与因式分解章节复习 精品课件(共65张PPT)
文档属性
| 名称 | 第14章 整式的乘除与因式分解章节复习 精品课件(共65张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-27 18:49:18 | ||
图片预览











文档简介
(共65张PPT)
八上数学同步精品课件
人教版八年级上册
14.4整式的乘除与因式分解章节复习
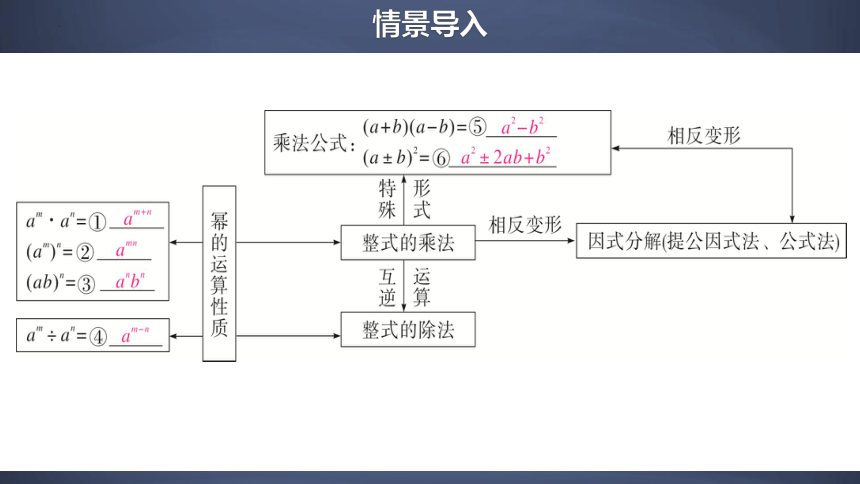
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.梳理本章的知识,并会归纳总结;
2.熟练地运用法则进行整式的乘除运算;
3.熟练地运用平方差公式和完全平方公式;
4.会对一个多项式进行因式分解.
一、幂的乘法运算
同底数幂乘法法则:
am an=______.(m,n都是正整数) 即:同底数幂相乘,底数_____,指数_____.
条件:
结果:
am+n
不变
相加
①底数不变
①乘法
②同底数幂
②指数相加
拓展:当三个或三个以上同底数幂相乘时,
am·an·ap=______.(m,n,p都是正整数)
am+n+p
一、幂的乘法运算
幂的乘方法则:
(am)n=______.(m,n都是正整数) 即:幂的乘方,底数_____,指数_____.
amn
不变
相乘
拓展:[(am)n]p = amnp (m,n,p都是正整数)
n为偶数,
n为奇数.
幂的乘方法则的逆用:
amn = (am)n
= (an)m
一、幂的乘法运算
积的乘方法则:
(ab)n=______.(n为正整数) 即:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
anbn
拓展:(abc)n=anbncn.
积的乘方公式的逆用:
anbn=(ab)n
二、整式的乘法
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
【三步走】
(1)系数相乘;
(2)相同字母的幂相乘;
(3)其余字母连同它的指数不变,作为积的因式.
二、整式的乘法
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
注:积的项数与多项式的项数相同.
单项式与多项式相乘
单项式与单项式相乘
乘法分配律
转化
二、整式的乘法
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
三、整式的除法
同底数幂的除法法则:
am÷an=am-n(a≠0,m,n都是正整数,并且m>n)即 同底数幂相除,底数_____,指数_____.
不变
相减
规定:a0=1(a≠0) 这就是说,任何不等于0的数的0次幂都等于1.
三、整式的除法
单项式相除,把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
四、乘法公式
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,等于这两个数的平方差.
公式变形:
1.(a – b ) ( a + b) = a2 - b2
2.(b + a )( -b + a ) = a2 - b2
四、乘法公式
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
可以合写成 (a±b)2=a2±2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
注:公式中的字母a、b可以表示数、单项式和多项式.
(简记为:“首平方,尾平方,积的2倍中间放”)
四、乘法公式
1.添括号与去括号是互逆的,符号的变化是一致的. 添括号是否正确可用去括号检验.
2.不论怎样添括号,原式的值都不能改变,添括号法则在利用乘法公式的计算中应用较多.
五、因式分解
我们把一个多项式化成了几个整式的积的形式,像这样的式子变形叫做这个多项式的因式分解,也叫做把这个多项式分解因式.
因式分解与整式乘法是方向相反的变形,即
因式分解
整式乘法
五、因式分解
正确找出多项式的公因式的步骤:
1.定系数:公因式的系数是多项式各项系数的最大公约数.
2.定字母:字母取多项式各项中都有的相同的字母.
3.定指数:相同字母的指数取各项中最小的一个,即字母的最低次数.
多项式各项都含有的相同因式,叫做这个多项式各项的公因式.
如:pa+pb+pc的公因式是p.
五、因式分解
如果多项式的各项有公因式,可以把这个公因式提出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
五、因式分解
例1.计算:
(1)(a+b)2·(a+b)3 (2)(m-n)3·(m-n)2·(m-n)6 (3)(x-y)2·(y-x)5
解:(1)(a+b)2·(a+b)3 =(a+b)2+3 =(a+b)5
(2)(m-n)3·(m-n)2·(m-n)6 =(m-n)3+2+6 =(m-n)11
(3)(x-y)2·(y-x)5 =(y-x)2·(y-x)5 =(y-x)2+5 =(y-x)7
【点睛】公式am·an=am+n中的底数a不仅可以代表数、单项式,还可以代表多项式等其他代数式.当底数互为相反数的幂相乘时,先把底数统一,再进行计算.
n为偶数,
n为奇数.
同底数幂的乘法及其逆用
1
例2. (1)若xa=3,xb=4,xc=5,求2xa+b+c的值;
(2)已知23x+2=32,求x的值.
(2)∵ 23x+2=32=25,
∴3x+2=5,
∴x=1.
解:(1) 2xa+b+c=2xa·xb·xc=120;
【点睛】(1)关键是逆用同底数幂的乘法公式,将所求代数式转化为几个已知因式的乘积的形式,然后再求值.
(2)关键是将等式两边转化为底数相同的形式,然后根据指数相等列方程解答.
【1-1】计算:(1) x4·x6=____;(2) a·a4=_____;
(3)5×54×53=______;(4) x2n+1·x3n-1=______.
【1-2】若am=3,an=5,则am+n等于( )
A.243 B.125 C.8 D.15
x10
a5
58
x5n
D
【1-3】计算下列各题:
(4)-a3·(-a)2·(-a)3.
(2)(a-b)3·(b-a)4;
(3) (-3)×(-3)2 ×(-3)3;
(1)(2a+b)2n+1·(2a+b)3;
解:(1)(2a+b)2n+1·(2a+b)3=(2a+b)2n+4;
(2)(a-b)3·(b-a)4=(a-b)7;
(3) (-3)×(-3)2 ×(-3)3=36;
(4)-a3·(-a)2·(-a)3=a8.
幂的乘方及其逆用
2
例3.计算:
(1) (x4)3·x6;
(2) a2(-a)2(-a2)3+a10.
解: (1) (x4)3·x6 =x12·x6= x18;
(2) a2(-a)2(-a2)3+a10
= -a2·a2·a6+a10
= -a10+a10
= 0
【点睛】与幂的乘方有关的混合运算中,一般先算幂的乘方,再算同底数幂的乘法,最后算加减,然后合并同类项.
例4.已知10m=3,10n=2,求下列各式的值.
(1)103m; (2)102n; (3)103m+2n.
解:(1)103m=(10m)3=33=27;
(2)102n=(10n)2=22=4;
(3)103m+2n=103m×102n=(10m)3× (10n)2 =27×4=108.
【点睛】此类题的关键是逆用幂的乘方及同底数幂的乘法公式,将所求代数式正确变形,然后代入已知条件求值即可.
例5.比较3500,4400,5300的大小.
分析:这三个幂的底数不同,指数也不相同,不能直接比较大小,通过观察,发现指数都是100的倍数,故可以考虑逆用幂的乘方法则.
解:3500=(35)100=243100,4400=(44)100=256100,5300=(53)100=125100.
∵256>243>125,
∴4400>3500>5300.
【点睛】比较底数大于1的幂的大小的方法有两种:(1)底数相同,指数越大,幂就越大;(2)指数相同,底数越大,幂就越大.故在此类题中,一般先观察题目所给数据的特点,将其转化为同底数的幂或同指数的幂,然后再进行大小比较.
【2-1】下列计算正确的是( )
A.a3·a2=a6 B.(a3)2=a5 C.(a2)3=a6 D.a2+a3=a5
【2-2】若,则等于( )
A. B. C. D.
【2-3】已知,,,,则 a、b、c的大小关系是( )
A.b>c>a B.a>b>c C.c>a>b D.aC
D
A
【2-4】计算:
(1); (2); (3); (4).
解:(1)
(2)
(3)
(4)
积的乘方及其逆用
3
例6.计算:
(1)(-4ab)3; (2)(-3ab2c3)3; (3)(-xmy3n)2.
解:
(1)(-4ab)3=(-4)3·a3·b3=-64a3b3
(2)(-3ab2c3)3=(-3)3·a3·(b2)3·(c3)3=-27a3b6c9
(3)(-xmy3n)2=(-1)2·(xm)2·(y3n)2=x2my6n
例7.计算:(1)0.22022×52022; (2)
解:(1)0.22022×52022
=(0.2×5)2022
=12022
=1
解:(2)
【点睛】逆用积的乘方公式an·bn=(ab)n,要灵活运用,对于不符合公式的形式,要通过恒等变形,转化为公式的形式,再运用此公式可进行简便运算.
【3-1】若(2ambm+n)3=8a9b15成立,则( )
m=3,n=2 B. m=n=3 C.m=6,n=2 D.m=3,n=5
【3-2】现规定一种新的运算“※”:a※b=ba,如3※2=23=8,则2※(-5)
=______,3※(-2x3y4)=__________.
A
25
-8x9y12
【3-3】计算:
(1)(2)
(1)解原式
(2)解原式
整式的乘法
4
例8.计算:
(2x)3(-5xy2); (2) 3x2y2 (-2xy2z)2 ; (3) (x3y)(-3xy2)3(x)2.
解:(1) (2x)3(-5xy2) =8x3(-5xy2)= [8×(-5)](x3·x)·y2=-40x4y2
(2)
(3)
例9.若与的积与是同类项,求m、n.
解:∵ ,
又∵与的积与是同类项,
∴
解得:m=2,n=3.
【点睛】单项式乘单项式就是把它们的系数和同底数幂分别相乘,结合同类项的定义,列出二元一次方程组求出参数的值,然后代入求值即可.
例10.计算:
(1); (2) [xy(x2﹣xy)﹣x2y(x﹣y)] 3xy2
解:
.
解:[xy(x2﹣xy)﹣x2y(x﹣y)] 3xy2
=(x3y﹣x2y2﹣x3y+x2y2) 3xy2
=0.
例11.先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b),其中a=-1,b=1.
当a=-1,b=1时,
解:原式=a3-8b3-(a2-5ab)(a+3b)
=a3-8b3-a3-3a2b+5a2b+15ab2
=-8b3+2a2b+15ab2.
原式=-8+2-15=-21.
例12.已知ax2+bx+1(a≠0)与3x-2的积不含x2项,也不含x项,求系数a、b的值.
解:(ax2+bx+1)(3x-2)
=3ax3+(-2a+3b)x2+(-2b+3)x-2.
∵积不含x2项,也不含x项,
【点睛】解决此类问题首先要利用多项式乘法法则计算出展开式,合并同类项后,再根据不含某一项,可得这一项系数等于零,再列出方程(组)解答.
【4-1】计算2x(3x2+1),正确的结果是( )
A.5x3+2x B.6x3+1 C.6x3+2x D.6x2+2x
【4-2】在一次数学课.上,学习了单项式乘多项式.小明回家后拿出课堂笔记本复习,发现这样一道题: -3x(-2x2+3x-1)=6x3+□+3x,“□”的地方被墨水污染了,你认为“□”内应填写( )
A.9x2 B.-9x2 C.9x D.-9x
【4-3】要使6x3(x2+ax+1)的展开式中不含x4项,则a应等于( )
A.-6 B. -1 C. D.0
C
B
D
【4-4】计算:
(2x+3y) (x -2y) (2) (-2a+3) (5+a) (3) (-3m+2)2
(4) (m+2) (2m2-m-3)
解: (1) 原式= 2x2-4xy+3xy-6y2=2x2-xy -6y2
(2)原式=-10a-2a2+15+3a=-2a2-7a+15
(3)原式= (-3m+2) (-3m+2)= 9m2-6m-6m+4= 9m2-12m+4
(4)原式= 2m3-m2-3m+4m2-2m-6= 2m3-m2+4m2-3m-2m-6= 2m3+3m2-5m-6
同底数幂的除法及其逆用
5
例13.计算:
(1)(-xy)13÷(-xy)8;(2)(x-2y)3÷(2y-x)2;(3)(a2+1)6÷(a2+1)4÷(a2+1)2.
(3)原式=(a2+1)6-4-2=(a2+1)0=1.
解:(1)原式=(-xy)13-8=(-xy)5=-x5y5;
(2)原式=(x-2y)3÷(x-2y)2=x-2y;
例14. 已知am=12,an=2,a=3,求am-n-1的值.
【点睛】解此题的关键是逆用同底数幂的除法即am-n =am÷an,对am-n-1进行变形,再代入数值进行计算.
解:∵am=12,an=2,a=3,
∴am-n-1=am÷an÷a=12÷2÷3=2.
【5-1】a12 ÷ a5=_____,(ab)3 ÷ (ab)2=_____.
(a+b)6÷(a+b)2=______,(a-c)8÷ (c-a)2=______.
【5-2】若2m=15,2n=5,则2m-n的值是_____.
a7
ab
(a-c)6
3
【5-3】计算:
(1) x7÷x5 (2) m8÷m8 (3) (-a)10÷(-a)7 (4) (xy)5÷(xy)3
解:(1) x7÷x5=x7-5=x2
(2) m8÷m8=m8-8=m0=1
(3) (-a)10÷(-a)7=(-a)10-7=(-a)3=-a3
(4) (xy)5÷(xy)3=(xy)5-3=(xy)2=x2y2
(a+b)4
整式的除法
6
例15.计算:
(12a3-6a2+3a)÷3a ; (2) (6x3y4z-4x2y3z+2xy3)÷2xy3.
解:(1)原式=12a3÷3a-6a2÷3a+3a÷3a
=4a2-2a+1;
(2)原式=6x3y4z÷2xy3-4x2y3z÷2xy3+2xy3÷2xy3
=3x2yz-2xz+1.
例16.先化简,后求值:[2x(x2y-xy2)+xy(xy-x2)]÷x2y,其中x=2022,y=2021.
解:原式=(2x3y-2x2y2+x2y2-x3y)÷x2y
原式=x-y=2022-2021=1.
=x-y.
把x=2022,y=2021代入上式,得
【6-1】(16x3-8x2+____ ) ÷ (-2x)=-8x2+4x-2
【6-2】若某长方形的面积为4a2-6ab+2a,它的长为2a,则它的宽是_________.
4x
2a-3b+1
解:(1)原式=6ab÷a+5a÷a=6b+5;
(2)原式=15x2y÷5xy-10xy2÷5xy=3x-2y;
(3)原式=72x3y4÷(-9xy2)+(-36x2y3)÷(-9xy2)+9xy2÷(-9xy2)
=-8x2y2+4xy-1.
【6-3】计算:
(6ab+5a)÷a ; (2)(15x2y-10xy2)÷5xy; (3)(72x3y4-36x2y3+9xy2)÷(-9xy2).
乘法公式的运用
7
例17.计算:
(1)(2) .
(1)解:原式=
;
(2)解:原式=
=
例18.运用乘法公式计算:
(1) (x+2y-3)(x-2y+3) (2) (a+b+c)2
解:(1) (x+2y-3)(x-2y+3)
=[(x+(2y-3)][(x-(2y-3)]
=x2-(2y-3)2
=x2-(4y2-12y+9)
=x2-4y2+12y-9
(2) (a+b+c)2
=[(a+b)+c]2
=(a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc
【点睛】第1小题选用平方差公式进行计算,需要分组.分组方法是“符号相同的为一组,符号相反的为另一组”.第2小题要把其中两项看成一个整体,再按照完全平方公式进行计算.
例19.化简求值:已知,求代数式的值.
解:∵,
∴,
原式=
,
∵,
∴原式.
例20.(1)已知,,求①的值;②的值;
(2)已知,求的值.
解:(1)①,,
,
.
②,
.
例20.(1)已知,,求①的值;②的值;
(2)已知,求的值.
解:(2),且,
,
,
,
.
【7-1】下列计算正确的是( )
A. B.
C. D.
【7-2】计算:( )
A.﹣2000 B.﹣1995 C.2000 D.1995
【7-3】(2+1)(22+1)(24+1)…(216+1)的结果为( )
A.232-1 B.232+1 C.232 D.216
B
B
A
【7-4】计算:
(1) (2)2(x﹣1)2 ﹣x(x﹣2)+(3x﹣2)(3x+2).
(1)解原式=
=
=;
(2)解原式=
=10x2﹣2x﹣2.
【7-5】运用乘法公式计算:
(1) (x-3y+1)2 (2) (3a+b-c) (3a-b+c) (3) 29×31×(302+1)
(3)原式=(30-1) × (30+1) × (302+1)
= (302-1) × (302+1)
= (302)2-12
=9002-1
=810000-1
=809999
【7-6】先化简,再求值:,其中,b=2.
解原式
,
将,b=2代入,
原式.
因式分解及应用
8
例21.下列由左边到右边的变形,属于因式分解的是( )
A. B.
C. D.
【分析】解:A.由左边到右边的变形属于因式分解,故本选项符合题意;
B.,原式等式两边不相等,即从等式的左边到右边的变形不属于因式分解,故本选项不符合题意;
C.从等式的左边到右边的变形不属于因式分解,故本选项不符合题意;
D.从等式的左边到右边的变形属于整式乘法,不属于因式分解,故本选项不符合题意;
故选:A.
A
【点睛】因式分解与整式乘法是相反方向的变形,即互逆运算,二者是一个式子的不同表现形式.因式分解的右边是两个或几个因式积的形式,整式乘法的右边是多项式的形式.
例22.已知是完全平方式,则m的值为( )
A.8 B. C.24 D.
【分析】解:∵是一个完全平方式,
∴mx=±2 2x 6,
解得:m=±24,
故选:D.
D
【点睛】本题要熟练掌握完全平方公式的结构特征, 根据参数所在位置,结合公式,找出参数与已知项之间的数量关系,从而求出参数的值.计算过程中,要注意积的2倍的符号,避免漏解.
例23.把下列各式分解因式:
(1) (x2+y2)2-4x2y2 (2)4x2(x-1)-16(1-x)2 (3)16x4-72x2+81
解: (1) 原式=(x2+y2+2xy)(x2+y2-2xy)
=(x+y)2(x-y)2
(2)原式=4x2(x-1)-16(x-1)2
=4(x-1)[x2-4(x-1)]
=4(x-1)(x2-4x+4)
=4(x-1)(x-2)2
(3)原式=(4x2)2-2 · 4x2 · 9+92
= (4x2-9)2
=[(2x+3)(2x-3)]2
=(2x+3)2(2x-3)2
例24.已知,那么代数式的值是( )
A.2000 B.-2000 C.2001 D.-2001
【分析】解:∵,
∴,
∴
,
故选:B.
B
例25.已知三边长a,b,c满足,试判断的形状.
解:∵
=0,
∴,,,
∴,,,
∴为等腰三角形.
【8-1】多项式4ab2+16a2b2﹣12a3b2c的公因式是( )
A.4ab2c B.ab2 C.4ab2 D.4a3b2c
【8-2】下列分解因式错误的是( )
A. x2-y2= (x+y) (x-y) B. x2+6x+9= (x+3)2
C. x2+xy=x (x+y) D. x2+y2= (x+y)2
【8-3】若x2- 2(k+1)x+4是完全平方式,则k的值为( )
A.1或-3 B. -1或3 C.±1 D.±3
【8-4】若,则等于______.
C
D
A
2018
【8-5】已知a,b,c分别是△ABC三边的长,且a2+2b2+c2-2b(a+c)=0,请判断△ABC的形状,并说明理由.
解:△ABC是等边三角形.理由如下:
由a2+2b2+c2-2b(a+c)=0,
得a2-2ab+b2+b2-2bc+c2=0,
即(a-b)2+(b-c)2=0,
∴a-b=0,b-c=0,
∴a=b=c,
∴△ABC是等边三角形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
八上数学同步精品课件
人教版八年级上册
14.4整式的乘除与因式分解章节复习
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.梳理本章的知识,并会归纳总结;
2.熟练地运用法则进行整式的乘除运算;
3.熟练地运用平方差公式和完全平方公式;
4.会对一个多项式进行因式分解.
一、幂的乘法运算
同底数幂乘法法则:
am an=______.(m,n都是正整数) 即:同底数幂相乘,底数_____,指数_____.
条件:
结果:
am+n
不变
相加
①底数不变
①乘法
②同底数幂
②指数相加
拓展:当三个或三个以上同底数幂相乘时,
am·an·ap=______.(m,n,p都是正整数)
am+n+p
一、幂的乘法运算
幂的乘方法则:
(am)n=______.(m,n都是正整数) 即:幂的乘方,底数_____,指数_____.
amn
不变
相乘
拓展:[(am)n]p = amnp (m,n,p都是正整数)
n为偶数,
n为奇数.
幂的乘方法则的逆用:
amn = (am)n
= (an)m
一、幂的乘法运算
积的乘方法则:
(ab)n=______.(n为正整数) 即:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
anbn
拓展:(abc)n=anbncn.
积的乘方公式的逆用:
anbn=(ab)n
二、整式的乘法
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
【三步走】
(1)系数相乘;
(2)相同字母的幂相乘;
(3)其余字母连同它的指数不变,作为积的因式.
二、整式的乘法
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
注:积的项数与多项式的项数相同.
单项式与多项式相乘
单项式与单项式相乘
乘法分配律
转化
二、整式的乘法
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
三、整式的除法
同底数幂的除法法则:
am÷an=am-n(a≠0,m,n都是正整数,并且m>n)即 同底数幂相除,底数_____,指数_____.
不变
相减
规定:a0=1(a≠0) 这就是说,任何不等于0的数的0次幂都等于1.
三、整式的除法
单项式相除,把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
四、乘法公式
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,等于这两个数的平方差.
公式变形:
1.(a – b ) ( a + b) = a2 - b2
2.(b + a )( -b + a ) = a2 - b2
四、乘法公式
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
可以合写成 (a±b)2=a2±2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
注:公式中的字母a、b可以表示数、单项式和多项式.
(简记为:“首平方,尾平方,积的2倍中间放”)
四、乘法公式
1.添括号与去括号是互逆的,符号的变化是一致的. 添括号是否正确可用去括号检验.
2.不论怎样添括号,原式的值都不能改变,添括号法则在利用乘法公式的计算中应用较多.
五、因式分解
我们把一个多项式化成了几个整式的积的形式,像这样的式子变形叫做这个多项式的因式分解,也叫做把这个多项式分解因式.
因式分解与整式乘法是方向相反的变形,即
因式分解
整式乘法
五、因式分解
正确找出多项式的公因式的步骤:
1.定系数:公因式的系数是多项式各项系数的最大公约数.
2.定字母:字母取多项式各项中都有的相同的字母.
3.定指数:相同字母的指数取各项中最小的一个,即字母的最低次数.
多项式各项都含有的相同因式,叫做这个多项式各项的公因式.
如:pa+pb+pc的公因式是p.
五、因式分解
如果多项式的各项有公因式,可以把这个公因式提出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
五、因式分解
例1.计算:
(1)(a+b)2·(a+b)3 (2)(m-n)3·(m-n)2·(m-n)6 (3)(x-y)2·(y-x)5
解:(1)(a+b)2·(a+b)3 =(a+b)2+3 =(a+b)5
(2)(m-n)3·(m-n)2·(m-n)6 =(m-n)3+2+6 =(m-n)11
(3)(x-y)2·(y-x)5 =(y-x)2·(y-x)5 =(y-x)2+5 =(y-x)7
【点睛】公式am·an=am+n中的底数a不仅可以代表数、单项式,还可以代表多项式等其他代数式.当底数互为相反数的幂相乘时,先把底数统一,再进行计算.
n为偶数,
n为奇数.
同底数幂的乘法及其逆用
1
例2. (1)若xa=3,xb=4,xc=5,求2xa+b+c的值;
(2)已知23x+2=32,求x的值.
(2)∵ 23x+2=32=25,
∴3x+2=5,
∴x=1.
解:(1) 2xa+b+c=2xa·xb·xc=120;
【点睛】(1)关键是逆用同底数幂的乘法公式,将所求代数式转化为几个已知因式的乘积的形式,然后再求值.
(2)关键是将等式两边转化为底数相同的形式,然后根据指数相等列方程解答.
【1-1】计算:(1) x4·x6=____;(2) a·a4=_____;
(3)5×54×53=______;(4) x2n+1·x3n-1=______.
【1-2】若am=3,an=5,则am+n等于( )
A.243 B.125 C.8 D.15
x10
a5
58
x5n
D
【1-3】计算下列各题:
(4)-a3·(-a)2·(-a)3.
(2)(a-b)3·(b-a)4;
(3) (-3)×(-3)2 ×(-3)3;
(1)(2a+b)2n+1·(2a+b)3;
解:(1)(2a+b)2n+1·(2a+b)3=(2a+b)2n+4;
(2)(a-b)3·(b-a)4=(a-b)7;
(3) (-3)×(-3)2 ×(-3)3=36;
(4)-a3·(-a)2·(-a)3=a8.
幂的乘方及其逆用
2
例3.计算:
(1) (x4)3·x6;
(2) a2(-a)2(-a2)3+a10.
解: (1) (x4)3·x6 =x12·x6= x18;
(2) a2(-a)2(-a2)3+a10
= -a2·a2·a6+a10
= -a10+a10
= 0
【点睛】与幂的乘方有关的混合运算中,一般先算幂的乘方,再算同底数幂的乘法,最后算加减,然后合并同类项.
例4.已知10m=3,10n=2,求下列各式的值.
(1)103m; (2)102n; (3)103m+2n.
解:(1)103m=(10m)3=33=27;
(2)102n=(10n)2=22=4;
(3)103m+2n=103m×102n=(10m)3× (10n)2 =27×4=108.
【点睛】此类题的关键是逆用幂的乘方及同底数幂的乘法公式,将所求代数式正确变形,然后代入已知条件求值即可.
例5.比较3500,4400,5300的大小.
分析:这三个幂的底数不同,指数也不相同,不能直接比较大小,通过观察,发现指数都是100的倍数,故可以考虑逆用幂的乘方法则.
解:3500=(35)100=243100,4400=(44)100=256100,5300=(53)100=125100.
∵256>243>125,
∴4400>3500>5300.
【点睛】比较底数大于1的幂的大小的方法有两种:(1)底数相同,指数越大,幂就越大;(2)指数相同,底数越大,幂就越大.故在此类题中,一般先观察题目所给数据的特点,将其转化为同底数的幂或同指数的幂,然后再进行大小比较.
【2-1】下列计算正确的是( )
A.a3·a2=a6 B.(a3)2=a5 C.(a2)3=a6 D.a2+a3=a5
【2-2】若,则等于( )
A. B. C. D.
【2-3】已知,,,,则 a、b、c的大小关系是( )
A.b>c>a B.a>b>c C.c>a>b D.a
D
A
【2-4】计算:
(1); (2); (3); (4).
解:(1)
(2)
(3)
(4)
积的乘方及其逆用
3
例6.计算:
(1)(-4ab)3; (2)(-3ab2c3)3; (3)(-xmy3n)2.
解:
(1)(-4ab)3=(-4)3·a3·b3=-64a3b3
(2)(-3ab2c3)3=(-3)3·a3·(b2)3·(c3)3=-27a3b6c9
(3)(-xmy3n)2=(-1)2·(xm)2·(y3n)2=x2my6n
例7.计算:(1)0.22022×52022; (2)
解:(1)0.22022×52022
=(0.2×5)2022
=12022
=1
解:(2)
【点睛】逆用积的乘方公式an·bn=(ab)n,要灵活运用,对于不符合公式的形式,要通过恒等变形,转化为公式的形式,再运用此公式可进行简便运算.
【3-1】若(2ambm+n)3=8a9b15成立,则( )
m=3,n=2 B. m=n=3 C.m=6,n=2 D.m=3,n=5
【3-2】现规定一种新的运算“※”:a※b=ba,如3※2=23=8,则2※(-5)
=______,3※(-2x3y4)=__________.
A
25
-8x9y12
【3-3】计算:
(1)(2)
(1)解原式
(2)解原式
整式的乘法
4
例8.计算:
(2x)3(-5xy2); (2) 3x2y2 (-2xy2z)2 ; (3) (x3y)(-3xy2)3(x)2.
解:(1) (2x)3(-5xy2) =8x3(-5xy2)= [8×(-5)](x3·x)·y2=-40x4y2
(2)
(3)
例9.若与的积与是同类项,求m、n.
解:∵ ,
又∵与的积与是同类项,
∴
解得:m=2,n=3.
【点睛】单项式乘单项式就是把它们的系数和同底数幂分别相乘,结合同类项的定义,列出二元一次方程组求出参数的值,然后代入求值即可.
例10.计算:
(1); (2) [xy(x2﹣xy)﹣x2y(x﹣y)] 3xy2
解:
.
解:[xy(x2﹣xy)﹣x2y(x﹣y)] 3xy2
=(x3y﹣x2y2﹣x3y+x2y2) 3xy2
=0.
例11.先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b),其中a=-1,b=1.
当a=-1,b=1时,
解:原式=a3-8b3-(a2-5ab)(a+3b)
=a3-8b3-a3-3a2b+5a2b+15ab2
=-8b3+2a2b+15ab2.
原式=-8+2-15=-21.
例12.已知ax2+bx+1(a≠0)与3x-2的积不含x2项,也不含x项,求系数a、b的值.
解:(ax2+bx+1)(3x-2)
=3ax3+(-2a+3b)x2+(-2b+3)x-2.
∵积不含x2项,也不含x项,
【点睛】解决此类问题首先要利用多项式乘法法则计算出展开式,合并同类项后,再根据不含某一项,可得这一项系数等于零,再列出方程(组)解答.
【4-1】计算2x(3x2+1),正确的结果是( )
A.5x3+2x B.6x3+1 C.6x3+2x D.6x2+2x
【4-2】在一次数学课.上,学习了单项式乘多项式.小明回家后拿出课堂笔记本复习,发现这样一道题: -3x(-2x2+3x-1)=6x3+□+3x,“□”的地方被墨水污染了,你认为“□”内应填写( )
A.9x2 B.-9x2 C.9x D.-9x
【4-3】要使6x3(x2+ax+1)的展开式中不含x4项,则a应等于( )
A.-6 B. -1 C. D.0
C
B
D
【4-4】计算:
(2x+3y) (x -2y) (2) (-2a+3) (5+a) (3) (-3m+2)2
(4) (m+2) (2m2-m-3)
解: (1) 原式= 2x2-4xy+3xy-6y2=2x2-xy -6y2
(2)原式=-10a-2a2+15+3a=-2a2-7a+15
(3)原式= (-3m+2) (-3m+2)= 9m2-6m-6m+4= 9m2-12m+4
(4)原式= 2m3-m2-3m+4m2-2m-6= 2m3-m2+4m2-3m-2m-6= 2m3+3m2-5m-6
同底数幂的除法及其逆用
5
例13.计算:
(1)(-xy)13÷(-xy)8;(2)(x-2y)3÷(2y-x)2;(3)(a2+1)6÷(a2+1)4÷(a2+1)2.
(3)原式=(a2+1)6-4-2=(a2+1)0=1.
解:(1)原式=(-xy)13-8=(-xy)5=-x5y5;
(2)原式=(x-2y)3÷(x-2y)2=x-2y;
例14. 已知am=12,an=2,a=3,求am-n-1的值.
【点睛】解此题的关键是逆用同底数幂的除法即am-n =am÷an,对am-n-1进行变形,再代入数值进行计算.
解:∵am=12,an=2,a=3,
∴am-n-1=am÷an÷a=12÷2÷3=2.
【5-1】a12 ÷ a5=_____,(ab)3 ÷ (ab)2=_____.
(a+b)6÷(a+b)2=______,(a-c)8÷ (c-a)2=______.
【5-2】若2m=15,2n=5,则2m-n的值是_____.
a7
ab
(a-c)6
3
【5-3】计算:
(1) x7÷x5 (2) m8÷m8 (3) (-a)10÷(-a)7 (4) (xy)5÷(xy)3
解:(1) x7÷x5=x7-5=x2
(2) m8÷m8=m8-8=m0=1
(3) (-a)10÷(-a)7=(-a)10-7=(-a)3=-a3
(4) (xy)5÷(xy)3=(xy)5-3=(xy)2=x2y2
(a+b)4
整式的除法
6
例15.计算:
(12a3-6a2+3a)÷3a ; (2) (6x3y4z-4x2y3z+2xy3)÷2xy3.
解:(1)原式=12a3÷3a-6a2÷3a+3a÷3a
=4a2-2a+1;
(2)原式=6x3y4z÷2xy3-4x2y3z÷2xy3+2xy3÷2xy3
=3x2yz-2xz+1.
例16.先化简,后求值:[2x(x2y-xy2)+xy(xy-x2)]÷x2y,其中x=2022,y=2021.
解:原式=(2x3y-2x2y2+x2y2-x3y)÷x2y
原式=x-y=2022-2021=1.
=x-y.
把x=2022,y=2021代入上式,得
【6-1】(16x3-8x2+____ ) ÷ (-2x)=-8x2+4x-2
【6-2】若某长方形的面积为4a2-6ab+2a,它的长为2a,则它的宽是_________.
4x
2a-3b+1
解:(1)原式=6ab÷a+5a÷a=6b+5;
(2)原式=15x2y÷5xy-10xy2÷5xy=3x-2y;
(3)原式=72x3y4÷(-9xy2)+(-36x2y3)÷(-9xy2)+9xy2÷(-9xy2)
=-8x2y2+4xy-1.
【6-3】计算:
(6ab+5a)÷a ; (2)(15x2y-10xy2)÷5xy; (3)(72x3y4-36x2y3+9xy2)÷(-9xy2).
乘法公式的运用
7
例17.计算:
(1)(2) .
(1)解:原式=
;
(2)解:原式=
=
例18.运用乘法公式计算:
(1) (x+2y-3)(x-2y+3) (2) (a+b+c)2
解:(1) (x+2y-3)(x-2y+3)
=[(x+(2y-3)][(x-(2y-3)]
=x2-(2y-3)2
=x2-(4y2-12y+9)
=x2-4y2+12y-9
(2) (a+b+c)2
=[(a+b)+c]2
=(a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc
【点睛】第1小题选用平方差公式进行计算,需要分组.分组方法是“符号相同的为一组,符号相反的为另一组”.第2小题要把其中两项看成一个整体,再按照完全平方公式进行计算.
例19.化简求值:已知,求代数式的值.
解:∵,
∴,
原式=
,
∵,
∴原式.
例20.(1)已知,,求①的值;②的值;
(2)已知,求的值.
解:(1)①,,
,
.
②,
.
例20.(1)已知,,求①的值;②的值;
(2)已知,求的值.
解:(2),且,
,
,
,
.
【7-1】下列计算正确的是( )
A. B.
C. D.
【7-2】计算:( )
A.﹣2000 B.﹣1995 C.2000 D.1995
【7-3】(2+1)(22+1)(24+1)…(216+1)的结果为( )
A.232-1 B.232+1 C.232 D.216
B
B
A
【7-4】计算:
(1) (2)2(x﹣1)2 ﹣x(x﹣2)+(3x﹣2)(3x+2).
(1)解原式=
=
=;
(2)解原式=
=10x2﹣2x﹣2.
【7-5】运用乘法公式计算:
(1) (x-3y+1)2 (2) (3a+b-c) (3a-b+c) (3) 29×31×(302+1)
(3)原式=(30-1) × (30+1) × (302+1)
= (302-1) × (302+1)
= (302)2-12
=9002-1
=810000-1
=809999
【7-6】先化简,再求值:,其中,b=2.
解原式
,
将,b=2代入,
原式.
因式分解及应用
8
例21.下列由左边到右边的变形,属于因式分解的是( )
A. B.
C. D.
【分析】解:A.由左边到右边的变形属于因式分解,故本选项符合题意;
B.,原式等式两边不相等,即从等式的左边到右边的变形不属于因式分解,故本选项不符合题意;
C.从等式的左边到右边的变形不属于因式分解,故本选项不符合题意;
D.从等式的左边到右边的变形属于整式乘法,不属于因式分解,故本选项不符合题意;
故选:A.
A
【点睛】因式分解与整式乘法是相反方向的变形,即互逆运算,二者是一个式子的不同表现形式.因式分解的右边是两个或几个因式积的形式,整式乘法的右边是多项式的形式.
例22.已知是完全平方式,则m的值为( )
A.8 B. C.24 D.
【分析】解:∵是一个完全平方式,
∴mx=±2 2x 6,
解得:m=±24,
故选:D.
D
【点睛】本题要熟练掌握完全平方公式的结构特征, 根据参数所在位置,结合公式,找出参数与已知项之间的数量关系,从而求出参数的值.计算过程中,要注意积的2倍的符号,避免漏解.
例23.把下列各式分解因式:
(1) (x2+y2)2-4x2y2 (2)4x2(x-1)-16(1-x)2 (3)16x4-72x2+81
解: (1) 原式=(x2+y2+2xy)(x2+y2-2xy)
=(x+y)2(x-y)2
(2)原式=4x2(x-1)-16(x-1)2
=4(x-1)[x2-4(x-1)]
=4(x-1)(x2-4x+4)
=4(x-1)(x-2)2
(3)原式=(4x2)2-2 · 4x2 · 9+92
= (4x2-9)2
=[(2x+3)(2x-3)]2
=(2x+3)2(2x-3)2
例24.已知,那么代数式的值是( )
A.2000 B.-2000 C.2001 D.-2001
【分析】解:∵,
∴,
∴
,
故选:B.
B
例25.已知三边长a,b,c满足,试判断的形状.
解:∵
=0,
∴,,,
∴,,,
∴为等腰三角形.
【8-1】多项式4ab2+16a2b2﹣12a3b2c的公因式是( )
A.4ab2c B.ab2 C.4ab2 D.4a3b2c
【8-2】下列分解因式错误的是( )
A. x2-y2= (x+y) (x-y) B. x2+6x+9= (x+3)2
C. x2+xy=x (x+y) D. x2+y2= (x+y)2
【8-3】若x2- 2(k+1)x+4是完全平方式,则k的值为( )
A.1或-3 B. -1或3 C.±1 D.±3
【8-4】若,则等于______.
C
D
A
2018
【8-5】已知a,b,c分别是△ABC三边的长,且a2+2b2+c2-2b(a+c)=0,请判断△ABC的形状,并说明理由.
解:△ABC是等边三角形.理由如下:
由a2+2b2+c2-2b(a+c)=0,
得a2-2ab+b2+b2-2bc+c2=0,
即(a-b)2+(b-c)2=0,
∴a-b=0,b-c=0,
∴a=b=c,
∴△ABC是等边三角形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
