分式[下学期]
图片预览







文档简介
课件22张PPT。中考第一轮复习(5)分式考点1.整式的除法(1)同底数幂的除法
同底数幂相除,底数不变,指数相减.
am÷an=am-n(a≠0,m,n为正整数,m>n).(2)单项式除以单项式
单项式除以单项式,把系数,同底数
幂分别相除后,作为商的因式,对于
只在被作式里含有的字母,则连同
它的指数作为商的一个因式.(3)多项式除以单项式
多项式除以单项式,先用这
个多项式的每一项除以这个单
项式,再把所得的商相加.考点2.分式
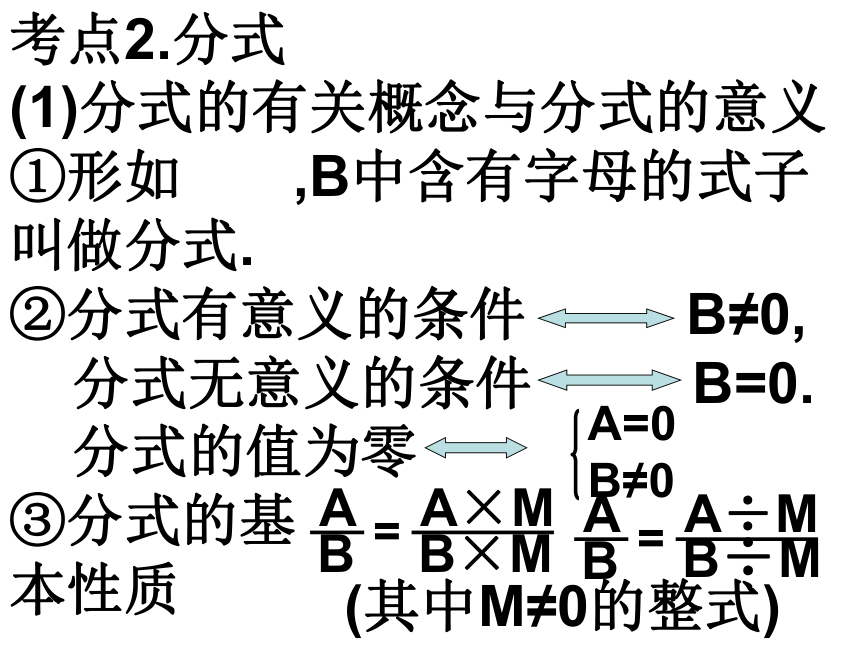
(1)分式的有关概念与分式的意义
①形如 ,B中含有字母的式子
叫做分式.
②分式有意义的条件 B≠0,
分式无意义的条件 B=0.
分式的值为零
③分式的基
本性质A=0
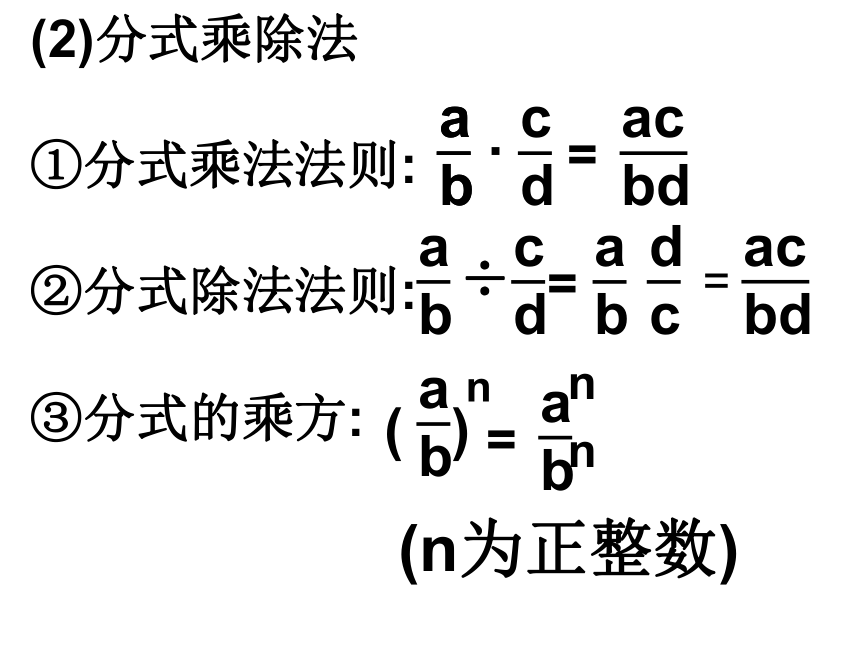
B≠0(其中M≠0的整式)(2)分式乘除法
①分式乘法法则:
②分式除法法则:
③分式的乘方:÷=acbd=( )n=nn(n为正整数)(3)分式的加减法
①约分:把一个分式的分子分母中公因
式约去(即分子分母同时除以它们的公
因式)叫做分式的约分.分子分母中没
有公因式时叫做最简分式.
②分式的通分把几个异分母的分式化
为与原来的分式相等的同分母的分式
叫做分式的通分
③同分母分式相加减的法则
④异分母分式相加减的法则. (4)可化为一元一次方程的分式方程
①分式方程:分母中含有未知数的方程叫
做分式方程.
②解分式方程的一般步骤:
a.在方程两边都乘以最简公分母,约去分
母,化为整式方程.
b.解这个整式方程
c.把整式方程的根代入最简公分母,看结
果是不是零,使最简公分母为零的根是原
方程的增根,必须舍去.
③分式方程的应用.考点3.零指数幂与负指数幂
(1)零指数幂:a0=1 (a≠ 0)
am÷am=am-m=1 (a≠ 0)
(2)负整数指数幂a-n=
(a≠ 0,n为正整数)
(3)科学记数法表示绝对值较大数和绝对
值较小的数.写成形如:a×10n (其中1≤|a|<10,n为整数)重难专攻.综合方法专攻1.化简并求值例1.先化简再求值(其中m=--------)1√3-2专攻2.解分式方程的化归思想(1)可化为一元一次方程的分式方程的
解法:
A.去分母法:①去分母,②去括号
③移项④合并同类项⑤检验所求出的
方程的根是否是增根 ,
B.换元法
(2)分式方程的应用问题:①设未知数,
②列出相关代数式,③列方程,④解方程检
验,⑤作答.中考能力提升题例1.整式的除法1.下列计算正确的是( )A.b2·b3=b6 B.(-a2)3=a6
C.(ab)2=ab2 D.(-a)6÷(-a)3=-a3
2.计算:(a2b)2÷a4=____题例2.分式3.当x___时,分式 有意义.
4.某林场原计划在一定期限内固
沙造林240公顷,实际每天固沙造
林的面积比原计划多4公顷,结果
提前5天完成任务,设原计划每天
固沙造林x公顷,根据题意可列方
程为________.题例3.分式的加减乘除运算 5.若分式 的值为零,则x的
值为( )
A.3 B.3或-3 C.-3 D.0
6.化简( ) 的结果
是_____.xx-2-xx+2÷4x2-x剑指中考重击1.条件开放题1.先化简代数式,
然后请你自选一组a,b的值代入求值.重击2.归纳猜想题(1)观察下列各式:112=13×4=-,,,…,由此可推测:(2)请猜想出能表示出(1)的特点的一般
规律,用含字母n的等式表示出来(n为
正整数),并证明.(3)请用(2)中的规律计算:
,重击3.阅读理解题解方程13x-4-10x-3=4x-5-1x-1先阅读解题过程,再回答问题.原方程变形为3x+1(x-4)(x-3)=3x+1(x-5)(x-1)两边同除以(3x+1),得1(x-4)(x-3)=1(x-5)(x-1)(第一步)(第二步)所以(x-4)(x-3)=(x-5)(x-1),(第三步)即 x2-7x+12=x2-6x+5,(第四步)解得x=7,(第五步)经检验x=7是原方程的解(1)第一步的方法是:____
(2)本题解题有错否?没,说出依据,有纠正大显身手1.若x<2.则 的值为( )x-2|x-2|A.-1 B.0 C.1 D.22.若关于x的方程 有增根,
则m的值为( )=0A.3 B.2 C.1 D.-13.若分式 的值为零,则x的值
为( )x2-9x2-4x+3A.3 B.3或-3 C.-3 D.04.已知两个分式A= ,B=4x2-41x+2+12-x下面有三个结论(1)A=B(2)A,B互为相
反数(3)A,B互为倒数.请问哪个正确?5.有这样一道题:计算x2-2x+1x2-1÷x-1x2+x-x的值,其中x=2004,甲同学把x=2004
错抄成x=2040,但他的计算结果也是
正确的,你说这是怎么回事?6.已知P=Q=(x+y)2 -2y(x+y)小敏,小聪两人在x=2,y=-1的条件下
分别计算了P和Q的值,小敏说P的值
比Q大,小聪说Q的值比P大,请你判断
谁的结论正确,并说明理由.
同底数幂相除,底数不变,指数相减.
am÷an=am-n(a≠0,m,n为正整数,m>n).(2)单项式除以单项式
单项式除以单项式,把系数,同底数
幂分别相除后,作为商的因式,对于
只在被作式里含有的字母,则连同
它的指数作为商的一个因式.(3)多项式除以单项式
多项式除以单项式,先用这
个多项式的每一项除以这个单
项式,再把所得的商相加.考点2.分式
(1)分式的有关概念与分式的意义
①形如 ,B中含有字母的式子
叫做分式.
②分式有意义的条件 B≠0,
分式无意义的条件 B=0.
分式的值为零
③分式的基
本性质A=0
B≠0(其中M≠0的整式)(2)分式乘除法
①分式乘法法则:
②分式除法法则:
③分式的乘方:÷=acbd=( )n=nn(n为正整数)(3)分式的加减法
①约分:把一个分式的分子分母中公因
式约去(即分子分母同时除以它们的公
因式)叫做分式的约分.分子分母中没
有公因式时叫做最简分式.
②分式的通分把几个异分母的分式化
为与原来的分式相等的同分母的分式
叫做分式的通分
③同分母分式相加减的法则
④异分母分式相加减的法则. (4)可化为一元一次方程的分式方程
①分式方程:分母中含有未知数的方程叫
做分式方程.
②解分式方程的一般步骤:
a.在方程两边都乘以最简公分母,约去分
母,化为整式方程.
b.解这个整式方程
c.把整式方程的根代入最简公分母,看结
果是不是零,使最简公分母为零的根是原
方程的增根,必须舍去.
③分式方程的应用.考点3.零指数幂与负指数幂
(1)零指数幂:a0=1 (a≠ 0)
am÷am=am-m=1 (a≠ 0)
(2)负整数指数幂a-n=
(a≠ 0,n为正整数)
(3)科学记数法表示绝对值较大数和绝对
值较小的数.写成形如:a×10n (其中1≤|a|<10,n为整数)重难专攻.综合方法专攻1.化简并求值例1.先化简再求值(其中m=--------)1√3-2专攻2.解分式方程的化归思想(1)可化为一元一次方程的分式方程的
解法:
A.去分母法:①去分母,②去括号
③移项④合并同类项⑤检验所求出的
方程的根是否是增根 ,
B.换元法
(2)分式方程的应用问题:①设未知数,
②列出相关代数式,③列方程,④解方程检
验,⑤作答.中考能力提升题例1.整式的除法1.下列计算正确的是( )A.b2·b3=b6 B.(-a2)3=a6
C.(ab)2=ab2 D.(-a)6÷(-a)3=-a3
2.计算:(a2b)2÷a4=____题例2.分式3.当x___时,分式 有意义.
4.某林场原计划在一定期限内固
沙造林240公顷,实际每天固沙造
林的面积比原计划多4公顷,结果
提前5天完成任务,设原计划每天
固沙造林x公顷,根据题意可列方
程为________.题例3.分式的加减乘除运算 5.若分式 的值为零,则x的
值为( )
A.3 B.3或-3 C.-3 D.0
6.化简( ) 的结果
是_____.xx-2-xx+2÷4x2-x剑指中考重击1.条件开放题1.先化简代数式,
然后请你自选一组a,b的值代入求值.重击2.归纳猜想题(1)观察下列各式:112=13×4=-,,,…,由此可推测:(2)请猜想出能表示出(1)的特点的一般
规律,用含字母n的等式表示出来(n为
正整数),并证明.(3)请用(2)中的规律计算:
,重击3.阅读理解题解方程13x-4-10x-3=4x-5-1x-1先阅读解题过程,再回答问题.原方程变形为3x+1(x-4)(x-3)=3x+1(x-5)(x-1)两边同除以(3x+1),得1(x-4)(x-3)=1(x-5)(x-1)(第一步)(第二步)所以(x-4)(x-3)=(x-5)(x-1),(第三步)即 x2-7x+12=x2-6x+5,(第四步)解得x=7,(第五步)经检验x=7是原方程的解(1)第一步的方法是:____
(2)本题解题有错否?没,说出依据,有纠正大显身手1.若x<2.则 的值为( )x-2|x-2|A.-1 B.0 C.1 D.22.若关于x的方程 有增根,
则m的值为( )=0A.3 B.2 C.1 D.-13.若分式 的值为零,则x的值
为( )x2-9x2-4x+3A.3 B.3或-3 C.-3 D.04.已知两个分式A= ,B=4x2-41x+2+12-x下面有三个结论(1)A=B(2)A,B互为相
反数(3)A,B互为倒数.请问哪个正确?5.有这样一道题:计算x2-2x+1x2-1÷x-1x2+x-x的值,其中x=2004,甲同学把x=2004
错抄成x=2040,但他的计算结果也是
正确的,你说这是怎么回事?6.已知P=Q=(x+y)2 -2y(x+y)小敏,小聪两人在x=2,y=-1的条件下
分别计算了P和Q的值,小敏说P的值
比Q大,小聪说Q的值比P大,请你判断
谁的结论正确,并说明理由.
