第25章 概率初步(章末小结) 优质课件(50张PPT)
文档属性
| 名称 | 第25章 概率初步(章末小结) 优质课件(50张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 09:01:14 | ||
图片预览









文档简介
(共50张PPT)
九上数学同步优质课件
人教版九年级上册
概率初步章末小结
第二十五章 概率初步
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.梳理本章的知识要点,回顾与复习本章知识;
2.巩固并能熟练运用列举法、列表法和树状图法求概率;(重、难点)
3.能应用频率估计概率解决生活中的实际问题.
必然事件:在一定条件下,有些事件必然会发生,这样的事件称为必然事件.
不可能事件:在一定条件下,有些事件必然不会发生,这样的事件称为不可能事件.
确定性事件:必然事件与不可能事件统称确定性事件.
随机事件:在一定条件下,有些事件有可能发生,也有可能不发生,事先无法确定,这种事件称为随机事件.
一、事件的分类及其概念
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率P(A)= .
事件发生的可能性越大,它的概率越接近1;反之,事件发生的可能性越小,它的概率越接近0(如下图).
二、概率的概念
三、随机事件的概率的求法
1.直接列举法求随机事件的概率:
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,那么出现每一种结果的概率都是 .
如果事件A包括其中的m种可能的结果,那么事件A发生的概率
P(A)=
【适用范围】直接列举法比较适合用于最多涉及两个试验因素或分两步进行的试验,且事件总结果的种数比较少的等可能性事件.
三、随机事件的概率的求法
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
列表法中表格构造特点:
2.列表法求随机事件的概率:
三、随机事件的概率的求法
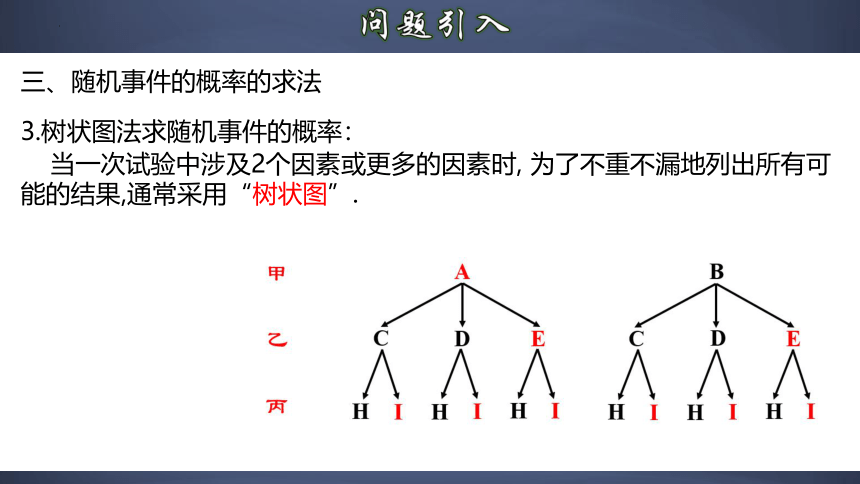
3.树状图法求随机事件的概率:
当一次试验中涉及2个因素或更多的因素时, 为了不重不漏地列出所有可能的结果,通常采用“树状图”.
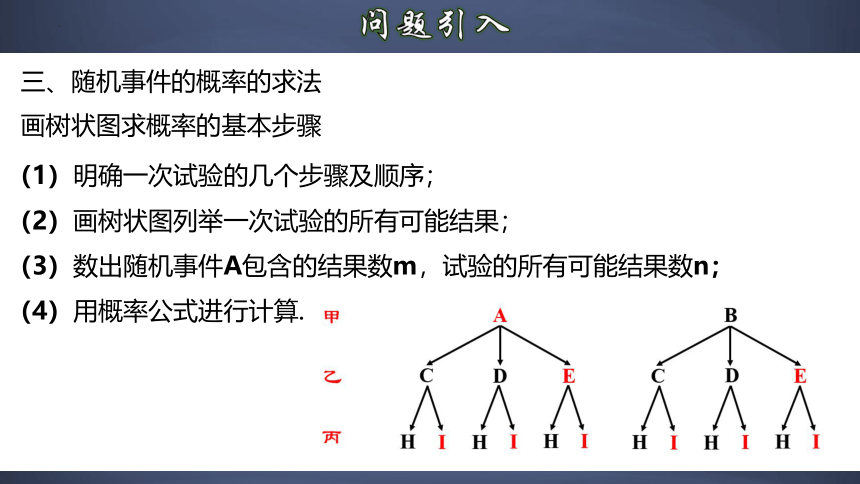
画树状图求概率的基本步骤
(1)明确一次试验的几个步骤及顺序;
(2)画树状图列举一次试验的所有可能结果;
(3)数出随机事件A包含的结果数m,试验的所有可能结果数n;
(4)用概率公式进行计算.
三、随机事件的概率的求法
四、频率来估计概率
4.树状图法求随机事件的概率:
①当实验的所有结果不是有限个,或各种可能结果发生的可能性不相等时,我们用大量重复试验中随机事件发生的稳定频率来估计概率.
②频率与概率的关系:两者都能定量地反映随机事件可能性的大小,但频率具有随机性,概率是自身固有的性质,不具有随机性.
事件的分类
1
例1.投掷两枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,则下列事件为随机事件的是( )
A.两枚骰子向上一面的点数之和大于1
B.两枚骰子向上一面的点数之和等于1
C.两枚骰子向上一面的点数之和大于12
D.两枚骰子向上一面的点数之和等于12
D
事件的分类
1
例2.下列说法中正确的是( )
A.“任意画出一个等边三角形,它是轴对称图形”是随机事件
B.“任意画出一个平行四边形,它是中心对称图形”是必然事件
C.“概率为0.0001的事件”是不可能事件
D.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
B
【1-1】下列事件中,属于随机事件的是( )
A.买一张体育彩票中奖
B.太阳从西边落下
C.掷一枚质地均匀的正六面体骰子所得点数不超过6
D.口袋中装有10个红球,从中摸出一个白球
【1-2】下列成语所描述的事件是不可能事件的是( )
A.百步穿杨 B.瓮中捉鳖 C.水中捞月 D.守株待兔
【1-3】“一个不透明的袋子中装有3个小球,它们的标号分别为1,2,3,从中摸出1个小球,标号为“4”,这个事件是____________(填“必然事件”“不可能事件”或“随机事件”).
A
C
不可能事件
判断事件发生的可能性大小
2
例3.如图,转盘中个扇形的面积都相等,任意转动转盘次,当转盘停止转动时,估计下列个事件发生的可能性大小,其中事件发生的可能性最大的是( )
A.指针落在标有的区域内
B.指针落在标有的区域内
C.指针落在标有偶数或奇数的区域内
D.指针落在标有奇数的区域内
C
【2-1】质地均匀的骰子六个面分别刻有1到6的点数,掷两次骰子,得到向上一面的两个点数.则下列事件中,发生可能性最大的是( )
A.点数都是偶数 B.点数的和是奇数
C.点数的和小于12 D.点数的和大于10
C
【2-1】如图,转盘中5个扇形的面积都相等,任意转动转盘一次,当转盘停止转动时,把下列事件的序号按发生的可能性从小到大的顺序排列为______________.
①指针落在标有3的区域内;
②指针落在标有奇数的区域;
③指针落在标有6的区域内;
④指针落在标有偶数或奇数的区域.
③<①<②<④
【2-3】为了了解学生每月的零用钱情况,从甲、乙、丙三个学校各随机抽取200名学生,调查了他们的零用钱情况(单位:元)具体情况如下:
在调查过程中,从______(填“甲”,“乙”或“丙”)校随机抽取学生,抽到的学生“零用钱不低于300元”的可能性最大.
学校频数零 用钱 100≤x<200 200≤x<300 300≤x<400 400≤x<500 500以上 合计
甲 5 35 150 8 2 200
乙 16 54 68 52 10 200
丙 0 10 40 70 80 200
丙
用直接列举法求概率
3
例4.桌子上有三个不透明的盒子,小慧将一个白球放入其中一个大盒子,大鹏将一个黑球也随机放入一个盒子,则两个球不在同一个盒子里的概率为( )
A. B. C. D.
【分析】解:假设三个不透明的盒子分别为A,B,C,
当小慧把白球放入盒子A中,大鹏则可能把黑球放入A,B,C中;
当小慧把白球放入盒子B中,大鹏则可能把黑球放入A,B,C中;
当小慧把白球放入盒子C中,大鹏则可能把黑球放入A,B,C中;
根据概率定义可得所有等可能出现的结果数为9,其中两个球在同一盒子的事件数为3,分别为AA,BB,CC;
所以,两个球不在同一盒子的结果数为9-3=6,
所以,两个球不在同一个盒子里的概率为.
D
【3-1】若从长度分别为3、5、6、9的四条线段中任取三条,则能组成三角形的概率为( )
A. B. C. D.
A
【3-2】如图,随机闭合开关K1,K2,K3中的两个,则能让两盏灯泡同时发光的概率为( )
A. B. C. D.
B
用列表法求概率
4
例5.现有《北京冬奥会―雪上运动》纪念邮票4张.纪念邮票封面设计,分别是A越野滑雪;B高山滑雪;C冬季两项;D自由式滑雪(四张卡片除字母和图案内容外,其余完全相同).姐弟两人做游戏,他们将这四张卡片混在一起,背面朝上放好.若两人分别随机抽取一张卡片(不放回),请求出恰好姐姐抽到A越野滑雪,弟弟抽到B高山滑雪的概率.
A B C D
A / (A,B) (A,C) (A,D)
B (B,A) / (B,C) (B,D)
C (C,A) (C,B) / (C,D)
D (D,A) (D,B) (D,C) /
解:用列表法:
由表格可知:共有12种结果,并且它们的可能性相同,其中姐姐抽到A越野滑雪,弟弟抽到B高山滑雪的结果数为1.
(A越野滑雪B高山滑雪)=.
用列表法求概率
4
例6.今年猪肉价格受非洲猪瘟疫情影响,有较大幅度的上升,为了解某地区养殖户受非洲猪瘟疫情感染受灾情况,现从该地区建档的养殖户中随机抽取了部分养殖户进行了调查(把调查结果分为四个等级:A级:非常严重;B级:严重;C级:一般;D级:没有感染),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
(1)本次抽样调查的养殖户的总户数是______户;
把图2条形统计图补充完整.
(2)若该地区建档的养殖户有1500户,求非常严
重与严重的养殖户一共有多少户?
(3)某调研单位想从3户建档养殖户(分别记为a,
b,c)中随机选取两户,进一步跟踪监测病毒传
播情况,请用列表的方法求出选中养殖户c的概
率.
(1)解:总的户数:21÷35%=60(户),
“C级”的户数:60﹣9﹣21﹣9=21(户),
补全条形统计图如图所示:
(2)解:1500×=750(户),
答:若该地区建档的养殖户有1500户中“严重”和“非常严重”的养殖户一共有750户;
(3)解:用表格表示所有可能出现的情况如右图:
共有6种不同的情况,其中选中c的情况有4种,
∴即概率为:.
【4-1】小丽的爸爸积极参加社区防疫志愿服务,根据社区安排,志愿者将被随机分配到以下小组中的一个:A组(体温检测)、B组(环境消杀)、C组(便民代购)、D组(宣传巡查)开展服务工作.
(1)小丽的爸爸被分配到C组的概率是 ;
(2)若小丽的班主任刘老师也加入了该社区的志愿者队伍,那么刘老师和小丽的爸爸被分到同一组的概率是多少?请用列表的方法写出分析过程.
(2)解:列表如下:
小组 A B C D
A
B
C
D
因为一共有16种等可能的结果,其中刘老师和小丽的爸爸被分到同一组的有4种结果,所以P(两人被分到同一组).
答:刘老师和小丽的爸爸被分到同一组的概率是.
【4-2】在不透明的袋中有大小、形状和质地完全相同的小球,它们分别标有数字-1、-2、1、2,从袋中任意摸出一个小球(不放回),将袋中的小球搅匀后,再从袋中摸出另一个小球.
(1)请你表示摸出小球上的数字出现的所有结果;
解:(1)可能出现的所有结果如下:
∴共12种结果.
(2)若规定:如果摸出的两个小球上的数字都是方程x2-3x+2=0的根,则小明赢;如果摸出两个小球上的数字都不是x2-3x+2=0的根,则小亮赢.你认为这个游戏规则对小明、小亮公平吗 请说明理由.
解:(2)由方程x2-3x+2=0,解得,x1=1,x2=2
∴P(小明赢)= = ,P(小亮赢)= =
∴游戏公平.
【4-3】为了继续宣传新冠疫苗接种的重要性,某小区物业部门准备在已经接种疫苗的居民中招募2名志愿宣传者,现有2名男性2名女性共4名居民报名.请用列表的方法,求要从这4人中随机挑选2人,恰好抽到一名男性和一名女性的概率.
解:由题可列下表:
由表可知,共有12种等可能的结果,而两个人选中一名男性和一名女性的结果有8种,
∴.
用画树形图法求概率
5
例7.甲口袋中装有2个相同小球,它们分别写有数字1,2;乙口袋中装有3个相同小球,它们分别写有数字3,4,5;丙口袋中装有2个相同小球,它们分别写有数字6,7.从三个口袋各随机取出1个小球.用画树状图求:
(1)取出的3个小球上恰好有一个偶数的概率;
(2)取出的3个小球上全是奇数的概率.
解:画树状图为:
共有12种等可能的结果,其中取出的3个小球,上恰好有一个偶数的结果数为5,所以取出的3个小球5上恰好有一个偶数的概率=
(2)取出的3个小球上全是奇数的结果数为2,所2.以取出的3个小球.上全是奇数的概率==
用画树形图法求概率
5
例8.某校开展主题为“防疫常识知多少”的调查活动,抽取了部分学生进行调查,调查问卷设置了:非常了解、:比较了解、:基本了解、:不太了解四个等级,要求每个学生填且只能填其中的一个等级,采取随机抽样的方式,并根据调查结果绘制成如图所示不完整的频数分布表和统计图,根据以上信息回答下列问题:
等级 频数 频率
20 0.4
15
10 0.2
0.1
(1)频数分布表中_____,_____,将统计图补充完整;
解:(1)被调查的总人数为:
(人),
(人),
,
(2)若该校有学生1000人,请根据抽样调查结果估算该校“非常了解”和“比较了解”防疫常识的学生共有多少人?
解:(2)根据频数分布表知,“非常了解”和“比较了解”的频率之和为:,
利用样本估计总体的思想,若该校有学生1000人,校“非常了解”和“比较了解”防疫常识的学生共有:(人);
(3)在“非常了解”防疫常识的学生中,某班有5个学生,其中3男2女,计划在这5个学生中随机抽选两个加入防疫志愿者团队,请用画树状图的方法求所选两个学生中至少有一个女生的概率.
解:(3)设3男生对应大写字母A,B,C,两女生对应大写字母D,E,在这5个学生中随机抽选两个加入防疫志愿者团队的所有结果,利用树状图呈现如下:
共有种等可能结果,满足所选两个学生中至少有一个女生有:种,
由概率公式得所选两个学生中至少有一个女生的概率为:.
【5-1】小燕一家三口在商场参加抽奖活动,每人只有一次抽奖机会:在一个不透明的箱子中装有红、黄、白三种球各1个,这些球除颜色外无其他差别,从箱子中随机摸出1个球,然后放回箱子中,轮到下一个人摸球,三人摸到球的颜色都不相同的概率是( )
A. B. C. D.
D
【5-2】甲、乙、丙三位学生进入了“校园朗诵比赛”冠军、亚军和季军的决赛,他们将通过抽签来决定比赛的出场顺序.
(1)求甲第一个出场的概率;
(2)求甲比乙先出场的概率.
解:画树状图如右图:
所有等可能的情况有6种,其中甲
第一个出场的情况有2种,则P(甲第一个出场)==.
(2)甲比乙先出场的情况有3种,则P(甲比乙先出场)==
【5-3】为了增加学生的阅读量,达到让学生“在阅读中成长,在成长中阅读”的效果,某中学计划在各班设立图书角.为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查.学校团委在收集整理了学生喜爱的书籍类型(A.科普、B.文学、C.体育、D.其他)数据后,绘制出两幅不完整的统计图,如图所示.
请你根据以上信息,解答下列问题.
(1)随机抽样调查的样本容量是______,扇形统计图中“B”所对应的圆心角的度数为______度;
(1)解:样本容量是:;
C所占的百分比为:;
∴扇形统计图中“B”所对应的圆心角的度数为:(1-25%-10%-35%)×360°=108°.
【5-3】为了增加学生的阅读量,达到让学生“在阅读中成长,在成长中阅读”的效果,某中学计划在各班设立图书角.为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查.学校团委在收集整理了学生喜爱的书籍类型(A.科普、B.文学、C.体育、D.其他)数据后,绘制出两幅不完整的统计图,如图所示.
请你根据以上信息,解答下列问题.
(2)补全条形统计图;
(2)解:D的数量为:,
B的数量为:;
补全条形图如右图:
(3)抽样中选择文学类书籍的学生有2名男生和2名女生,校团委计划从中随机抽取2名学生参加团委组织的征文大赛,求恰好抽出一男一女的概率.
解:由题意,树状图如下:
∴共有等可能事件12种可能,其中一男一女的有8种可能.
所以.
用频率估计概率
6
例9.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
例10.某水果公司以3元/kg的成本新进了20000kg雪梨,销售人员首先从所有的雪梨中随机地抽取若干千克,进行了“雪梨损坏率”统计,并把获得的数据记录在下表中(1)请你帮忙完成此表
(2)如果公司希望这些雪梨能够获得税前利润10000元,那么在出售雪梨(已去掉损坏的雪梨)时,大约每千克定价为多少元比较合适
解:由表可以看出,损坏的雪梨的频率稳定在0.1附近,
即可知雪梨的损坏率为0.1,则完好率为0.9,
则可知20000kg雪梨中完好的质量为: 20000×0.9=18000(kg)
完好雪梨的实际成本为:=≈3.33(元/kg)
设每千克雪梨的售价为x元,则(x-3.33)×18000=10000,解得x≈3.9
因此,出售雪梨时,每千克定价大约3.9元可获利润10000元.
【6-1】甲、乙两名同学在一次用频率去估计概率的实验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的实验可能是( )
A.从一装有2个白球和1个红球的袋子中任取
一球,取到红球的概率.
B.掷一枚正六面体的骰子,出现1点的概率
C.拋一枚硬币,出现正面的概率
D.任意写一个整数,它能被2整除的概率
A
【6-2】一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的反面是平的.将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下.由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某课外兴趣小组做了棋子下掷试验,试验数据如下表:
(1)请将数据表补充完整;
18
0.55
(2)画出“兵”字面朝上的频率分布折线图:
(3)如果试验继续进行下去,根据上表的数据,这个试验的频率将稳定在它的概率附近,请你估计这个概率是多少
解:(3)估计“兵”字面朝上的概率是0.55.
【6-3】某养鱼专业户在相同条件下,做鱼苗放养成活率试验.结果如下表所示,请先完成下表:(结果保留小数点后三位)
(1)由上表中数据估计:放养20000条鱼苗,约有_______条能成活;由此推测其成活率是______;
(2)过了一段时间后,养鱼人为了估计鱼塘中鱼的数目,先从塘中捕捞出n条鱼,并在每条鱼身上做好记号,放归鱼塘一段时间后,再从塘中捞出a条鱼,其中有m条带有记号,则可估计鱼塘中鱼的数目为______条.
18000
0.9
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
人教版九年级上册
概率初步章末小结
第二十五章 概率初步
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.梳理本章的知识要点,回顾与复习本章知识;
2.巩固并能熟练运用列举法、列表法和树状图法求概率;(重、难点)
3.能应用频率估计概率解决生活中的实际问题.
必然事件:在一定条件下,有些事件必然会发生,这样的事件称为必然事件.
不可能事件:在一定条件下,有些事件必然不会发生,这样的事件称为不可能事件.
确定性事件:必然事件与不可能事件统称确定性事件.
随机事件:在一定条件下,有些事件有可能发生,也有可能不发生,事先无法确定,这种事件称为随机事件.
一、事件的分类及其概念
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率P(A)= .
事件发生的可能性越大,它的概率越接近1;反之,事件发生的可能性越小,它的概率越接近0(如下图).
二、概率的概念
三、随机事件的概率的求法
1.直接列举法求随机事件的概率:
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,那么出现每一种结果的概率都是 .
如果事件A包括其中的m种可能的结果,那么事件A发生的概率
P(A)=
【适用范围】直接列举法比较适合用于最多涉及两个试验因素或分两步进行的试验,且事件总结果的种数比较少的等可能性事件.
三、随机事件的概率的求法
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
列表法中表格构造特点:
2.列表法求随机事件的概率:
三、随机事件的概率的求法
3.树状图法求随机事件的概率:
当一次试验中涉及2个因素或更多的因素时, 为了不重不漏地列出所有可能的结果,通常采用“树状图”.
画树状图求概率的基本步骤
(1)明确一次试验的几个步骤及顺序;
(2)画树状图列举一次试验的所有可能结果;
(3)数出随机事件A包含的结果数m,试验的所有可能结果数n;
(4)用概率公式进行计算.
三、随机事件的概率的求法
四、频率来估计概率
4.树状图法求随机事件的概率:
①当实验的所有结果不是有限个,或各种可能结果发生的可能性不相等时,我们用大量重复试验中随机事件发生的稳定频率来估计概率.
②频率与概率的关系:两者都能定量地反映随机事件可能性的大小,但频率具有随机性,概率是自身固有的性质,不具有随机性.
事件的分类
1
例1.投掷两枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,则下列事件为随机事件的是( )
A.两枚骰子向上一面的点数之和大于1
B.两枚骰子向上一面的点数之和等于1
C.两枚骰子向上一面的点数之和大于12
D.两枚骰子向上一面的点数之和等于12
D
事件的分类
1
例2.下列说法中正确的是( )
A.“任意画出一个等边三角形,它是轴对称图形”是随机事件
B.“任意画出一个平行四边形,它是中心对称图形”是必然事件
C.“概率为0.0001的事件”是不可能事件
D.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
B
【1-1】下列事件中,属于随机事件的是( )
A.买一张体育彩票中奖
B.太阳从西边落下
C.掷一枚质地均匀的正六面体骰子所得点数不超过6
D.口袋中装有10个红球,从中摸出一个白球
【1-2】下列成语所描述的事件是不可能事件的是( )
A.百步穿杨 B.瓮中捉鳖 C.水中捞月 D.守株待兔
【1-3】“一个不透明的袋子中装有3个小球,它们的标号分别为1,2,3,从中摸出1个小球,标号为“4”,这个事件是____________(填“必然事件”“不可能事件”或“随机事件”).
A
C
不可能事件
判断事件发生的可能性大小
2
例3.如图,转盘中个扇形的面积都相等,任意转动转盘次,当转盘停止转动时,估计下列个事件发生的可能性大小,其中事件发生的可能性最大的是( )
A.指针落在标有的区域内
B.指针落在标有的区域内
C.指针落在标有偶数或奇数的区域内
D.指针落在标有奇数的区域内
C
【2-1】质地均匀的骰子六个面分别刻有1到6的点数,掷两次骰子,得到向上一面的两个点数.则下列事件中,发生可能性最大的是( )
A.点数都是偶数 B.点数的和是奇数
C.点数的和小于12 D.点数的和大于10
C
【2-1】如图,转盘中5个扇形的面积都相等,任意转动转盘一次,当转盘停止转动时,把下列事件的序号按发生的可能性从小到大的顺序排列为______________.
①指针落在标有3的区域内;
②指针落在标有奇数的区域;
③指针落在标有6的区域内;
④指针落在标有偶数或奇数的区域.
③<①<②<④
【2-3】为了了解学生每月的零用钱情况,从甲、乙、丙三个学校各随机抽取200名学生,调查了他们的零用钱情况(单位:元)具体情况如下:
在调查过程中,从______(填“甲”,“乙”或“丙”)校随机抽取学生,抽到的学生“零用钱不低于300元”的可能性最大.
学校频数零 用钱 100≤x<200 200≤x<300 300≤x<400 400≤x<500 500以上 合计
甲 5 35 150 8 2 200
乙 16 54 68 52 10 200
丙 0 10 40 70 80 200
丙
用直接列举法求概率
3
例4.桌子上有三个不透明的盒子,小慧将一个白球放入其中一个大盒子,大鹏将一个黑球也随机放入一个盒子,则两个球不在同一个盒子里的概率为( )
A. B. C. D.
【分析】解:假设三个不透明的盒子分别为A,B,C,
当小慧把白球放入盒子A中,大鹏则可能把黑球放入A,B,C中;
当小慧把白球放入盒子B中,大鹏则可能把黑球放入A,B,C中;
当小慧把白球放入盒子C中,大鹏则可能把黑球放入A,B,C中;
根据概率定义可得所有等可能出现的结果数为9,其中两个球在同一盒子的事件数为3,分别为AA,BB,CC;
所以,两个球不在同一盒子的结果数为9-3=6,
所以,两个球不在同一个盒子里的概率为.
D
【3-1】若从长度分别为3、5、6、9的四条线段中任取三条,则能组成三角形的概率为( )
A. B. C. D.
A
【3-2】如图,随机闭合开关K1,K2,K3中的两个,则能让两盏灯泡同时发光的概率为( )
A. B. C. D.
B
用列表法求概率
4
例5.现有《北京冬奥会―雪上运动》纪念邮票4张.纪念邮票封面设计,分别是A越野滑雪;B高山滑雪;C冬季两项;D自由式滑雪(四张卡片除字母和图案内容外,其余完全相同).姐弟两人做游戏,他们将这四张卡片混在一起,背面朝上放好.若两人分别随机抽取一张卡片(不放回),请求出恰好姐姐抽到A越野滑雪,弟弟抽到B高山滑雪的概率.
A B C D
A / (A,B) (A,C) (A,D)
B (B,A) / (B,C) (B,D)
C (C,A) (C,B) / (C,D)
D (D,A) (D,B) (D,C) /
解:用列表法:
由表格可知:共有12种结果,并且它们的可能性相同,其中姐姐抽到A越野滑雪,弟弟抽到B高山滑雪的结果数为1.
(A越野滑雪B高山滑雪)=.
用列表法求概率
4
例6.今年猪肉价格受非洲猪瘟疫情影响,有较大幅度的上升,为了解某地区养殖户受非洲猪瘟疫情感染受灾情况,现从该地区建档的养殖户中随机抽取了部分养殖户进行了调查(把调查结果分为四个等级:A级:非常严重;B级:严重;C级:一般;D级:没有感染),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
(1)本次抽样调查的养殖户的总户数是______户;
把图2条形统计图补充完整.
(2)若该地区建档的养殖户有1500户,求非常严
重与严重的养殖户一共有多少户?
(3)某调研单位想从3户建档养殖户(分别记为a,
b,c)中随机选取两户,进一步跟踪监测病毒传
播情况,请用列表的方法求出选中养殖户c的概
率.
(1)解:总的户数:21÷35%=60(户),
“C级”的户数:60﹣9﹣21﹣9=21(户),
补全条形统计图如图所示:
(2)解:1500×=750(户),
答:若该地区建档的养殖户有1500户中“严重”和“非常严重”的养殖户一共有750户;
(3)解:用表格表示所有可能出现的情况如右图:
共有6种不同的情况,其中选中c的情况有4种,
∴即概率为:.
【4-1】小丽的爸爸积极参加社区防疫志愿服务,根据社区安排,志愿者将被随机分配到以下小组中的一个:A组(体温检测)、B组(环境消杀)、C组(便民代购)、D组(宣传巡查)开展服务工作.
(1)小丽的爸爸被分配到C组的概率是 ;
(2)若小丽的班主任刘老师也加入了该社区的志愿者队伍,那么刘老师和小丽的爸爸被分到同一组的概率是多少?请用列表的方法写出分析过程.
(2)解:列表如下:
小组 A B C D
A
B
C
D
因为一共有16种等可能的结果,其中刘老师和小丽的爸爸被分到同一组的有4种结果,所以P(两人被分到同一组).
答:刘老师和小丽的爸爸被分到同一组的概率是.
【4-2】在不透明的袋中有大小、形状和质地完全相同的小球,它们分别标有数字-1、-2、1、2,从袋中任意摸出一个小球(不放回),将袋中的小球搅匀后,再从袋中摸出另一个小球.
(1)请你表示摸出小球上的数字出现的所有结果;
解:(1)可能出现的所有结果如下:
∴共12种结果.
(2)若规定:如果摸出的两个小球上的数字都是方程x2-3x+2=0的根,则小明赢;如果摸出两个小球上的数字都不是x2-3x+2=0的根,则小亮赢.你认为这个游戏规则对小明、小亮公平吗 请说明理由.
解:(2)由方程x2-3x+2=0,解得,x1=1,x2=2
∴P(小明赢)= = ,P(小亮赢)= =
∴游戏公平.
【4-3】为了继续宣传新冠疫苗接种的重要性,某小区物业部门准备在已经接种疫苗的居民中招募2名志愿宣传者,现有2名男性2名女性共4名居民报名.请用列表的方法,求要从这4人中随机挑选2人,恰好抽到一名男性和一名女性的概率.
解:由题可列下表:
由表可知,共有12种等可能的结果,而两个人选中一名男性和一名女性的结果有8种,
∴.
用画树形图法求概率
5
例7.甲口袋中装有2个相同小球,它们分别写有数字1,2;乙口袋中装有3个相同小球,它们分别写有数字3,4,5;丙口袋中装有2个相同小球,它们分别写有数字6,7.从三个口袋各随机取出1个小球.用画树状图求:
(1)取出的3个小球上恰好有一个偶数的概率;
(2)取出的3个小球上全是奇数的概率.
解:画树状图为:
共有12种等可能的结果,其中取出的3个小球,上恰好有一个偶数的结果数为5,所以取出的3个小球5上恰好有一个偶数的概率=
(2)取出的3个小球上全是奇数的结果数为2,所2.以取出的3个小球.上全是奇数的概率==
用画树形图法求概率
5
例8.某校开展主题为“防疫常识知多少”的调查活动,抽取了部分学生进行调查,调查问卷设置了:非常了解、:比较了解、:基本了解、:不太了解四个等级,要求每个学生填且只能填其中的一个等级,采取随机抽样的方式,并根据调查结果绘制成如图所示不完整的频数分布表和统计图,根据以上信息回答下列问题:
等级 频数 频率
20 0.4
15
10 0.2
0.1
(1)频数分布表中_____,_____,将统计图补充完整;
解:(1)被调查的总人数为:
(人),
(人),
,
(2)若该校有学生1000人,请根据抽样调查结果估算该校“非常了解”和“比较了解”防疫常识的学生共有多少人?
解:(2)根据频数分布表知,“非常了解”和“比较了解”的频率之和为:,
利用样本估计总体的思想,若该校有学生1000人,校“非常了解”和“比较了解”防疫常识的学生共有:(人);
(3)在“非常了解”防疫常识的学生中,某班有5个学生,其中3男2女,计划在这5个学生中随机抽选两个加入防疫志愿者团队,请用画树状图的方法求所选两个学生中至少有一个女生的概率.
解:(3)设3男生对应大写字母A,B,C,两女生对应大写字母D,E,在这5个学生中随机抽选两个加入防疫志愿者团队的所有结果,利用树状图呈现如下:
共有种等可能结果,满足所选两个学生中至少有一个女生有:种,
由概率公式得所选两个学生中至少有一个女生的概率为:.
【5-1】小燕一家三口在商场参加抽奖活动,每人只有一次抽奖机会:在一个不透明的箱子中装有红、黄、白三种球各1个,这些球除颜色外无其他差别,从箱子中随机摸出1个球,然后放回箱子中,轮到下一个人摸球,三人摸到球的颜色都不相同的概率是( )
A. B. C. D.
D
【5-2】甲、乙、丙三位学生进入了“校园朗诵比赛”冠军、亚军和季军的决赛,他们将通过抽签来决定比赛的出场顺序.
(1)求甲第一个出场的概率;
(2)求甲比乙先出场的概率.
解:画树状图如右图:
所有等可能的情况有6种,其中甲
第一个出场的情况有2种,则P(甲第一个出场)==.
(2)甲比乙先出场的情况有3种,则P(甲比乙先出场)==
【5-3】为了增加学生的阅读量,达到让学生“在阅读中成长,在成长中阅读”的效果,某中学计划在各班设立图书角.为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查.学校团委在收集整理了学生喜爱的书籍类型(A.科普、B.文学、C.体育、D.其他)数据后,绘制出两幅不完整的统计图,如图所示.
请你根据以上信息,解答下列问题.
(1)随机抽样调查的样本容量是______,扇形统计图中“B”所对应的圆心角的度数为______度;
(1)解:样本容量是:;
C所占的百分比为:;
∴扇形统计图中“B”所对应的圆心角的度数为:(1-25%-10%-35%)×360°=108°.
【5-3】为了增加学生的阅读量,达到让学生“在阅读中成长,在成长中阅读”的效果,某中学计划在各班设立图书角.为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查.学校团委在收集整理了学生喜爱的书籍类型(A.科普、B.文学、C.体育、D.其他)数据后,绘制出两幅不完整的统计图,如图所示.
请你根据以上信息,解答下列问题.
(2)补全条形统计图;
(2)解:D的数量为:,
B的数量为:;
补全条形图如右图:
(3)抽样中选择文学类书籍的学生有2名男生和2名女生,校团委计划从中随机抽取2名学生参加团委组织的征文大赛,求恰好抽出一男一女的概率.
解:由题意,树状图如下:
∴共有等可能事件12种可能,其中一男一女的有8种可能.
所以.
用频率估计概率
6
例9.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
例10.某水果公司以3元/kg的成本新进了20000kg雪梨,销售人员首先从所有的雪梨中随机地抽取若干千克,进行了“雪梨损坏率”统计,并把获得的数据记录在下表中(1)请你帮忙完成此表
(2)如果公司希望这些雪梨能够获得税前利润10000元,那么在出售雪梨(已去掉损坏的雪梨)时,大约每千克定价为多少元比较合适
解:由表可以看出,损坏的雪梨的频率稳定在0.1附近,
即可知雪梨的损坏率为0.1,则完好率为0.9,
则可知20000kg雪梨中完好的质量为: 20000×0.9=18000(kg)
完好雪梨的实际成本为:=≈3.33(元/kg)
设每千克雪梨的售价为x元,则(x-3.33)×18000=10000,解得x≈3.9
因此,出售雪梨时,每千克定价大约3.9元可获利润10000元.
【6-1】甲、乙两名同学在一次用频率去估计概率的实验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的实验可能是( )
A.从一装有2个白球和1个红球的袋子中任取
一球,取到红球的概率.
B.掷一枚正六面体的骰子,出现1点的概率
C.拋一枚硬币,出现正面的概率
D.任意写一个整数,它能被2整除的概率
A
【6-2】一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的反面是平的.将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下.由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某课外兴趣小组做了棋子下掷试验,试验数据如下表:
(1)请将数据表补充完整;
18
0.55
(2)画出“兵”字面朝上的频率分布折线图:
(3)如果试验继续进行下去,根据上表的数据,这个试验的频率将稳定在它的概率附近,请你估计这个概率是多少
解:(3)估计“兵”字面朝上的概率是0.55.
【6-3】某养鱼专业户在相同条件下,做鱼苗放养成活率试验.结果如下表所示,请先完成下表:(结果保留小数点后三位)
(1)由上表中数据估计:放养20000条鱼苗,约有_______条能成活;由此推测其成活率是______;
(2)过了一段时间后,养鱼人为了估计鱼塘中鱼的数目,先从塘中捕捞出n条鱼,并在每条鱼身上做好记号,放归鱼塘一段时间后,再从塘中捞出a条鱼,其中有m条带有记号,则可估计鱼塘中鱼的数目为______条.
18000
0.9
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
