25.2.1 运用直接列举或列表法求概率 优质课件(33张PPT)
文档属性
| 名称 | 25.2.1 运用直接列举或列表法求概率 优质课件(33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 09:34:06 | ||
图片预览










文档简介
(共33张PPT)
九上数学同步优质课件
人教版九年级上册
运用直接列举或列表法求概率
第二十五章 概率初步
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.知道什么时候采用“直接列举法”和“列表法” .
2.会正确“列表”表示出所有可能出现的结果.(难点)
3.知道如何利用“列表法”求随机事件的概率.(重点)
一个家庭有两个孩子,从出生的先后顺序和性别上来分,有多少种可能出现的情况?
例1.同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
解:列举抛掷两枚硬币所能产生的全部结果,它们是:正正、正反、反正、反反.
所有可能的结果共有4种,并且这4种结果出现的可能性相等.
例1.同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
解:列举抛掷两枚硬币所能产生的全部结果,它们是:正正、正反、反正、反反.
(1)所有可能的结果中,满足两枚硬币全部正面向上(记为事件A)的结果只有一种,即“正正”,
P(A)=
所以
例1.同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
解:列举抛掷两枚硬币所能产生的全部结果,它们是:正正、正反、反正、反反.
(2)满足两枚硬币全部反面向上(记为事件B)的结果也只有1种,即“反反”,
P(B)=
所以
例1.同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
解:列举抛掷两枚硬币所能产生的全部结果,它们是:正正、正反、反正、反反.
(3)一枚硬币正面向上,一枚硬币反面向上(记为事件C)的结果共有2种,即“反正”“正反”,
P(C)=
所以
=
上述这种列举法我们称为直接列举法,即把事件可能出现的结果一一列出.
【适用范围】直接列举法比较适合用于最多涉及两个试验因素或分两步进行的试验,且事件总结果的种数比较少的等可能性事件.
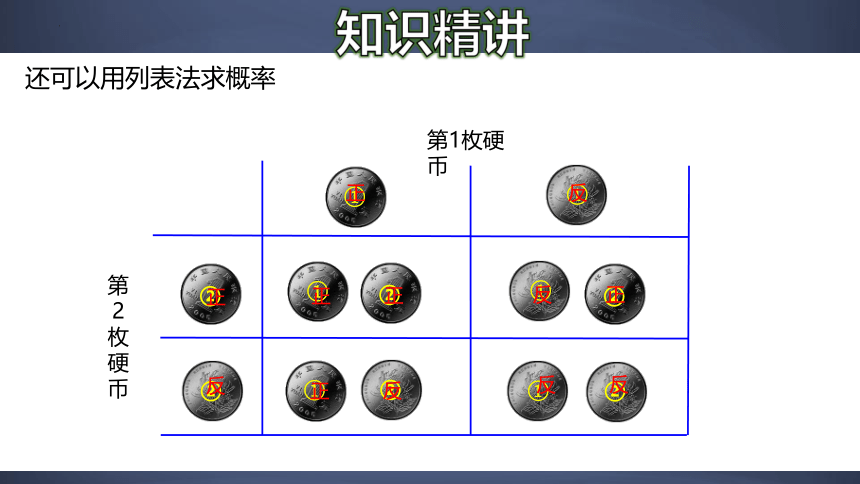
①
①
①
①
②
②
②
②
②
②
①
①
第1枚硬币
第
2
枚硬币
反
正
正
反
正
正
反
正
正
反
反
反
知识精讲
还可以用列表法求概率
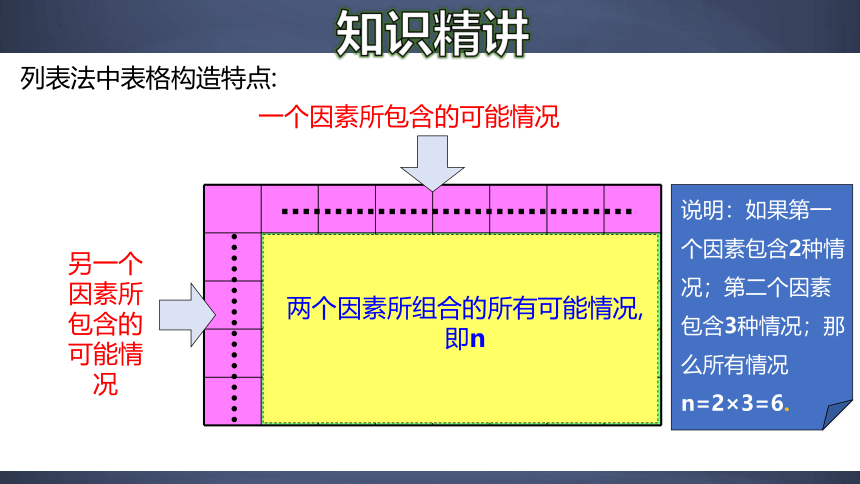
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
列表法中表格构造特点:
说明:如果第一个因素包含2种情况;第二个因素包含3种情况;那么所有情况n=2×3=6.
知识精讲
“同时抛掷两枚质地均匀的硬币”与“先后两次抛掷一枚质地均匀的硬币”,这两种试验的所有可能结果一样吗?
开始
第一掷
第二掷
所有可能出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
一样.
【点睛】随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与“一个随机事件先后两次发生”的结果是一样的.
不透明袋子中装有红、绿小球各一个,除颜色外无其它差别.随机摸出一个小球后,放回并摇匀,再随机摸出一个.求下列事件的概率:
(1)第一次摸到红球,第二次摸到绿球;
(2)两次都摸到相同颜色的小球;
(3)两次摸到的球中一个绿球、一个红球.
解:列举两次摸球所能产生的全部结果,它们是:红红,红绿,绿红,绿绿.这4种结果出现的可能性相等.
(1)满足第一次摸到红球,第二次摸到绿球(记为事件A)的结果只有1种,即“红绿”,所以 P(A)= ;
(2)满足两次都摸到相同颜色的小球(记为事件B)的结果共有2种,即“红红”,“绿绿”,所以 P(B)= ;
(3)满足两次摸到的球中一个绿球、一个红球(记为事件C)的结果共有2种,即“红绿”,“绿红”,所以 P(C)= .
例2.同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子点数的和是9;
(3)至少有一枚骰子的点数为2.
分析:当一次试验要涉及两个因素(掷两枚骰子),并且可能出现的结果数目较多时,为了不重不漏地列出所有可能的结果,通常采用列表法.
解:两枚骰子分别记为第一枚和第二枚,可以用下表列举出所有可能出现的结果.
由上表可以看出,同时掷两枚骰子,可能出现的结果有36种,它们出现的可能性相等.
解:两枚骰子分别记为第一枚和第二枚,可以用下表列举出所有可能出现的结果.
(1)两枚骰子的点数相同(记为事件A)的结果有6种(表中的红色部分),即(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),所以P(A)==
解:两枚骰子分别记为第一枚和第二枚,可以用下表列举出所有可能出现的结果.
(2)两枚骰子的点数和是9(记为事件B)的结果有4种(表中的阴影部分),即(3,6),(4,5),(5,4),(6,3),所以P(B)==.
解:两枚骰子分别记为第一枚和第二枚,可以用下表列举出所有可能出现的结果.
(3)至少有一枚骰子的点数为2(记为事件C)的结果有11种(表中的蓝色部分),所以P(C)=
【点睛】当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
如果把例2中的“同时掷两枚质地均匀的骰子”改为“把一枚质地均匀的骰子掷两次”,得到的结果有变化吗?为什么?
一样.
【点睛】随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与“一个随机事件先后两次发生”的结果是一样的.
有6张看上去无差别的卡片,上面分别写着1、2、3、4、5、6.随机抽取1张后,放回并混在一起,再随机抽取1张,那么第二次取出的数字能够整除第一次取出的数字的概率是多少?
解:列表:由右表可知
第二次取出的数字能够整除第一次取出的数字共有14种,
概率是: =
1.小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项那么两人同时选择“参加社会调查”的概率为( )
A. B. C. D.
2.有A,B两个不透明的口袋,每个口袋里装有两个相同的球,A袋中的两个球上分别写了“细”、“致”的字样,B袋中的两个球上分别写了“信”、“心”的字样,从每个口袋里各摸出一个球,刚好能组成“细心”字样的概率是( )
A. B. C. D.
A
B
3.若从长度分别为3、5、6、9的四条线段中任取三条,则能组成三角形的概率为( )
A. B. C. D.
4.学校组织校外实践活动,安排给九年级三辆车,小明与小红都可以从这三辆车中任选一辆搭乘,小明与小红同车的概率是( )
A. B. C. D.
A
C
5.如图,随机闭合开关K1,K2,K3中的两个,
则能让两盏灯泡同时发光的概率为( )
A. B. C. D.
6.甲、乙两同学掷一枚骰子,用字母p, q分别表示两人各投掷一次的点数,则满足关于x的方程x2+px+q=0有两个相等实数解的概率是( )
A. B. C. D.
B
D
7.在一个布袋里放有1个白球和2个红球,它们除颜色外其余都相同,从布袋里摸出1个球,记下颜色后放回,搅匀再摸出1个球.将2个红球分别记为红I,红ⅡI,两次摸球的所有可能的结果如表所示,则两次摸出的球都是红球的概率是_______.
8.从-2,-1,2这三个数中任取两个不同的数作为点的坐标,该点在第四象限的概率是______.
9.从数字1,2,3中任取两个不同数字组成一个两位数,则这个两位数大于21的概率是_______.
10.一套书共有上、中、下三册,将它们任意摆放到书架的同一层上,这三册书从左向右恰好成上、中、下顺序的概率是_______.
11.小明和弟弟在玩猜点数的游戏,规则是这样的:将红桃A至红桃5、黑桃A至黑桃5两组扑克牌分别洗匀,每次从两种花色中各抽出一张,抽后并放回洗匀,在抽之前猜一个数,如果每次抽出的两张牌的点数之和与猜的数相同算对,否则算错,谁猜对的多算赢.小明每次说的数不是4就是5;弟弟每次说的数不是6就是7,那么谁赢的可能大呢 为什么
解:两次抽牌的牌面点数和,所有可能出现的结果如下表:
由上表可知,牌面点数和为6的概率是,而牌面点数和为5或7的概率都是,牌面点数和为4的概率是,所以弟弟赢的可能性大.
12.在不透明的袋中有大小、形状和质地完全相同的小球,它们分别标有数字-1、-2、1、2,从袋中任意摸出一个小球(不放回),将袋中的小球搅匀后,再从袋中摸出另一个小球.
(1)请你表示摸出小球上的数字出现的所有结果;
解:(1)可能出现的所有结果如下:
∴共12种结果.
(2)若规定:如果摸出的两个小球上的数字都是方程x2-3x+2=0的根,则小明赢;如果摸出两个小球上的数字都不是x2-3x+2=0的根,则小亮赢.你认为这个游戏规则对小明、小亮公平吗 请说明理由.
解:(2)由方程x2-3x+2=0,解得,x1=1,x2=2
∴P(小明赢)= = ,P(小亮赢)= =
∴游戏公平.
小结梳理
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
人教版九年级上册
运用直接列举或列表法求概率
第二十五章 概率初步
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.知道什么时候采用“直接列举法”和“列表法” .
2.会正确“列表”表示出所有可能出现的结果.(难点)
3.知道如何利用“列表法”求随机事件的概率.(重点)
一个家庭有两个孩子,从出生的先后顺序和性别上来分,有多少种可能出现的情况?
例1.同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
解:列举抛掷两枚硬币所能产生的全部结果,它们是:正正、正反、反正、反反.
所有可能的结果共有4种,并且这4种结果出现的可能性相等.
例1.同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
解:列举抛掷两枚硬币所能产生的全部结果,它们是:正正、正反、反正、反反.
(1)所有可能的结果中,满足两枚硬币全部正面向上(记为事件A)的结果只有一种,即“正正”,
P(A)=
所以
例1.同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
解:列举抛掷两枚硬币所能产生的全部结果,它们是:正正、正反、反正、反反.
(2)满足两枚硬币全部反面向上(记为事件B)的结果也只有1种,即“反反”,
P(B)=
所以
例1.同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
解:列举抛掷两枚硬币所能产生的全部结果,它们是:正正、正反、反正、反反.
(3)一枚硬币正面向上,一枚硬币反面向上(记为事件C)的结果共有2种,即“反正”“正反”,
P(C)=
所以
=
上述这种列举法我们称为直接列举法,即把事件可能出现的结果一一列出.
【适用范围】直接列举法比较适合用于最多涉及两个试验因素或分两步进行的试验,且事件总结果的种数比较少的等可能性事件.
①
①
①
①
②
②
②
②
②
②
①
①
第1枚硬币
第
2
枚硬币
反
正
正
反
正
正
反
正
正
反
反
反
知识精讲
还可以用列表法求概率
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
列表法中表格构造特点:
说明:如果第一个因素包含2种情况;第二个因素包含3种情况;那么所有情况n=2×3=6.
知识精讲
“同时抛掷两枚质地均匀的硬币”与“先后两次抛掷一枚质地均匀的硬币”,这两种试验的所有可能结果一样吗?
开始
第一掷
第二掷
所有可能出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
一样.
【点睛】随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与“一个随机事件先后两次发生”的结果是一样的.
不透明袋子中装有红、绿小球各一个,除颜色外无其它差别.随机摸出一个小球后,放回并摇匀,再随机摸出一个.求下列事件的概率:
(1)第一次摸到红球,第二次摸到绿球;
(2)两次都摸到相同颜色的小球;
(3)两次摸到的球中一个绿球、一个红球.
解:列举两次摸球所能产生的全部结果,它们是:红红,红绿,绿红,绿绿.这4种结果出现的可能性相等.
(1)满足第一次摸到红球,第二次摸到绿球(记为事件A)的结果只有1种,即“红绿”,所以 P(A)= ;
(2)满足两次都摸到相同颜色的小球(记为事件B)的结果共有2种,即“红红”,“绿绿”,所以 P(B)= ;
(3)满足两次摸到的球中一个绿球、一个红球(记为事件C)的结果共有2种,即“红绿”,“绿红”,所以 P(C)= .
例2.同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子点数的和是9;
(3)至少有一枚骰子的点数为2.
分析:当一次试验要涉及两个因素(掷两枚骰子),并且可能出现的结果数目较多时,为了不重不漏地列出所有可能的结果,通常采用列表法.
解:两枚骰子分别记为第一枚和第二枚,可以用下表列举出所有可能出现的结果.
由上表可以看出,同时掷两枚骰子,可能出现的结果有36种,它们出现的可能性相等.
解:两枚骰子分别记为第一枚和第二枚,可以用下表列举出所有可能出现的结果.
(1)两枚骰子的点数相同(记为事件A)的结果有6种(表中的红色部分),即(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),所以P(A)==
解:两枚骰子分别记为第一枚和第二枚,可以用下表列举出所有可能出现的结果.
(2)两枚骰子的点数和是9(记为事件B)的结果有4种(表中的阴影部分),即(3,6),(4,5),(5,4),(6,3),所以P(B)==.
解:两枚骰子分别记为第一枚和第二枚,可以用下表列举出所有可能出现的结果.
(3)至少有一枚骰子的点数为2(记为事件C)的结果有11种(表中的蓝色部分),所以P(C)=
【点睛】当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
如果把例2中的“同时掷两枚质地均匀的骰子”改为“把一枚质地均匀的骰子掷两次”,得到的结果有变化吗?为什么?
一样.
【点睛】随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与“一个随机事件先后两次发生”的结果是一样的.
有6张看上去无差别的卡片,上面分别写着1、2、3、4、5、6.随机抽取1张后,放回并混在一起,再随机抽取1张,那么第二次取出的数字能够整除第一次取出的数字的概率是多少?
解:列表:由右表可知
第二次取出的数字能够整除第一次取出的数字共有14种,
概率是: =
1.小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项那么两人同时选择“参加社会调查”的概率为( )
A. B. C. D.
2.有A,B两个不透明的口袋,每个口袋里装有两个相同的球,A袋中的两个球上分别写了“细”、“致”的字样,B袋中的两个球上分别写了“信”、“心”的字样,从每个口袋里各摸出一个球,刚好能组成“细心”字样的概率是( )
A. B. C. D.
A
B
3.若从长度分别为3、5、6、9的四条线段中任取三条,则能组成三角形的概率为( )
A. B. C. D.
4.学校组织校外实践活动,安排给九年级三辆车,小明与小红都可以从这三辆车中任选一辆搭乘,小明与小红同车的概率是( )
A. B. C. D.
A
C
5.如图,随机闭合开关K1,K2,K3中的两个,
则能让两盏灯泡同时发光的概率为( )
A. B. C. D.
6.甲、乙两同学掷一枚骰子,用字母p, q分别表示两人各投掷一次的点数,则满足关于x的方程x2+px+q=0有两个相等实数解的概率是( )
A. B. C. D.
B
D
7.在一个布袋里放有1个白球和2个红球,它们除颜色外其余都相同,从布袋里摸出1个球,记下颜色后放回,搅匀再摸出1个球.将2个红球分别记为红I,红ⅡI,两次摸球的所有可能的结果如表所示,则两次摸出的球都是红球的概率是_______.
8.从-2,-1,2这三个数中任取两个不同的数作为点的坐标,该点在第四象限的概率是______.
9.从数字1,2,3中任取两个不同数字组成一个两位数,则这个两位数大于21的概率是_______.
10.一套书共有上、中、下三册,将它们任意摆放到书架的同一层上,这三册书从左向右恰好成上、中、下顺序的概率是_______.
11.小明和弟弟在玩猜点数的游戏,规则是这样的:将红桃A至红桃5、黑桃A至黑桃5两组扑克牌分别洗匀,每次从两种花色中各抽出一张,抽后并放回洗匀,在抽之前猜一个数,如果每次抽出的两张牌的点数之和与猜的数相同算对,否则算错,谁猜对的多算赢.小明每次说的数不是4就是5;弟弟每次说的数不是6就是7,那么谁赢的可能大呢 为什么
解:两次抽牌的牌面点数和,所有可能出现的结果如下表:
由上表可知,牌面点数和为6的概率是,而牌面点数和为5或7的概率都是,牌面点数和为4的概率是,所以弟弟赢的可能性大.
12.在不透明的袋中有大小、形状和质地完全相同的小球,它们分别标有数字-1、-2、1、2,从袋中任意摸出一个小球(不放回),将袋中的小球搅匀后,再从袋中摸出另一个小球.
(1)请你表示摸出小球上的数字出现的所有结果;
解:(1)可能出现的所有结果如下:
∴共12种结果.
(2)若规定:如果摸出的两个小球上的数字都是方程x2-3x+2=0的根,则小明赢;如果摸出两个小球上的数字都不是x2-3x+2=0的根,则小亮赢.你认为这个游戏规则对小明、小亮公平吗 请说明理由.
解:(2)由方程x2-3x+2=0,解得,x1=1,x2=2
∴P(小明赢)= = ,P(小亮赢)= =
∴游戏公平.
小结梳理
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
