25.2.2 画树状图法求概率 优质课件(共29张PPT)
文档属性
| 名称 | 25.2.2 画树状图法求概率 优质课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-28 11:44:28 | ||
图片预览





文档简介
(共29张PPT)
九上数学同步优质课件
人教版九年级上册
画树状图法求概率
第二十五章 概率初步
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.进一步理解等可能事件概率的意义;
2.学习运用树状图计算事件的概率(重点);
3.会正确用画树状图法求出所有可能出现的结果,并计算事件的概率.(难点)
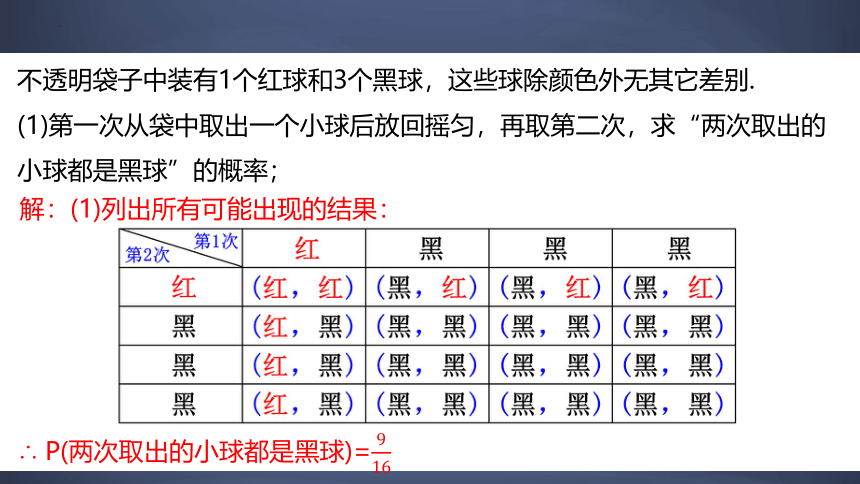
不透明袋子中装有1个红球和3个黑球,这些球除颜色外无其它差别.
(1)第一次从袋中取出一个小球后放回摇匀,再取第二次,求“两次取出的小球都是黑球”的概率;
解:(1)列出所有可能出现的结果:
∴ P(两次取出的小球都是黑球)=
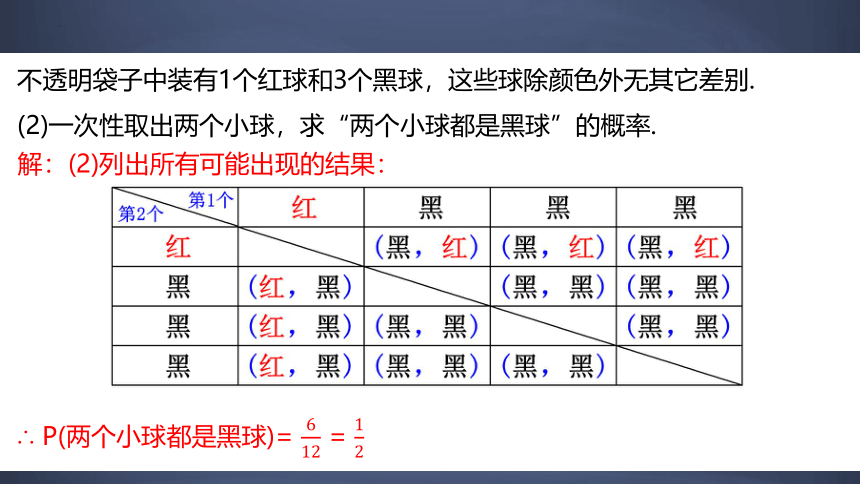
不透明袋子中装有1个红球和3个黑球,这些球除颜色外无其它差别.
(2)一次性取出两个小球,求“两个小球都是黑球”的概率.
解:(2)列出所有可能出现的结果:
∴ P(两个小球都是黑球)= =
例1.甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I. 从三个口袋中各随机地取出1个小球.
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少? (2)取出的3个小球上全是辅音字母的概率是多少?
分析:当一次试验要涉及3个或更多的因素(从3个口袋中取球)时,列表法就不方便了,为不重不漏地列出所有可能的结果,通常采用画树状图法.
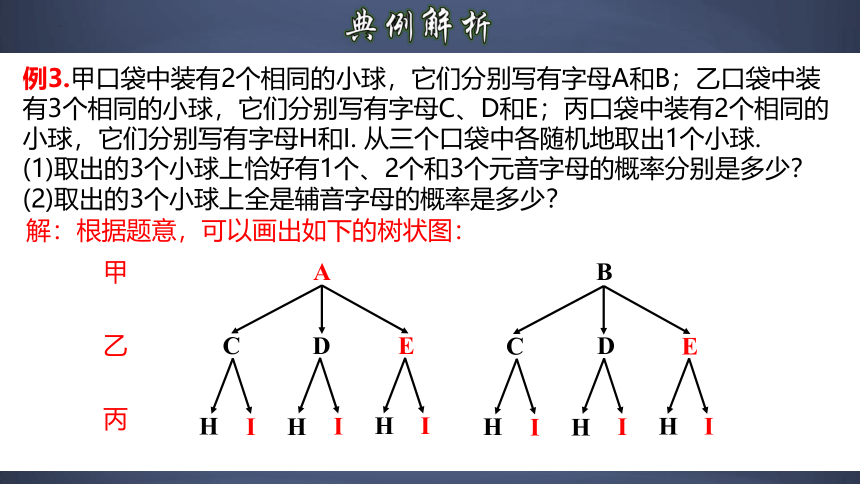
例3.甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I. 从三个口袋中各随机地取出1个小球.
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少? (2)取出的3个小球上全是辅音字母的概率是多少?
解:根据题意,可以画出如下的树状图:
甲
乙
丙
A
B
E
C
D
E
C
D
I
H
I
H
I
H
I
H
I
H
I
H
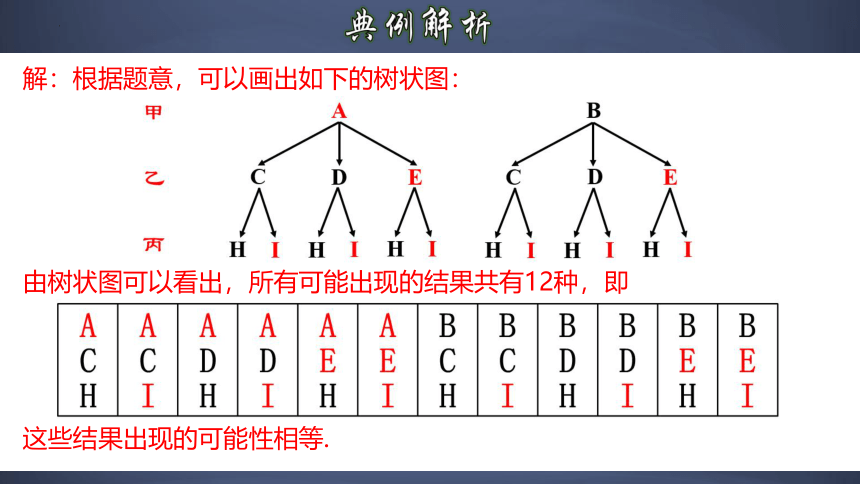
解:根据题意,可以画出如下的树状图:
由树状图可以看出,所有可能出现的结果共有12种,即
这些结果出现的可能性相等.
解:(1)只有1个元音字母的结果有5种,所以P(1个元音)= ;
有2个元音字母的结果有4种,所以P(2个元音)= ;
全部为元音字母的结果只有1种,所以P(3个元音)= ;
(2)全是辅音字母的结果有2种,所以P(3个辅音)= .
画树状图求概率的基本步骤
(1)明确一次试验的几个步骤及顺序;
(2)画树状图列举一次试验的所有可能结果;
(3)数出随机事件A包含的结果数m,试验的所有可能结果数n;
(4)用概率公式进行计算.
经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左转.
解:根据题意,可以画出如下的树状图:
由树状图可以看出,所有可能出现的结果共有27种.
因此,
(1) P(三辆车全部继续直行)=
(2) P(两辆车向右转,一辆车向左转)==
(3) P(至少有两辆车向左转)=
例2.甲、乙、丙三人做传球的游戏,开始时,球在甲手中,每次传球,持球的人将球任意传给其余两人中的一人,如此传球三次.
(1)写出三次传球的所有可能结果(即传球的方式);
(2)指定事件A:“传球三次后,球又回到甲的手中”,写出A发生的所有可能结果;
(3)求P(A).
共有八种可能的结果,每种结果出现的可能性相同;
(2)传球三次后,球又回到甲手中,事件A发生有两种可能出现结果(乙,丙,甲)(丙,乙,甲)
(3)P(A)=
解:(1)画树状图如下:
1.某校开展“文明小卫士”活动,从学生会“督查部”的3名学生(2男1女)中随机选2名进行督导,恰好选中2名男学生的概率是( )
A. B. C. D.
2.在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球1个,红球2个,摸出一个球不放回,再摸出一个球,两次都摸到红球的概率是( )
A. B. C. D.
A
C
3.在-2,-1,0,1,2这五个数中任取两数m,n,则抛物线y=(x-m)2+n的顶点在坐标轴上的概率为( )
A. B. C. D.
4.将一个篮球和一个足球随机放入三个不同的篮子中,则恰有一个篮子为空的概率为( )
A. B. C. D.
B
D
5.学生甲与学生乙玩一种转盘游戏.如图是两个完全相同的转盘,每个转盘被分成面积相等的四个区域,分别用数字“1”、“2”、“3”、“4”表示.固定指针,同时转动两个转盘,任其自由停止,若两指针所指数字的积为奇数,则甲获胜;若两指针所指数字的积为偶数,则乙获胜;若指针指向扇形的分界线,则都重转一次.在该游戏中乙获胜的概率是( )
A. B. C. D.
C
6.随机掷一枚质地均匀的硬币三次,则至少有一次正面朝上的概率是_____.
7.三名运动员参加定点投篮比赛,原定出场顺序是:甲第一个出场,乙第二个出场,丙第三个出场,由于某种原因,要求这三名运动员用抽签方式重新确定出场顺序,则抽签后每个运动员的出场顺序都发生变化的概率为_____.
8.游戏者同时转动A、B两个转盘进行“配紫色”游戏,求游戏者获胜的概率.
(在绘画过程中红色颜料与蓝色颜料混合就能配出紫色的颜料)
请你用列表法或树状图法红黄蓝解答本题.
8.游戏者同时转动A、B两个转盘进行“配紫色”游戏,求游戏者获胜的概率.
(在绘画过程中红色颜料与蓝色颜料混合就能配出紫色的颜料)
请你用列表法或树状图法红黄蓝解答本题.
解:列表如下:
P(配紫色)=
8.游戏者同时转动A、B两个转盘进行“配紫色”游戏,求游戏者获胜的概率.
(在绘画过程中红色颜料与蓝色颜料混合就能配出紫色的颜料)
请你用列表法或树状图法红黄蓝解答本题.
解:画树状图如下:
P(配紫色)=
9.甲口袋中装有两个相同的小球,它们的标号分别为2和7,乙口袋中装有两个相同的小球,它们的标号分别为4和5,丙口袋中装有三个相同的小球,它们的标号分别为3,8,9.从这3个口袋中各随机地取出1个小球.
(1)求取出的3个小球的标号全是奇数的概率是多少
解:(1)画树状图得:
∴一共有12种等可能的结果,其中,取出的3个小球的标号全是奇数的有2种.
∴取出的3个小球的标号全是奇数的概率是:P==.
9.甲口袋中装有两个相同的小球,它们的标号分别为2和7,乙口袋中装有两个相同的小球,它们的标号分别为4和5,丙口袋中装有三个相同的小球,它们的标号分别为3,8,9.从这3个口袋中各随机地取出1个小球.
(2)以取出的三个小球的标号分别表示三条线段的长度,求这些线段能构成三角形的概率.
解:(2)∵这些线段能构成三角形的有:[2、4、3],[7、4、8],[7、4、9],[7、5、3],[7、5、8],[7、5、9]共6种.
这些线段能构成三角形的概率是:P==.
10.小赵、小钱、小孙三人玩“剪刀、石头、布”的游戏,游戏规则如下:①石头赢剪刀,剪刀赢布,布赢石头;②两人游戏时,出相同的手势为平局;③多人游戏时都出相同的手势或者三种手势都出现为平局.请你解答:
(1)若其中两人玩“剪刀、石头、布”的游戏,玩一次合好平局的概率为___.
(2)求三人玩“剪刀、石头、布”一次恰好平局的概率.
(2)求三人玩“剪刀、石头、布”一次恰好平局的概率.
解:画树状图如图所示.
共有27种等可能的结果,其中三人玩“剪刀、石头、布”一次恰好平局的结果有9种.
∴三人玩“剪刀、石头、布”一次恰好平局的概率为
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
人教版九年级上册
画树状图法求概率
第二十五章 概率初步
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.进一步理解等可能事件概率的意义;
2.学习运用树状图计算事件的概率(重点);
3.会正确用画树状图法求出所有可能出现的结果,并计算事件的概率.(难点)
不透明袋子中装有1个红球和3个黑球,这些球除颜色外无其它差别.
(1)第一次从袋中取出一个小球后放回摇匀,再取第二次,求“两次取出的小球都是黑球”的概率;
解:(1)列出所有可能出现的结果:
∴ P(两次取出的小球都是黑球)=
不透明袋子中装有1个红球和3个黑球,这些球除颜色外无其它差别.
(2)一次性取出两个小球,求“两个小球都是黑球”的概率.
解:(2)列出所有可能出现的结果:
∴ P(两个小球都是黑球)= =
例1.甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I. 从三个口袋中各随机地取出1个小球.
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少? (2)取出的3个小球上全是辅音字母的概率是多少?
分析:当一次试验要涉及3个或更多的因素(从3个口袋中取球)时,列表法就不方便了,为不重不漏地列出所有可能的结果,通常采用画树状图法.
例3.甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I. 从三个口袋中各随机地取出1个小球.
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少? (2)取出的3个小球上全是辅音字母的概率是多少?
解:根据题意,可以画出如下的树状图:
甲
乙
丙
A
B
E
C
D
E
C
D
I
H
I
H
I
H
I
H
I
H
I
H
解:根据题意,可以画出如下的树状图:
由树状图可以看出,所有可能出现的结果共有12种,即
这些结果出现的可能性相等.
解:(1)只有1个元音字母的结果有5种,所以P(1个元音)= ;
有2个元音字母的结果有4种,所以P(2个元音)= ;
全部为元音字母的结果只有1种,所以P(3个元音)= ;
(2)全是辅音字母的结果有2种,所以P(3个辅音)= .
画树状图求概率的基本步骤
(1)明确一次试验的几个步骤及顺序;
(2)画树状图列举一次试验的所有可能结果;
(3)数出随机事件A包含的结果数m,试验的所有可能结果数n;
(4)用概率公式进行计算.
经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左转.
解:根据题意,可以画出如下的树状图:
由树状图可以看出,所有可能出现的结果共有27种.
因此,
(1) P(三辆车全部继续直行)=
(2) P(两辆车向右转,一辆车向左转)==
(3) P(至少有两辆车向左转)=
例2.甲、乙、丙三人做传球的游戏,开始时,球在甲手中,每次传球,持球的人将球任意传给其余两人中的一人,如此传球三次.
(1)写出三次传球的所有可能结果(即传球的方式);
(2)指定事件A:“传球三次后,球又回到甲的手中”,写出A发生的所有可能结果;
(3)求P(A).
共有八种可能的结果,每种结果出现的可能性相同;
(2)传球三次后,球又回到甲手中,事件A发生有两种可能出现结果(乙,丙,甲)(丙,乙,甲)
(3)P(A)=
解:(1)画树状图如下:
1.某校开展“文明小卫士”活动,从学生会“督查部”的3名学生(2男1女)中随机选2名进行督导,恰好选中2名男学生的概率是( )
A. B. C. D.
2.在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球1个,红球2个,摸出一个球不放回,再摸出一个球,两次都摸到红球的概率是( )
A. B. C. D.
A
C
3.在-2,-1,0,1,2这五个数中任取两数m,n,则抛物线y=(x-m)2+n的顶点在坐标轴上的概率为( )
A. B. C. D.
4.将一个篮球和一个足球随机放入三个不同的篮子中,则恰有一个篮子为空的概率为( )
A. B. C. D.
B
D
5.学生甲与学生乙玩一种转盘游戏.如图是两个完全相同的转盘,每个转盘被分成面积相等的四个区域,分别用数字“1”、“2”、“3”、“4”表示.固定指针,同时转动两个转盘,任其自由停止,若两指针所指数字的积为奇数,则甲获胜;若两指针所指数字的积为偶数,则乙获胜;若指针指向扇形的分界线,则都重转一次.在该游戏中乙获胜的概率是( )
A. B. C. D.
C
6.随机掷一枚质地均匀的硬币三次,则至少有一次正面朝上的概率是_____.
7.三名运动员参加定点投篮比赛,原定出场顺序是:甲第一个出场,乙第二个出场,丙第三个出场,由于某种原因,要求这三名运动员用抽签方式重新确定出场顺序,则抽签后每个运动员的出场顺序都发生变化的概率为_____.
8.游戏者同时转动A、B两个转盘进行“配紫色”游戏,求游戏者获胜的概率.
(在绘画过程中红色颜料与蓝色颜料混合就能配出紫色的颜料)
请你用列表法或树状图法红黄蓝解答本题.
8.游戏者同时转动A、B两个转盘进行“配紫色”游戏,求游戏者获胜的概率.
(在绘画过程中红色颜料与蓝色颜料混合就能配出紫色的颜料)
请你用列表法或树状图法红黄蓝解答本题.
解:列表如下:
P(配紫色)=
8.游戏者同时转动A、B两个转盘进行“配紫色”游戏,求游戏者获胜的概率.
(在绘画过程中红色颜料与蓝色颜料混合就能配出紫色的颜料)
请你用列表法或树状图法红黄蓝解答本题.
解:画树状图如下:
P(配紫色)=
9.甲口袋中装有两个相同的小球,它们的标号分别为2和7,乙口袋中装有两个相同的小球,它们的标号分别为4和5,丙口袋中装有三个相同的小球,它们的标号分别为3,8,9.从这3个口袋中各随机地取出1个小球.
(1)求取出的3个小球的标号全是奇数的概率是多少
解:(1)画树状图得:
∴一共有12种等可能的结果,其中,取出的3个小球的标号全是奇数的有2种.
∴取出的3个小球的标号全是奇数的概率是:P==.
9.甲口袋中装有两个相同的小球,它们的标号分别为2和7,乙口袋中装有两个相同的小球,它们的标号分别为4和5,丙口袋中装有三个相同的小球,它们的标号分别为3,8,9.从这3个口袋中各随机地取出1个小球.
(2)以取出的三个小球的标号分别表示三条线段的长度,求这些线段能构成三角形的概率.
解:(2)∵这些线段能构成三角形的有:[2、4、3],[7、4、8],[7、4、9],[7、5、3],[7、5、8],[7、5、9]共6种.
这些线段能构成三角形的概率是:P==.
10.小赵、小钱、小孙三人玩“剪刀、石头、布”的游戏,游戏规则如下:①石头赢剪刀,剪刀赢布,布赢石头;②两人游戏时,出相同的手势为平局;③多人游戏时都出相同的手势或者三种手势都出现为平局.请你解答:
(1)若其中两人玩“剪刀、石头、布”的游戏,玩一次合好平局的概率为___.
(2)求三人玩“剪刀、石头、布”一次恰好平局的概率.
(2)求三人玩“剪刀、石头、布”一次恰好平局的概率.
解:画树状图如图所示.
共有27种等可能的结果,其中三人玩“剪刀、石头、布”一次恰好平局的结果有9种.
∴三人玩“剪刀、石头、布”一次恰好平局的概率为
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
