第7课 分式的加减(含答案)[下学期]
文档属性
| 名称 | 第7课 分式的加减(含答案)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 79.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-25 12:39:00 | ||
图片预览


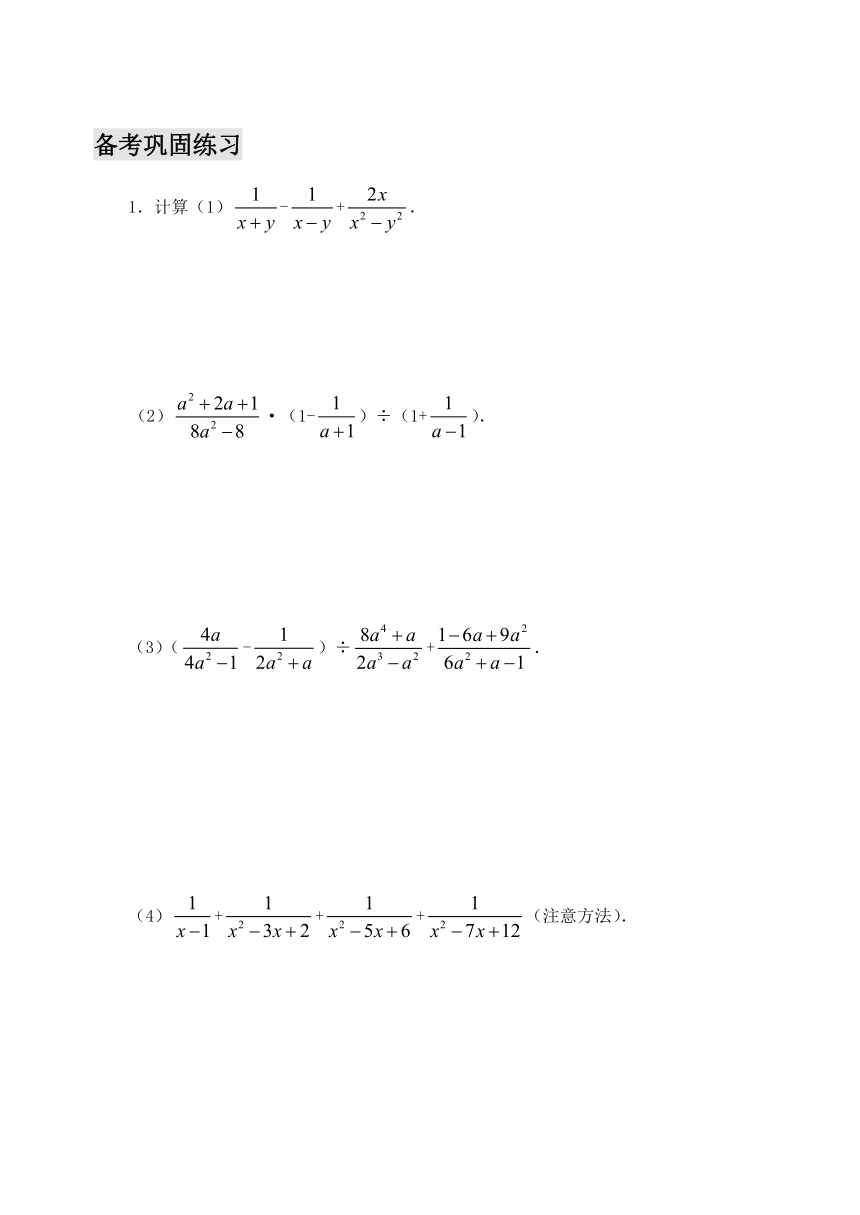
文档简介
第7课 分式的加减
目的:掌握分式的通分、加减运算.毛
中考基础知识
1.通分:将异分母的分式化成______叫做分式的通分.
2.同分母分式相加减:分母_______,分子________,最后还要________.
3.异分母分式相加减:先_______,然后分母________,分子_________,最后仍要________.
4.分式的综合运算注意顺序,尽量用运算律简化运算.
备考例题指导
例1.计算a2-a+1-.
分析:把a2-a+1看做一个整体,看做分母为1的分式,通分后可利用立方和公式计算.
解:原式=-=-==
例2.化简.
分析:用分式基本性质,在分子分母上同乘以x+1比较简便,这是化简繁分式的一般方法.
解:原式===.
例3.错误辨析:有同学这样计算下题,指出他错在哪里,错误原因何在.
计算+-.
解:原式=--
=7(a+2)-12×2-6(a-2)
=7a+14-24-6a+12
=a+2
答:该同学在计算第二步时,去掉了分母,发生了严重错误,原因是他把分式计算与解分式方程混淆了.
注意:分式计算不能去分母,只能通分约分,而解分式方程,才可以去分母.
例4.计算+-.
解:原式=+-(分解分母)
=+-(通分)
=(分母不变,分子相加减)
=(合并分子)
=(分解分子)
=(化简)
例5.已知=,求(2+x)(2+y)+x2的值.
分析:双向化简,整体代换思想体现,数学基本功──式的恒等变形.
解:由已知得(1+x)(1+y)=(1-x)(1-y),
1+x+y+xy=1-x-y+xy,
∴x+y=0.
∴(2+x)(2+y)+x2=4+2(x+y)+xy+x2
=4+xy+x2
=4+x(x+y)=4
备考巩固练习
1.计算(1)-+.
(2)·(1-)÷(1+).
(3)(-)÷+.
(4)+++(注意方法).
2.先化简,再求值(-)÷,其中a满足a2+2a-1=0.
3.先化简,再选取一个使原式有意义,而你又喜欢的数代入求值:-.
4.当a=时,求-的值.
5.(1)计算+-.
(2)解方程+-=0.
6.(2005,绍兴)已知P=-,Q=(x+y)2-2y(x+y),小敏、小聪两人在x=2,y=-1的条件下分别计算了P和Q的值,小敏说P的值比Q大,小聪说Q的值比P大,请你判断谁的结论正确,并说明理由.
答案:
1.(1)原式=-+
===
(2)原式=·÷
=··=
(3)原式=[-]·+
=·+
=+=
(4)原式=+++
=++
=++
=+=
2.原式=[-]·
=·==
当a2+2a-1=0时,原式=1
3.原式=+=x+x-1=2x-1
令x=2,得原式=2×2-1=3
4.原式=-=-2(1+)-(-1)
=-2-2-2+=-4-
5.(1)原式===
(2)方程两边同乘以(x-1)去分母得
x2-2x+1+5x+5-4=0
x2+3x+2=0
x1=-1(舍),x2=-2,∴x=-2是原方程的解.
6.解:P=x+y,Q=x2-y2,当x=2,y=-1时,P=1,Q=3,Q>P,
所以小聪的结论是正确的.毛
目的:掌握分式的通分、加减运算.毛
中考基础知识
1.通分:将异分母的分式化成______叫做分式的通分.
2.同分母分式相加减:分母_______,分子________,最后还要________.
3.异分母分式相加减:先_______,然后分母________,分子_________,最后仍要________.
4.分式的综合运算注意顺序,尽量用运算律简化运算.
备考例题指导
例1.计算a2-a+1-.
分析:把a2-a+1看做一个整体,看做分母为1的分式,通分后可利用立方和公式计算.
解:原式=-=-==
例2.化简.
分析:用分式基本性质,在分子分母上同乘以x+1比较简便,这是化简繁分式的一般方法.
解:原式===.
例3.错误辨析:有同学这样计算下题,指出他错在哪里,错误原因何在.
计算+-.
解:原式=--
=7(a+2)-12×2-6(a-2)
=7a+14-24-6a+12
=a+2
答:该同学在计算第二步时,去掉了分母,发生了严重错误,原因是他把分式计算与解分式方程混淆了.
注意:分式计算不能去分母,只能通分约分,而解分式方程,才可以去分母.
例4.计算+-.
解:原式=+-(分解分母)
=+-(通分)
=(分母不变,分子相加减)
=(合并分子)
=(分解分子)
=(化简)
例5.已知=,求(2+x)(2+y)+x2的值.
分析:双向化简,整体代换思想体现,数学基本功──式的恒等变形.
解:由已知得(1+x)(1+y)=(1-x)(1-y),
1+x+y+xy=1-x-y+xy,
∴x+y=0.
∴(2+x)(2+y)+x2=4+2(x+y)+xy+x2
=4+xy+x2
=4+x(x+y)=4
备考巩固练习
1.计算(1)-+.
(2)·(1-)÷(1+).
(3)(-)÷+.
(4)+++(注意方法).
2.先化简,再求值(-)÷,其中a满足a2+2a-1=0.
3.先化简,再选取一个使原式有意义,而你又喜欢的数代入求值:-.
4.当a=时,求-的值.
5.(1)计算+-.
(2)解方程+-=0.
6.(2005,绍兴)已知P=-,Q=(x+y)2-2y(x+y),小敏、小聪两人在x=2,y=-1的条件下分别计算了P和Q的值,小敏说P的值比Q大,小聪说Q的值比P大,请你判断谁的结论正确,并说明理由.
答案:
1.(1)原式=-+
===
(2)原式=·÷
=··=
(3)原式=[-]·+
=·+
=+=
(4)原式=+++
=++
=++
=+=
2.原式=[-]·
=·==
当a2+2a-1=0时,原式=1
3.原式=+=x+x-1=2x-1
令x=2,得原式=2×2-1=3
4.原式=-=-2(1+)-(-1)
=-2-2-2+=-4-
5.(1)原式===
(2)方程两边同乘以(x-1)去分母得
x2-2x+1+5x+5-4=0
x2+3x+2=0
x1=-1(舍),x2=-2,∴x=-2是原方程的解.
6.解:P=x+y,Q=x2-y2,当x=2,y=-1时,P=1,Q=3,Q>P,
所以小聪的结论是正确的.毛
