第五单元_第09课时_解方程(三)(教学课件)五年级数学上册人教版 (共30张PPT)
文档属性
| 名称 | 第五单元_第09课时_解方程(三)(教学课件)五年级数学上册人教版 (共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-27 12:23:18 | ||
图片预览





文档简介
(共30张PPT)
第08课时 解方程(三)
小学数学·五年级(上)·RJ
目录
01
情境导入—引“探究”
知识链接—构“联系”
02
新知探究—习“方法”
03
05
作业布置---拓“延伸”
达标练习---活“应用”
04
1.能灵活运动等式的性质解方程,进一步熟悉解方程的策略和书写格式。
2.学会解形如ax±b=c和a(x±b)=c类型的方程,提升解方程的能力。
3.在解方程过程中通过由具体到一般的抽象概括过程,培养代数思想和符号意识。
能灵活运动等式的性质解方程,进一步熟悉解方程的策略和书写格式。
学会解形如 ax±b=c和a(x±b)=c 类型的方程,提升解方程的能力。
通过解方程知道解方程的过程实际上是一连串依据等式的性质演绎推理的过程,发展推理意识。
重 点
核心素养
难 点
课前引入
总结:解方程的一般步骤。
1.解下列方程,并说一说依据是什么?
2.5x=20
解:2.5x÷2.5=20÷2.5
x=8
36-x=12
解:36-x+x=12+x
36=12+x
12+x=36
x=24
2.回顾等式的性质。
等式两边加上或减去同一个数,左右两边仍然相等。
等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
等式的性质
性质1:
性质2:
能灵活运动等式的性质解方程,学会解形如 ax±b=c类型的方程。
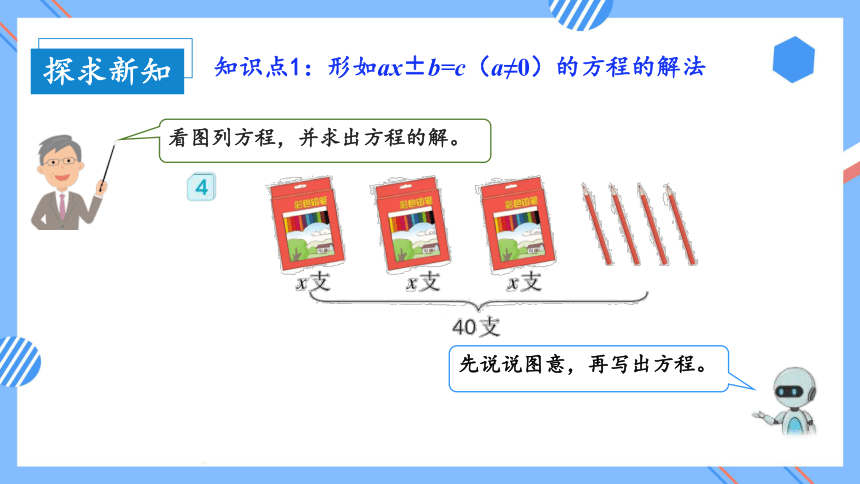
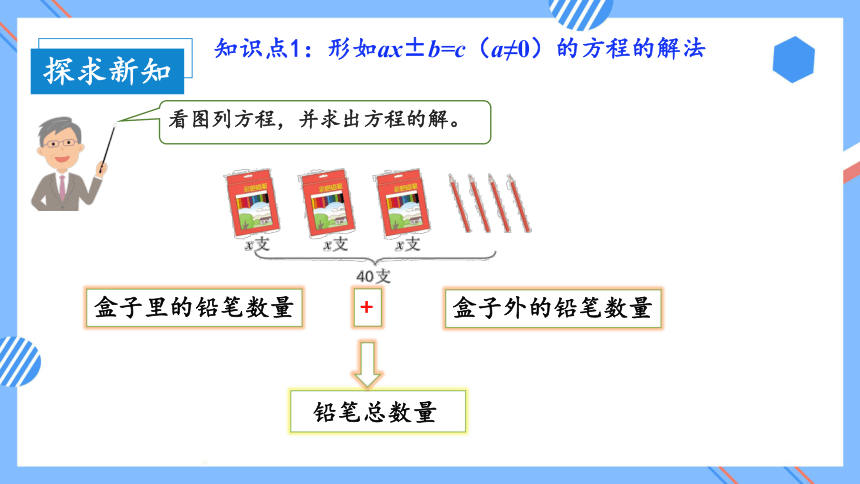
看图列方程,并求出方程的解。
先说说图意,再写出方程。
知识点1:形如ax±b=c(a≠0)的方程的解法
看图列方程,并求出方程的解。
知识点1:形如ax±b=c(a≠0)的方程的解法
+
铅笔总数量
盒子外的铅笔数量
盒子里的铅笔数量
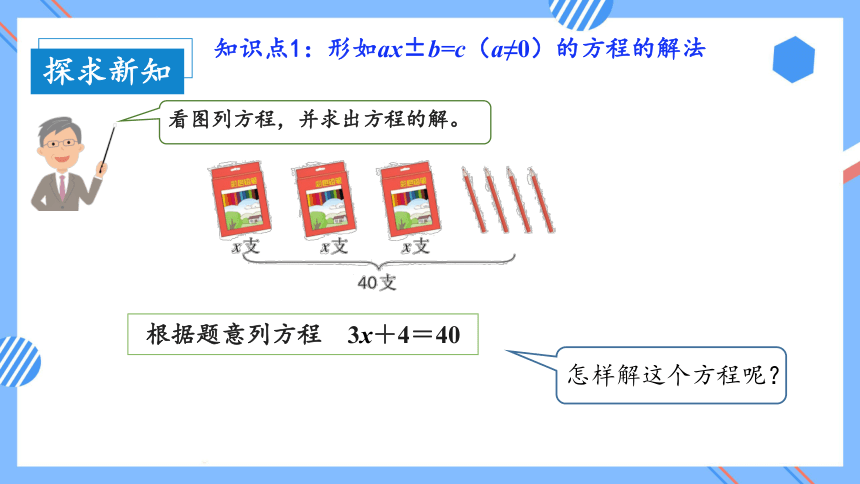
看图列方程,并求出方程的解。
知识点1:形如ax±b=c(a≠0)的方程的解法
根据题意列方程 3x+4=40
怎样解这个方程呢?
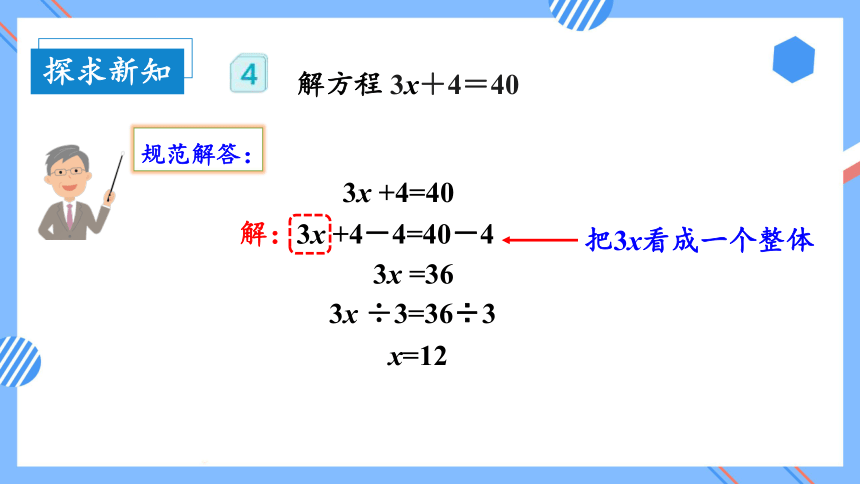
解方程 3x+4=40
规范解答:
3x +4=40
解:3x +4-4=40-4
3x =36
3x ÷3=36÷3
x=12
把3x看成一个整体
解方程 3x+4=40
说一说解方程的思路。
3x +4=40
解:3x +4-4=40-4
3x =36
3x ÷3=36÷3
x=12
我们把“3x”看成一个整体,根据等式的基本性质1,两边同时减去4,先求出3x的值。再根据等式的基本性质2,两边同时除以3,求出x的值。
别忘了检验!
解方程 3x+4=40
3x +4=40
解:3x +4-4=40-4
3x =36
3x ÷3=36÷3
x=12
把x=12代入方程,
方程左边=3x+4
=3×12+4
=36+4
=40
=方程右边
所以,x=12是方程的解。
解形如ax ±b=c(a≠0)的方程时,可以把 ax 看成一个整体,先求出这个整体是多少,再求出x的值。
能灵活运动等式的性质解方程,学会解形如ax±b=c类型的方程。
解方程 2(x-16)=8
乘法分配律
2(x - 16)=8
解:2x-32=8
2x-32+32=8+32
2x=40
2x÷2=40÷2
x=20
x - 16=4
x =20
2(x - 16)=8
把(x-16)看成一个整体
把2x看成一个整体
解:2(x - 16)÷2=8÷2
这两种方法,分别是把哪个式子看成一个整体?
知识点2:形如a(x±b)=c(a≠0)的方程的解法
2(x - 16)=8
解:2x-32=8
2x-32+32=8+32
2x=40
2x÷2=40÷2
x -16+16=4+16
解:2(x - 16)÷2=8÷2
x - 16=4
x =20
2(x - 16)=8
x=20
把(x-16)看成一个整体,根据等式的基本性质2,两边先同时除以2,得到x-16=4,然后根据等式的基本性质1,两边同时加16,最后求出x=20。
说说解题的思路:
知识点2:形如a(x±b)=c(a≠0)的方程的解法
2(x - 16)=8
解:2x-32=8
2x-32+32=8+32
2x=40
2x÷2=40÷2
x -16+16=4+16
解:2(x - 16)÷2=8÷2
x - 16=4
x =20
2(x - 16)=8
x=20
我是先利用乘法分配律,整理方程2x-32=8,把2x看成一个整体,再根据等式的基本性质1,两边同时加32求出2x=40,最后根据等式的基本性质2,两边同时除以2求出x=20。
说说解题的思路:
知识点2:形如a(x±b)=c(a≠0)的方程的解法
2(x - 16)=8
解:2x-32=8
2x-32+32=8+32
2x=40
2x÷2=40÷2
x=20
方程左边=2×(20-16)
=2×4
=8
=方程右边
所以,x=20是方程的解。
把x=20代入方程去检验
别忘了检验哦!
拓展延伸
3x +4=40
x +3=9
2(x - 16)=8
3x =18
转化
相同的是都要根据等式的基本性质来解方程。
今天学习的方程与前面的方程有什么区别和联系?
解复杂方程前,最关键是看清把什么看成一个整体,转化为已学的方程。
通过分层练习,进一步巩固利用等式的性质解方程的方法。
课堂练习
1.看图列方程,并求出方程的解。
x元/本
1.5元
7.5元
5x +1.5=7.5
解:5x +1.5-1.5=7.5-1.5
5x =6
5x÷5 =6÷5
x =1.2
把5x看成一个整体
课堂练习
2.解下列方程。
6x-35=13
3x-12×6=6
解: 3x-72=6
3x-72+72=6+72
3x=78
x=26
解:6x-35+35=13+35
6x=48
6x÷6=48 ÷6
x=8
课堂练习
2.解下列方程。
(5x-12)×8=24
(100-3x)÷2=8
解:(5x-12)×8÷8=24÷8
5x-12=3
5x-12+12=3+12
5x=15
x=3
解:(100-3x)÷2×2=8×2
100-3x=16
100-3x+ 3x=16+ 3x
100= 16+ 3x
16+ 3x= 100
16+ 3x-16= 100-16
3x=84
3x÷3=84÷3
x=28
学以致用
3.看图列方程,并求出方程的解。
30 30 x x
158
30×2+2x=158
解: 60+2x=158
60+2x-60=158-60
2x=98
2x÷2=98÷2
x=49
学以致用
4.把下面每个方程和它的解连起来。
x+13=33
x=0
7(x-20)=140
x=10
1.8x=54
x=20
6.7x-60.3=6.7
x=30
9x+x=0
x=40
拓展练习
5. 看图列方程,并求出方程的解。
(x+5)×2=36
解: 2x+10-10=36-10
2x÷2=26÷2
x=13
拓展练习
5. 看图列方程,并求出方程的解。
x+3x=80
解: 4x=80
4x÷4=80÷4
x=20
成人:
儿童:
共80人
x 人
x 人
x 人
x 人
拓展练习
6.*在 里填上适当的数,使每个方程的解都是x=5。
+x=13
x- =2.3
×x=7
x÷ =50
8
2.7
1.4
0.1
这节课你有什么收获?
归纳总结:
简单方程
多次利用等式的基本性质解方程。
复杂方程
看清把什么看成一个整体。
利用一次等式的基本性质解方程。
第08课时 解方程(三)
小学数学·五年级(上)·RJ
目录
01
情境导入—引“探究”
知识链接—构“联系”
02
新知探究—习“方法”
03
05
作业布置---拓“延伸”
达标练习---活“应用”
04
1.能灵活运动等式的性质解方程,进一步熟悉解方程的策略和书写格式。
2.学会解形如ax±b=c和a(x±b)=c类型的方程,提升解方程的能力。
3.在解方程过程中通过由具体到一般的抽象概括过程,培养代数思想和符号意识。
能灵活运动等式的性质解方程,进一步熟悉解方程的策略和书写格式。
学会解形如 ax±b=c和a(x±b)=c 类型的方程,提升解方程的能力。
通过解方程知道解方程的过程实际上是一连串依据等式的性质演绎推理的过程,发展推理意识。
重 点
核心素养
难 点
课前引入
总结:解方程的一般步骤。
1.解下列方程,并说一说依据是什么?
2.5x=20
解:2.5x÷2.5=20÷2.5
x=8
36-x=12
解:36-x+x=12+x
36=12+x
12+x=36
x=24
2.回顾等式的性质。
等式两边加上或减去同一个数,左右两边仍然相等。
等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
等式的性质
性质1:
性质2:
能灵活运动等式的性质解方程,学会解形如 ax±b=c类型的方程。
看图列方程,并求出方程的解。
先说说图意,再写出方程。
知识点1:形如ax±b=c(a≠0)的方程的解法
看图列方程,并求出方程的解。
知识点1:形如ax±b=c(a≠0)的方程的解法
+
铅笔总数量
盒子外的铅笔数量
盒子里的铅笔数量
看图列方程,并求出方程的解。
知识点1:形如ax±b=c(a≠0)的方程的解法
根据题意列方程 3x+4=40
怎样解这个方程呢?
解方程 3x+4=40
规范解答:
3x +4=40
解:3x +4-4=40-4
3x =36
3x ÷3=36÷3
x=12
把3x看成一个整体
解方程 3x+4=40
说一说解方程的思路。
3x +4=40
解:3x +4-4=40-4
3x =36
3x ÷3=36÷3
x=12
我们把“3x”看成一个整体,根据等式的基本性质1,两边同时减去4,先求出3x的值。再根据等式的基本性质2,两边同时除以3,求出x的值。
别忘了检验!
解方程 3x+4=40
3x +4=40
解:3x +4-4=40-4
3x =36
3x ÷3=36÷3
x=12
把x=12代入方程,
方程左边=3x+4
=3×12+4
=36+4
=40
=方程右边
所以,x=12是方程的解。
解形如ax ±b=c(a≠0)的方程时,可以把 ax 看成一个整体,先求出这个整体是多少,再求出x的值。
能灵活运动等式的性质解方程,学会解形如ax±b=c类型的方程。
解方程 2(x-16)=8
乘法分配律
2(x - 16)=8
解:2x-32=8
2x-32+32=8+32
2x=40
2x÷2=40÷2
x=20
x - 16=4
x =20
2(x - 16)=8
把(x-16)看成一个整体
把2x看成一个整体
解:2(x - 16)÷2=8÷2
这两种方法,分别是把哪个式子看成一个整体?
知识点2:形如a(x±b)=c(a≠0)的方程的解法
2(x - 16)=8
解:2x-32=8
2x-32+32=8+32
2x=40
2x÷2=40÷2
x -16+16=4+16
解:2(x - 16)÷2=8÷2
x - 16=4
x =20
2(x - 16)=8
x=20
把(x-16)看成一个整体,根据等式的基本性质2,两边先同时除以2,得到x-16=4,然后根据等式的基本性质1,两边同时加16,最后求出x=20。
说说解题的思路:
知识点2:形如a(x±b)=c(a≠0)的方程的解法
2(x - 16)=8
解:2x-32=8
2x-32+32=8+32
2x=40
2x÷2=40÷2
x -16+16=4+16
解:2(x - 16)÷2=8÷2
x - 16=4
x =20
2(x - 16)=8
x=20
我是先利用乘法分配律,整理方程2x-32=8,把2x看成一个整体,再根据等式的基本性质1,两边同时加32求出2x=40,最后根据等式的基本性质2,两边同时除以2求出x=20。
说说解题的思路:
知识点2:形如a(x±b)=c(a≠0)的方程的解法
2(x - 16)=8
解:2x-32=8
2x-32+32=8+32
2x=40
2x÷2=40÷2
x=20
方程左边=2×(20-16)
=2×4
=8
=方程右边
所以,x=20是方程的解。
把x=20代入方程去检验
别忘了检验哦!
拓展延伸
3x +4=40
x +3=9
2(x - 16)=8
3x =18
转化
相同的是都要根据等式的基本性质来解方程。
今天学习的方程与前面的方程有什么区别和联系?
解复杂方程前,最关键是看清把什么看成一个整体,转化为已学的方程。
通过分层练习,进一步巩固利用等式的性质解方程的方法。
课堂练习
1.看图列方程,并求出方程的解。
x元/本
1.5元
7.5元
5x +1.5=7.5
解:5x +1.5-1.5=7.5-1.5
5x =6
5x÷5 =6÷5
x =1.2
把5x看成一个整体
课堂练习
2.解下列方程。
6x-35=13
3x-12×6=6
解: 3x-72=6
3x-72+72=6+72
3x=78
x=26
解:6x-35+35=13+35
6x=48
6x÷6=48 ÷6
x=8
课堂练习
2.解下列方程。
(5x-12)×8=24
(100-3x)÷2=8
解:(5x-12)×8÷8=24÷8
5x-12=3
5x-12+12=3+12
5x=15
x=3
解:(100-3x)÷2×2=8×2
100-3x=16
100-3x+ 3x=16+ 3x
100= 16+ 3x
16+ 3x= 100
16+ 3x-16= 100-16
3x=84
3x÷3=84÷3
x=28
学以致用
3.看图列方程,并求出方程的解。
30 30 x x
158
30×2+2x=158
解: 60+2x=158
60+2x-60=158-60
2x=98
2x÷2=98÷2
x=49
学以致用
4.把下面每个方程和它的解连起来。
x+13=33
x=0
7(x-20)=140
x=10
1.8x=54
x=20
6.7x-60.3=6.7
x=30
9x+x=0
x=40
拓展练习
5. 看图列方程,并求出方程的解。
(x+5)×2=36
解: 2x+10-10=36-10
2x÷2=26÷2
x=13
拓展练习
5. 看图列方程,并求出方程的解。
x+3x=80
解: 4x=80
4x÷4=80÷4
x=20
成人:
儿童:
共80人
x 人
x 人
x 人
x 人
拓展练习
6.*在 里填上适当的数,使每个方程的解都是x=5。
+x=13
x- =2.3
×x=7
x÷ =50
8
2.7
1.4
0.1
这节课你有什么收获?
归纳总结:
简单方程
多次利用等式的基本性质解方程。
复杂方程
看清把什么看成一个整体。
利用一次等式的基本性质解方程。
