物理人教版(2019)选择性必修第一册1.5 弹性碰撞和非弹性碰撞 (16张PPT)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册1.5 弹性碰撞和非弹性碰撞 (16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-10-27 10:33:26 | ||
图片预览






文档简介
(共16张PPT)
1.5 弹性碰撞和非弹性碰撞
学习目标
1、了解弹性碰撞和非弹性碰撞。
2、会分析具体实例中的碰撞特点及类型。
3、知道对心碰撞和非对心碰撞,加深对动量守恒定律和机械能守恒定律的理解。
1、碰撞过程的特点
(1)相互作用时间极短。
(2)相互作用力极大,即内力远大于外力,动量守恒
(3)可以认为物体在碰撞前、后仍在同一位置。
(1)对心碰撞和非对心碰撞(一维碰撞和二维碰撞)
2、碰撞的分类
①对心碰撞:碰撞前后速度都沿同一条直线
②非对心碰撞:碰撞前后速度不沿同一条直线
物体碰撞过程中系统动量守恒。那么,在各种碰撞中能量又是如何变化的?
一、碰撞
为什么碰撞过程中出现了能量损失呢?
要看碰撞后形变能否恢复
(多选)如图,在光滑水平面上的A、B两个小球发生正碰,两小球质量分别为m1和m2,图乙为它们碰撞前后的x-t图像,m1=0.1kg。由此判断( )
A.碰前B静止,A向右运动
B.碰后B和A都向右运动
C.由动量守恒可以算出m2=0.3 kg
D.碰撞过程中系统损失了0.4J的机械能
E.此碰撞属于非弹性碰撞
1、弹性碰撞:系统在碰撞前后动能保持不变。(系统的动能减少为0)
(2)碰撞碰撞和非弹性碰撞
2、非弹性碰撞:系统在碰撞后动能减少。
3、完全非弹性碰撞:碰撞后两个物体结为一体(系统的动能减少最多)(是非弹性碰撞的特殊情况)
AC
练习、(2022·新疆·乌鲁木齐高二期中)如图,A,B两小球质量相同,在光滑水平面上分别以动量p1=8kg.m/s 和p2=6kg.m/s(向右为参考系正方向)做匀速直线运动,则在A球追上B球并与之碰撞的过程中,两小球碰撞后的动量p1/和p2/可能分别为( )
A.5kg.m/s , 9kg.m/s
B.10kg.m/s ,4kg.m/s
C.7kg.m/s, 7kg.m/s
D.2kg.m/s , 12kg.m/s
1.动量守恒:p1+p2=p1′+p2′.
2.动能不增加:Ek1+Ek2≥Ek1′+Ek2′
3.速度要符合情景:
b.碰前两物体相向运动,碰后两物体的运动方向不可能都不改变。
归纳:合理碰撞三原则(碰撞的可能性判断)
C
a. 同向运动追上相碰:
且
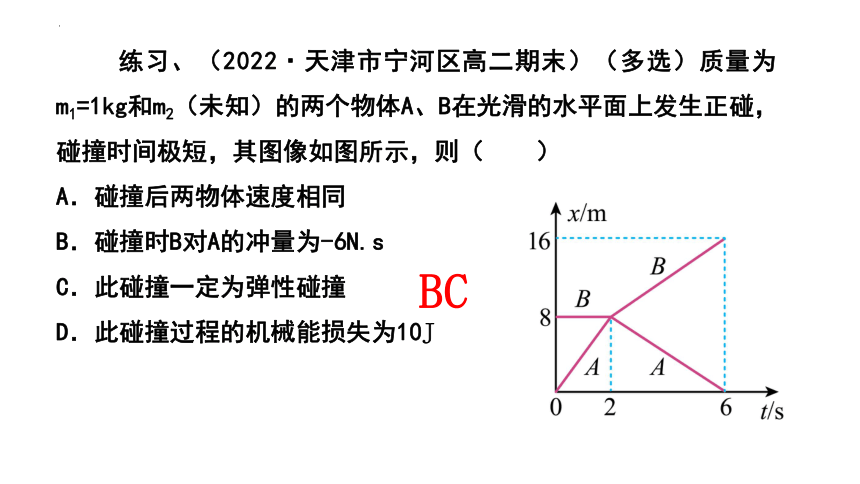
练习、(2022·天津市宁河区高二期末)(多选)质量为m1=1kg和m2(未知)的两个物体A、B在光滑的水平面上发生正碰,碰撞时间极短,其图像如图所示,则( )
A.碰撞后两物体速度相同
B.碰撞时B对A的冲量为-6N.s
C.此碰撞一定为弹性碰撞
D.此碰撞过程的机械能损失为10J
BC
练习、(2022·内蒙古·高三练习)对于两个质量相同的物体发生速度在同一直线上的弹性碰撞过程,可以简化为如下模型:在光滑水平面上,物体A的左边固定有轻质弹簧,与A质量相同的物体B以速度v向A运动并与弹簧发生碰撞,A、B始终沿同一直线运动。设物体的质量均为m=2kg,开始时A静止在光滑水平面上某点,B以速度v0=2.0m/s从远处沿该直线向A运动,如图所示,A、B组成的系统动能损失的最大值为( )
A.1J B.2J C.3J D.4J
B
弹性势能的最大值为( )
B
二、弹性碰撞的实例:(动碰静)
情境:假设物体m1以速度v1与原来静止的物体m2发生弹性正碰,如图所示。碰撞后它们的速度分别为v1′和v2′。
动量守恒:
解得:
弹性碰撞
机械能守恒:
此式证明动量守恒
此式证明是弹性碰撞
结论:(弹性碰撞)
(1)当m1=m2时,v1′=0,v2′=v1(质量相等,速度交换)
(2)当m1>m2时,v1′>0,v2′>0,且v2′>v1′(大碰小,一起跑)
(3)当m1<m2时,v1′<0,v2′>0(小碰大,要反弹)
(4)当m1 m2时,v1′=v0,v2′=2v1(极大碰极小,大不变,小加倍)
(5)当m1 m2时,v1′=-v1,v2′=0(极小碰极大,小等速率反弹,大不变)
练习、(2022·四川·凉山高二阶段练习)如图所示,B、C、D、E、F,5个小球并排放置在光滑的水平面上,B、C、D、E,4个球质量相等,而F球质量小于B球质量,A球的质量等于 F球质量。A球以速度v0向B球运动,所发生的碰撞均为弹性碰撞,则碰撞之后( )
A.5个小球静止,1个小球运动
B.4个小球静止,2个小球运动
C.3个小球静止,3个小球运动
D.6个小球都运动
C
练习、小球1追碰小球2,碰撞前两球的动量分别为P1=5kgm/s,P2=5kgm/s,发生正碰后小球2的动量P2/=10kgm/s,则两球的质量关系可能为( )
A.m2 = m1
B.m2 = 2m1
C.m2 = 4m1
D.m2 = 6m1
C
练习、(2022·云南·玉溪高三练习)用轻弹簧相连的质量均为2kg的A、B两物块都以的速度在光滑的水平地面上运动,弹簧处于原长,质量为4kg的物体C静止在前方,如图所示,B与C碰撞后二者粘在一起运动。在以后的运动中,求:
(1)当弹簧的弹性势能最大时物体A的速度多大?
(2)弹性势能的最大值是多大?
(1)三者第一次共速时,弹簧的压缩量最大,弹性势能最大,据动量守恒定律可得 ,解v共=3m/s,弹性势能最大时物A速度大小为3m/s
(2)设B、C粘在一起后共同速度为,据动量守恒定律可得
,解得vB=2m/s,
据机械能守恒定律可得,最大弹性势能为
代入数据解得Ep=12J。
(1)3m/s;(2)12J
碰撞过程中系统动量守恒:
弹性碰撞中没有机械能损失:
情境:若在一光滑水平面上有两个质量分别为m1、m2的刚性小球A和B,以初速度v1、v2运动,若它们能发生碰撞(为一维弹性碰撞),碰撞后它们的速度分别为v’1和v’2分别是多大?
拓展延伸——动碰动的弹性碰撞:
解得:
1. 弹性碰撞:碰撞过程中机械能守恒,这样的碰撞叫做弹性碰撞。
(1) 规律:动量守恒、机械能守恒
(2) 能量转化情况:系统动能没有损失
2. 非弹性碰撞:碰撞过程中机械能不守恒,这样的碰撞叫做非弹性碰撞。
(1) 规律:动量守恒,机械能减少
(2) 能量转化情况:完全非弹性碰撞中系统动能损失最大
3. 对心碰撞和非对心碰撞
课堂总结
练习、(2021·云南·高三期中)(多选)如图所示,在光滑水平面上,静止着一个质量为m1的小球A,另一相同大小、质量为m2的小球B,以速度v与A发生弹性正碰,若碰后A、B两球的速度大小之比为3:1,则两球质量关系正确的是( )
A.2m1= m2
B.3m1= 5m2
C.5m1= 3m2
D.3m1= m2
BD
练习、(2021·湖北高二阶段练习)如图,质量为m的A球以速度v0在光滑水平面上运动,与原来静止的质量为4m的B球碰撞,碰撞后A球以v=av0 (待定系数a<1)的速率弹回,并与挡板P发生完全弹性碰撞,若要使A球能追上B球再次相撞,则a的取值范围为( )
A. B.
C. D.
D
详解:设碰后B球的速度大小为v1,据动量守恒定律有 ①,根据碰撞过程中机械能不会增加,有 ②,A球与挡板P发生完全弹性碰撞后速度大小不变,则若要使A球能追上B球再次相撞,应有 ③,联立①②③解得a的取值范围为 ,故选D。
1.5 弹性碰撞和非弹性碰撞
学习目标
1、了解弹性碰撞和非弹性碰撞。
2、会分析具体实例中的碰撞特点及类型。
3、知道对心碰撞和非对心碰撞,加深对动量守恒定律和机械能守恒定律的理解。
1、碰撞过程的特点
(1)相互作用时间极短。
(2)相互作用力极大,即内力远大于外力,动量守恒
(3)可以认为物体在碰撞前、后仍在同一位置。
(1)对心碰撞和非对心碰撞(一维碰撞和二维碰撞)
2、碰撞的分类
①对心碰撞:碰撞前后速度都沿同一条直线
②非对心碰撞:碰撞前后速度不沿同一条直线
物体碰撞过程中系统动量守恒。那么,在各种碰撞中能量又是如何变化的?
一、碰撞
为什么碰撞过程中出现了能量损失呢?
要看碰撞后形变能否恢复
(多选)如图,在光滑水平面上的A、B两个小球发生正碰,两小球质量分别为m1和m2,图乙为它们碰撞前后的x-t图像,m1=0.1kg。由此判断( )
A.碰前B静止,A向右运动
B.碰后B和A都向右运动
C.由动量守恒可以算出m2=0.3 kg
D.碰撞过程中系统损失了0.4J的机械能
E.此碰撞属于非弹性碰撞
1、弹性碰撞:系统在碰撞前后动能保持不变。(系统的动能减少为0)
(2)碰撞碰撞和非弹性碰撞
2、非弹性碰撞:系统在碰撞后动能减少。
3、完全非弹性碰撞:碰撞后两个物体结为一体(系统的动能减少最多)(是非弹性碰撞的特殊情况)
AC
练习、(2022·新疆·乌鲁木齐高二期中)如图,A,B两小球质量相同,在光滑水平面上分别以动量p1=8kg.m/s 和p2=6kg.m/s(向右为参考系正方向)做匀速直线运动,则在A球追上B球并与之碰撞的过程中,两小球碰撞后的动量p1/和p2/可能分别为( )
A.5kg.m/s , 9kg.m/s
B.10kg.m/s ,4kg.m/s
C.7kg.m/s, 7kg.m/s
D.2kg.m/s , 12kg.m/s
1.动量守恒:p1+p2=p1′+p2′.
2.动能不增加:Ek1+Ek2≥Ek1′+Ek2′
3.速度要符合情景:
b.碰前两物体相向运动,碰后两物体的运动方向不可能都不改变。
归纳:合理碰撞三原则(碰撞的可能性判断)
C
a. 同向运动追上相碰:
且
练习、(2022·天津市宁河区高二期末)(多选)质量为m1=1kg和m2(未知)的两个物体A、B在光滑的水平面上发生正碰,碰撞时间极短,其图像如图所示,则( )
A.碰撞后两物体速度相同
B.碰撞时B对A的冲量为-6N.s
C.此碰撞一定为弹性碰撞
D.此碰撞过程的机械能损失为10J
BC
练习、(2022·内蒙古·高三练习)对于两个质量相同的物体发生速度在同一直线上的弹性碰撞过程,可以简化为如下模型:在光滑水平面上,物体A的左边固定有轻质弹簧,与A质量相同的物体B以速度v向A运动并与弹簧发生碰撞,A、B始终沿同一直线运动。设物体的质量均为m=2kg,开始时A静止在光滑水平面上某点,B以速度v0=2.0m/s从远处沿该直线向A运动,如图所示,A、B组成的系统动能损失的最大值为( )
A.1J B.2J C.3J D.4J
B
弹性势能的最大值为( )
B
二、弹性碰撞的实例:(动碰静)
情境:假设物体m1以速度v1与原来静止的物体m2发生弹性正碰,如图所示。碰撞后它们的速度分别为v1′和v2′。
动量守恒:
解得:
弹性碰撞
机械能守恒:
此式证明动量守恒
此式证明是弹性碰撞
结论:(弹性碰撞)
(1)当m1=m2时,v1′=0,v2′=v1(质量相等,速度交换)
(2)当m1>m2时,v1′>0,v2′>0,且v2′>v1′(大碰小,一起跑)
(3)当m1<m2时,v1′<0,v2′>0(小碰大,要反弹)
(4)当m1 m2时,v1′=v0,v2′=2v1(极大碰极小,大不变,小加倍)
(5)当m1 m2时,v1′=-v1,v2′=0(极小碰极大,小等速率反弹,大不变)
练习、(2022·四川·凉山高二阶段练习)如图所示,B、C、D、E、F,5个小球并排放置在光滑的水平面上,B、C、D、E,4个球质量相等,而F球质量小于B球质量,A球的质量等于 F球质量。A球以速度v0向B球运动,所发生的碰撞均为弹性碰撞,则碰撞之后( )
A.5个小球静止,1个小球运动
B.4个小球静止,2个小球运动
C.3个小球静止,3个小球运动
D.6个小球都运动
C
练习、小球1追碰小球2,碰撞前两球的动量分别为P1=5kgm/s,P2=5kgm/s,发生正碰后小球2的动量P2/=10kgm/s,则两球的质量关系可能为( )
A.m2 = m1
B.m2 = 2m1
C.m2 = 4m1
D.m2 = 6m1
C
练习、(2022·云南·玉溪高三练习)用轻弹簧相连的质量均为2kg的A、B两物块都以的速度在光滑的水平地面上运动,弹簧处于原长,质量为4kg的物体C静止在前方,如图所示,B与C碰撞后二者粘在一起运动。在以后的运动中,求:
(1)当弹簧的弹性势能最大时物体A的速度多大?
(2)弹性势能的最大值是多大?
(1)三者第一次共速时,弹簧的压缩量最大,弹性势能最大,据动量守恒定律可得 ,解v共=3m/s,弹性势能最大时物A速度大小为3m/s
(2)设B、C粘在一起后共同速度为,据动量守恒定律可得
,解得vB=2m/s,
据机械能守恒定律可得,最大弹性势能为
代入数据解得Ep=12J。
(1)3m/s;(2)12J
碰撞过程中系统动量守恒:
弹性碰撞中没有机械能损失:
情境:若在一光滑水平面上有两个质量分别为m1、m2的刚性小球A和B,以初速度v1、v2运动,若它们能发生碰撞(为一维弹性碰撞),碰撞后它们的速度分别为v’1和v’2分别是多大?
拓展延伸——动碰动的弹性碰撞:
解得:
1. 弹性碰撞:碰撞过程中机械能守恒,这样的碰撞叫做弹性碰撞。
(1) 规律:动量守恒、机械能守恒
(2) 能量转化情况:系统动能没有损失
2. 非弹性碰撞:碰撞过程中机械能不守恒,这样的碰撞叫做非弹性碰撞。
(1) 规律:动量守恒,机械能减少
(2) 能量转化情况:完全非弹性碰撞中系统动能损失最大
3. 对心碰撞和非对心碰撞
课堂总结
练习、(2021·云南·高三期中)(多选)如图所示,在光滑水平面上,静止着一个质量为m1的小球A,另一相同大小、质量为m2的小球B,以速度v与A发生弹性正碰,若碰后A、B两球的速度大小之比为3:1,则两球质量关系正确的是( )
A.2m1= m2
B.3m1= 5m2
C.5m1= 3m2
D.3m1= m2
BD
练习、(2021·湖北高二阶段练习)如图,质量为m的A球以速度v0在光滑水平面上运动,与原来静止的质量为4m的B球碰撞,碰撞后A球以v=av0 (待定系数a<1)的速率弹回,并与挡板P发生完全弹性碰撞,若要使A球能追上B球再次相撞,则a的取值范围为( )
A. B.
C. D.
D
详解:设碰后B球的速度大小为v1,据动量守恒定律有 ①,根据碰撞过程中机械能不会增加,有 ②,A球与挡板P发生完全弹性碰撞后速度大小不变,则若要使A球能追上B球再次相撞,应有 ③,联立①②③解得a的取值范围为 ,故选D。
