人教版必修二8.1 基本立体图形 课件(32张PPT)
文档属性
| 名称 | 人教版必修二8.1 基本立体图形 课件(32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-27 08:30:42 | ||
图片预览





文档简介
(共32张PPT)
8.1 基本立体图形--多面体
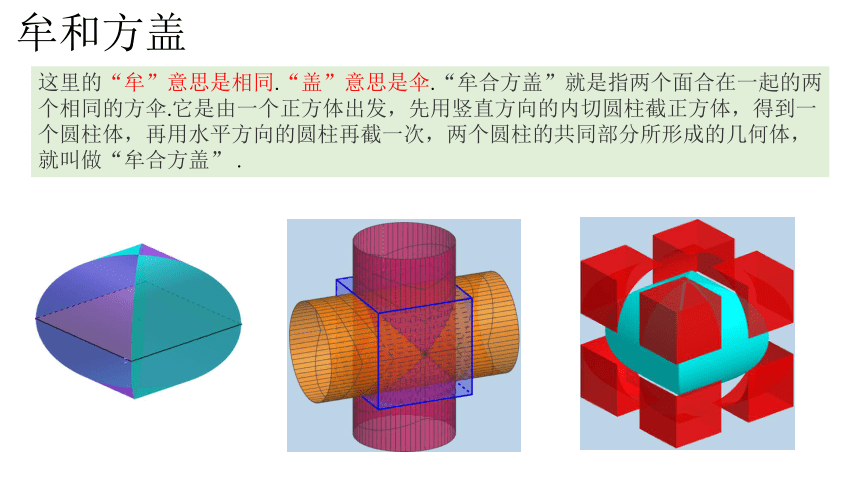
牟和方盖
这里的“牟”意思是相同.“盖”意思是伞.“牟合方盖”就是指两个面合在一起的两个相同的方伞.它是由一个正方体出发,先用竖直方向的内切圆柱截正方体,得到一个圆柱体,再用水平方向的圆柱再截一次,两个圆柱的共同部分所形成的几何体,就叫做“牟合方盖” .
我们生活的空间是三维空间,触摸到的物体几乎都和几何体有关,在小学、初中我们接触过一些特殊的几何体:正方体、圆柱体、球等。在生活中,我们也常见到一些建筑物,它们实际上是由几种空间几何体组合在一起形成的,今天我们一起来研究其中一些基本的空间几何体.
空间几何体:
对于空间的物体,如果只考虑它的的形状、大小和位置,而不考虑物体的其他因素,从中抽象出来的空间图形叫做空间几何体
比较图中物体,围成它们的面有什么不同?如何分类?
(7)
(8)
(5)
(4)
(3)
(2)
(6)
(1)
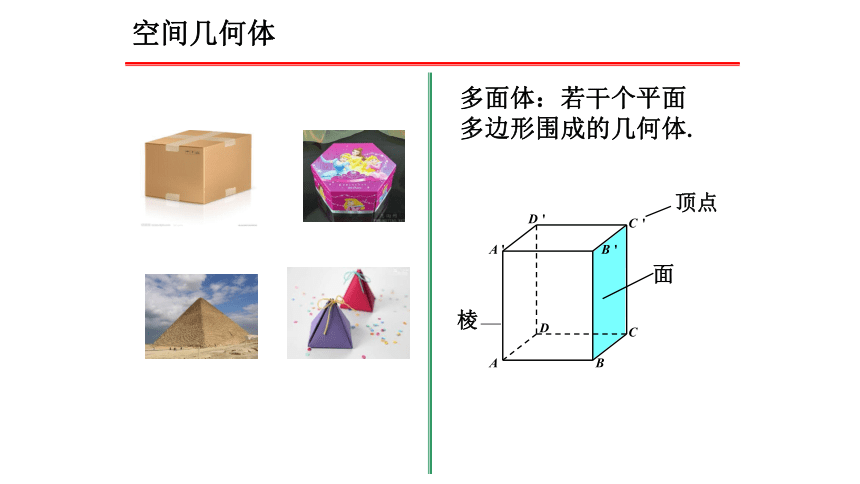
空间几何体
多面体:若干个平面多边形围成的几何体.
空间几何体
面
棱
顶点
轴
空间几何体
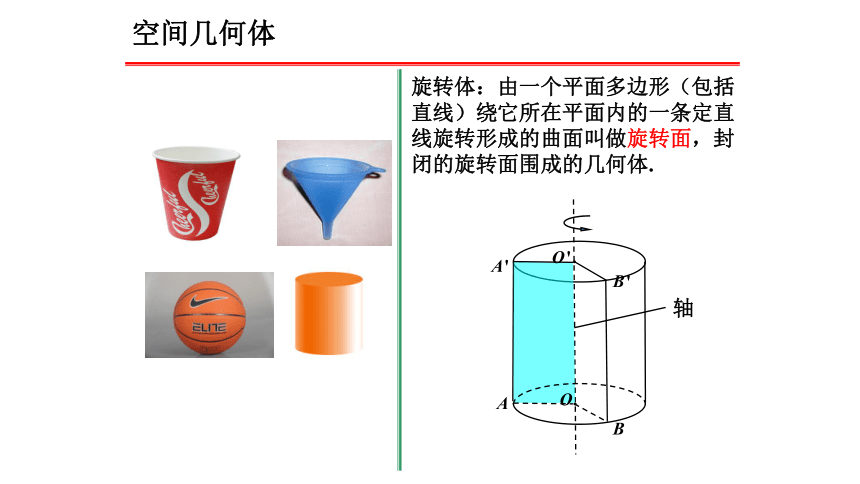
旋转体:由一个平面多边形(包括直线)绕它所在平面内的一条定直线旋转形成的曲面叫做旋转面,封闭的旋转面围成的几何体.
空间几何体的分类:
1.多面体:由若干平面多边形围成的几何体
2.旋转体:由一个平面图形绕它所在的平面内的一条定直线旋转所成的封闭几何体
空间几何体的定义:
如果只考虑物体的形状和大小,而不考虑其它因素,那么这些由物体抽象出来的空间图形就叫做空间几何体
归纳小结
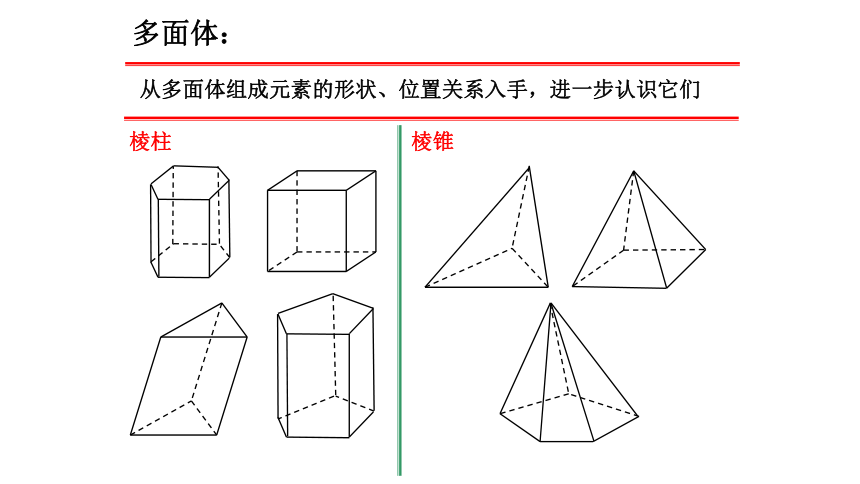
从多面体组成元素的形状、位置关系入手,进一步认识它们
多面体:
棱柱
棱锥
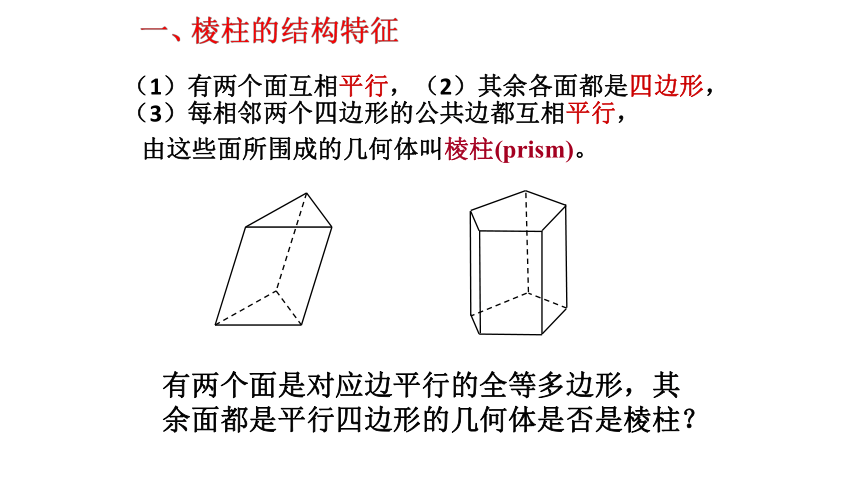
(1)有两个面互相平行,(2)其余各面都是四边形,(3)每相邻两个四边形的公共边都互相平行,
由这些面所围成的几何体叫棱柱(prism)。
有两个面是对应边平行的全等多边形,其余面都是平行四边形的几何体是否是棱柱?
在数学史上,对棱柱的定义也走过一些弯路,如:《几何原本》中定义一个棱柱是一个立体图形,它是由一些平面构成的,其中有两个面是相对的、相等的、相似且平行的,其他各个面都是平行四边形。
波利亚棱柱反例
有两个面是对应边平行的全等多边形,其余面都是平行四边形的几何体是否是棱柱?
底面
侧面
侧棱
顶点
六棱柱:
棱柱的底面互相平行且相等
棱柱的侧面都是平行四边形
棱柱的侧棱都是平行且相等
棱柱的分类:棱柱的底面可以是三角形、四边形、五边形、 …… 我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……
三棱柱
四棱柱
五棱柱
棱柱的分类二:(根据侧棱与底面的关系):
斜棱柱: 侧棱不垂直于底面的棱柱.
直棱柱: 侧棱垂直于底面的棱柱叫做直棱柱
棱柱概念的推广
(1)斜棱柱:侧棱不垂直于底面的棱柱叫做斜棱柱.
(2)直棱柱:侧棱垂直于底面的棱柱叫做直棱柱.
(3)正棱柱:底面是正多边形的直棱柱叫做正棱柱.
(4)平行六面体:底面是平行四边形的四棱柱叫做平行六面体,即平行六面体的六个面都是平行四边形.
(5)长方体:底面是矩形的直棱柱叫做长方体.
(6)正方体:棱长都相等的长方体叫做正方体.
四棱柱的分类
A
B
F
E
G
C
四棱柱
平行六面体
直平行六面体
长方体
正四棱柱
正方体
D
(1) 一个面是多边形
(2) 其余各面都是有一个公共顶点的三角形,
由这些面围成的的多面体叫做棱锥(pyramid).
底面
侧面
顶点
侧棱
3、棱锥的表示方法:用表示顶点和底面的字母表示,如四棱锥S-ABCD。
五棱锥
三棱锥
四棱锥
(四面体)
4、特殊的棱锥-正棱锥
定义:如果一个棱锥的底面是正多边形,
并且顶点在底面的射影是底面中心
正三棱锥
正五棱锥
5、正多面体:
定义:每个面都是有相同边数正多边形,且以每个顶点为其一端都有相同数目的棱的凸多面体,叫做正多面体。
三、棱台的结构特征
定义:用一个平行于棱锥底面的的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台.
上底面
下底面
四棱台
上底面
下底面
侧面
侧棱
顶点
2、由三棱锥、四棱锥、五棱锥…截得的棱台,分别叫做三棱台,四棱台,五棱台…
3、棱台的表示法:
棱台用表示上、下底面各顶点的字母来表示,棱台ABCD-A1B1C1D1 。
题型一 棱柱的结构特征
【例1】 下列说法正确的是( )
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.各侧面都是正方形的四棱柱一定是正方体
D.九棱柱有9条侧棱,9个侧面,侧面均为平行四边形
答案 D
题型二 棱锥、棱台的结构特征
【例2】 (1)下列三种叙述,正确的有( )
①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;
②两个面平行且相似,其余各面都是梯形的多面体是棱台;
③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.
A.0个 B.1个 C.2个 D.3个
(2)下列说法中,正确的是( )
①棱锥的各个侧面都是三角形;
②四面体的任何一个面都可以作为棱锥的底面;
③棱锥的侧棱平行.
A.① B.①② C.② D.③
B
A
4、下列关于多面体的说法中:
(1)底面是矩形的直棱柱是长方体;
(2)底面是正方形的棱锥是正四棱锥;
(3)两底面都是正方形的棱台是正棱台;
(4)正四棱柱就是正方体;
其中正确的是_________
(1)
5、下列图中,不是正方体的表面展开图的是( )
A
B
C
D
C
6、下图不是棱柱的展开图的是( )
A
B
C
D
C
7.正三棱锥A-BCD的底面边长为2a,侧面的顶角为300,E、F分别是AC、AD上的动点,求截面三角形BEF周长的最小值。
8.1 基本立体图形--多面体
牟和方盖
这里的“牟”意思是相同.“盖”意思是伞.“牟合方盖”就是指两个面合在一起的两个相同的方伞.它是由一个正方体出发,先用竖直方向的内切圆柱截正方体,得到一个圆柱体,再用水平方向的圆柱再截一次,两个圆柱的共同部分所形成的几何体,就叫做“牟合方盖” .
我们生活的空间是三维空间,触摸到的物体几乎都和几何体有关,在小学、初中我们接触过一些特殊的几何体:正方体、圆柱体、球等。在生活中,我们也常见到一些建筑物,它们实际上是由几种空间几何体组合在一起形成的,今天我们一起来研究其中一些基本的空间几何体.
空间几何体:
对于空间的物体,如果只考虑它的的形状、大小和位置,而不考虑物体的其他因素,从中抽象出来的空间图形叫做空间几何体
比较图中物体,围成它们的面有什么不同?如何分类?
(7)
(8)
(5)
(4)
(3)
(2)
(6)
(1)
空间几何体
多面体:若干个平面多边形围成的几何体.
空间几何体
面
棱
顶点
轴
空间几何体
旋转体:由一个平面多边形(包括直线)绕它所在平面内的一条定直线旋转形成的曲面叫做旋转面,封闭的旋转面围成的几何体.
空间几何体的分类:
1.多面体:由若干平面多边形围成的几何体
2.旋转体:由一个平面图形绕它所在的平面内的一条定直线旋转所成的封闭几何体
空间几何体的定义:
如果只考虑物体的形状和大小,而不考虑其它因素,那么这些由物体抽象出来的空间图形就叫做空间几何体
归纳小结
从多面体组成元素的形状、位置关系入手,进一步认识它们
多面体:
棱柱
棱锥
(1)有两个面互相平行,(2)其余各面都是四边形,(3)每相邻两个四边形的公共边都互相平行,
由这些面所围成的几何体叫棱柱(prism)。
有两个面是对应边平行的全等多边形,其余面都是平行四边形的几何体是否是棱柱?
在数学史上,对棱柱的定义也走过一些弯路,如:《几何原本》中定义一个棱柱是一个立体图形,它是由一些平面构成的,其中有两个面是相对的、相等的、相似且平行的,其他各个面都是平行四边形。
波利亚棱柱反例
有两个面是对应边平行的全等多边形,其余面都是平行四边形的几何体是否是棱柱?
底面
侧面
侧棱
顶点
六棱柱:
棱柱的底面互相平行且相等
棱柱的侧面都是平行四边形
棱柱的侧棱都是平行且相等
棱柱的分类:棱柱的底面可以是三角形、四边形、五边形、 …… 我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……
三棱柱
四棱柱
五棱柱
棱柱的分类二:(根据侧棱与底面的关系):
斜棱柱: 侧棱不垂直于底面的棱柱.
直棱柱: 侧棱垂直于底面的棱柱叫做直棱柱
棱柱概念的推广
(1)斜棱柱:侧棱不垂直于底面的棱柱叫做斜棱柱.
(2)直棱柱:侧棱垂直于底面的棱柱叫做直棱柱.
(3)正棱柱:底面是正多边形的直棱柱叫做正棱柱.
(4)平行六面体:底面是平行四边形的四棱柱叫做平行六面体,即平行六面体的六个面都是平行四边形.
(5)长方体:底面是矩形的直棱柱叫做长方体.
(6)正方体:棱长都相等的长方体叫做正方体.
四棱柱的分类
A
B
F
E
G
C
四棱柱
平行六面体
直平行六面体
长方体
正四棱柱
正方体
D
(1) 一个面是多边形
(2) 其余各面都是有一个公共顶点的三角形,
由这些面围成的的多面体叫做棱锥(pyramid).
底面
侧面
顶点
侧棱
3、棱锥的表示方法:用表示顶点和底面的字母表示,如四棱锥S-ABCD。
五棱锥
三棱锥
四棱锥
(四面体)
4、特殊的棱锥-正棱锥
定义:如果一个棱锥的底面是正多边形,
并且顶点在底面的射影是底面中心
正三棱锥
正五棱锥
5、正多面体:
定义:每个面都是有相同边数正多边形,且以每个顶点为其一端都有相同数目的棱的凸多面体,叫做正多面体。
三、棱台的结构特征
定义:用一个平行于棱锥底面的的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台.
上底面
下底面
四棱台
上底面
下底面
侧面
侧棱
顶点
2、由三棱锥、四棱锥、五棱锥…截得的棱台,分别叫做三棱台,四棱台,五棱台…
3、棱台的表示法:
棱台用表示上、下底面各顶点的字母来表示,棱台ABCD-A1B1C1D1 。
题型一 棱柱的结构特征
【例1】 下列说法正确的是( )
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.各侧面都是正方形的四棱柱一定是正方体
D.九棱柱有9条侧棱,9个侧面,侧面均为平行四边形
答案 D
题型二 棱锥、棱台的结构特征
【例2】 (1)下列三种叙述,正确的有( )
①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;
②两个面平行且相似,其余各面都是梯形的多面体是棱台;
③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.
A.0个 B.1个 C.2个 D.3个
(2)下列说法中,正确的是( )
①棱锥的各个侧面都是三角形;
②四面体的任何一个面都可以作为棱锥的底面;
③棱锥的侧棱平行.
A.① B.①② C.② D.③
B
A
4、下列关于多面体的说法中:
(1)底面是矩形的直棱柱是长方体;
(2)底面是正方形的棱锥是正四棱锥;
(3)两底面都是正方形的棱台是正棱台;
(4)正四棱柱就是正方体;
其中正确的是_________
(1)
5、下列图中,不是正方体的表面展开图的是( )
A
B
C
D
C
6、下图不是棱柱的展开图的是( )
A
B
C
D
C
7.正三棱锥A-BCD的底面边长为2a,侧面的顶角为300,E、F分别是AC、AD上的动点,求截面三角形BEF周长的最小值。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
