人教版必修一 4.5.1方程的根与函数的零点 课件(33张PPT)
文档属性
| 名称 | 人教版必修一 4.5.1方程的根与函数的零点 课件(33张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-27 00:00:00 | ||
图片预览









文档简介
(共33张PPT)
我国古代数学家已比较系统地解决了部分方程的求解的问题.如约公元50~100年编成的《九章算术》,就给出了求一次方程、二次方程根的具体方法……
这比西方要早三百多年。
11世纪,北宋数学家贾宪给出了三次及三次以上的方程的解法。
13世纪,南宋数学家秦九韶给出了求任意次代数方程的正根的解法,是具有世界先驱意义的首创。
学会从不同的角度看问题
一次函数
二元一次方程
一条直线
——数的角度
——形的角度
4.5.1方程的解与函数的零点
对于函数 y=f(x),我们把使 f(x)=0 的实数x叫做函数 y=f(x) 的零点.
函数零点的定义:
数的角度:
形的角度:
函数
的零点就是方程
的解.
函数
的零点就是它的图象与 轴公共点
的横坐标.
方程 有实数解
函数 有零点
的图象与 轴有公共点
数的角度
形的角度
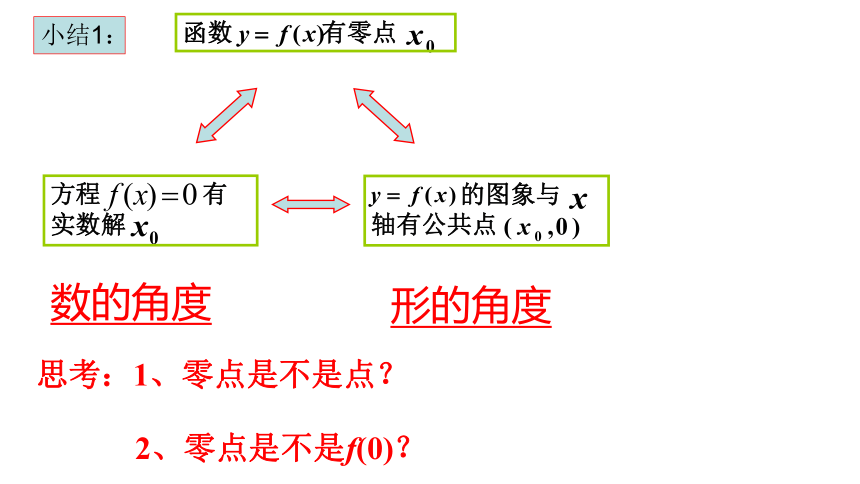
小结1:
思考:1、零点是不是点?
2、零点是不是f(0)?
例1 求下列函数的零点
求函数零点的步骤:
(1)令f(x)=0;
(2)解方程f(x)=0;
(3)写出零点
以上四个问题中的零点,可以通过直接解方程轻松得到答案,那么对于不能用公式法求根的方程,我们又该如何处理呢?
探究:函数存在零点的图象特征,以及零点附近函数值的变化规律
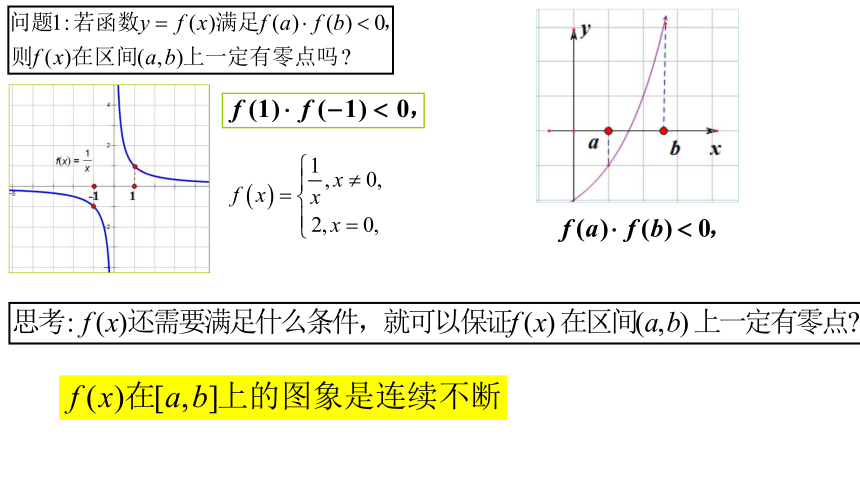
判断函数 在区间 是否存在零点?
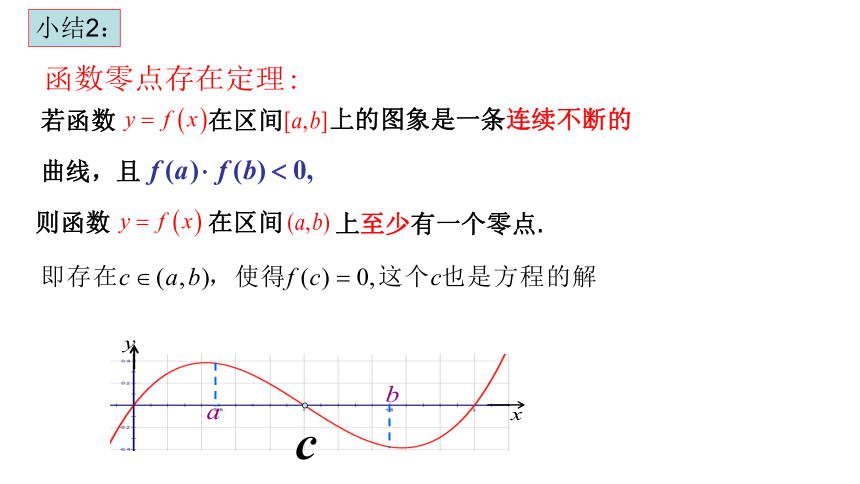
则函数
在区间
上至少有一个零点.
若函数
上的图象是一条连续不断的
在区间
曲线,且
小结2:
温馨提示:
有时感觉零点存在定理“失效”了,其实是区间太“大”了。
小结3:
3.已知函数 , ,
的零点依次是 ,则( )
A.
B.
C.
D.
B
6.已知连续函数 ,有 ,
则 ( )
A.在区间 上可能没有零点
B.在区间 上可能有三个零点
C.在区间 上至多有一个有零点
D.在区间 上不可能有两个零点
B
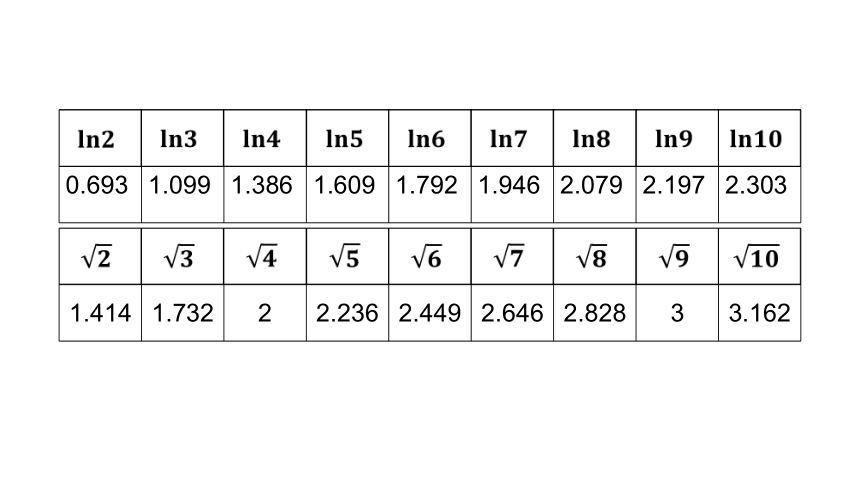
例7 求证函数f(x)=lnx+2x-6在(2,3)有且只有一个零点.
判断方程㏑x = - x2 + 3实根的个数?
练习:
练习:已知函数f(x)的图象是连续不断的, 且有如下的x,f(x)对应值表:
–26
–12
–5
11
–7
9
23
f (x)
7
6
5
4
3
2
1
x
那么该函数在区间[1,6]上有( )零点.
A、只有3个 B、至少有3个
C、至多有3个 D、无法确定
B
小结6:
1、若函数 有3个零点
则
针对训练:
课堂总结
知识上的收获:
函数零点的定义
函数的零点存在定理
零点个数的判断方法
思想方法的丰富:
函数与方程
由特殊到一般
数形结合
我国古代数学家已比较系统地解决了部分方程的求解的问题.如约公元50~100年编成的《九章算术》,就给出了求一次方程、二次方程根的具体方法……
这比西方要早三百多年。
11世纪,北宋数学家贾宪给出了三次及三次以上的方程的解法。
13世纪,南宋数学家秦九韶给出了求任意次代数方程的正根的解法,是具有世界先驱意义的首创。
学会从不同的角度看问题
一次函数
二元一次方程
一条直线
——数的角度
——形的角度
4.5.1方程的解与函数的零点
对于函数 y=f(x),我们把使 f(x)=0 的实数x叫做函数 y=f(x) 的零点.
函数零点的定义:
数的角度:
形的角度:
函数
的零点就是方程
的解.
函数
的零点就是它的图象与 轴公共点
的横坐标.
方程 有实数解
函数 有零点
的图象与 轴有公共点
数的角度
形的角度
小结1:
思考:1、零点是不是点?
2、零点是不是f(0)?
例1 求下列函数的零点
求函数零点的步骤:
(1)令f(x)=0;
(2)解方程f(x)=0;
(3)写出零点
以上四个问题中的零点,可以通过直接解方程轻松得到答案,那么对于不能用公式法求根的方程,我们又该如何处理呢?
探究:函数存在零点的图象特征,以及零点附近函数值的变化规律
判断函数 在区间 是否存在零点?
则函数
在区间
上至少有一个零点.
若函数
上的图象是一条连续不断的
在区间
曲线,且
小结2:
温馨提示:
有时感觉零点存在定理“失效”了,其实是区间太“大”了。
小结3:
3.已知函数 , ,
的零点依次是 ,则( )
A.
B.
C.
D.
B
6.已知连续函数 ,有 ,
则 ( )
A.在区间 上可能没有零点
B.在区间 上可能有三个零点
C.在区间 上至多有一个有零点
D.在区间 上不可能有两个零点
B
例7 求证函数f(x)=lnx+2x-6在(2,3)有且只有一个零点.
判断方程㏑x = - x2 + 3实根的个数?
练习:
练习:已知函数f(x)的图象是连续不断的, 且有如下的x,f(x)对应值表:
–26
–12
–5
11
–7
9
23
f (x)
7
6
5
4
3
2
1
x
那么该函数在区间[1,6]上有( )零点.
A、只有3个 B、至少有3个
C、至多有3个 D、无法确定
B
小结6:
1、若函数 有3个零点
则
针对训练:
课堂总结
知识上的收获:
函数零点的定义
函数的零点存在定理
零点个数的判断方法
思想方法的丰富:
函数与方程
由特殊到一般
数形结合
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
