人教版必修一 4.4.3几类不同增长的函数模型 课件(20张PPT)
文档属性
| 名称 | 人教版必修一 4.4.3几类不同增长的函数模型 课件(20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-27 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
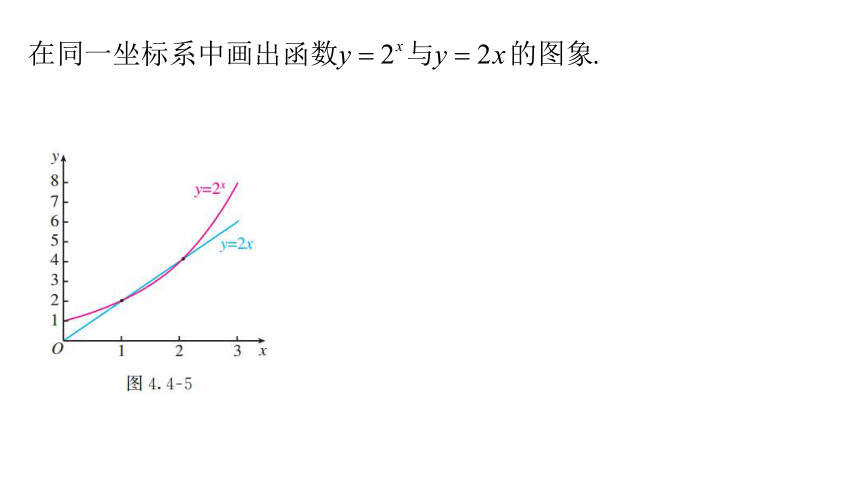
4.4.3几类不同增长的函数模型
(一次、幂、指、对)函数模型的增长差异性
1、三种常见函数模型的增长差异
函数
性质 y=ax(a>1) y=logax(a>1) y=kx(k>0)
在(0,+∞)上的增减性
图象的变化 随x的增大逐渐变“陡” 随x的增大逐渐趋于平缓 增长速度不变
形象描述 指数爆炸 对数增长 直线上升
增长速度
增长结果
增函数
增函数
增函数
1、三种常见函数模型的增长差异
函数
性质 y=ax(a>1) y=logax(a>1) y=kx(k>0)
在(0,+∞)上的增减性
图象的变化 随x的增大逐渐变“陡” 随x的增大逐渐趋于稳定 增长速度不变
形象描述 指数爆炸 对数增长 直线上升
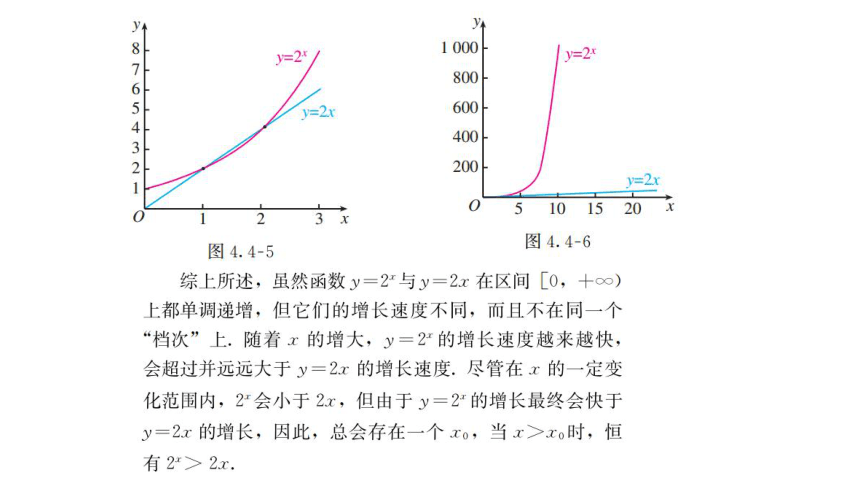
增长速度 y=ax(a>1)的增长速度最终都会大大超过___________的增长速度;
增长结果
存在一个x0,当x>x0时,有_____________
增函数
增函数
增函数
y=kx(k>0)
ax>kx
1、三种常见函数模型的增长差异
函数
性质 y=ax(a>1) y=logax(a>1) y=kx(k>0)
在(0,+∞)上的增减性
图象的变化 随x的增大逐渐变“陡” 随x的增大逐渐趋于稳定 增长速度不变
形象描述 指数爆炸 对数增长 直线上升
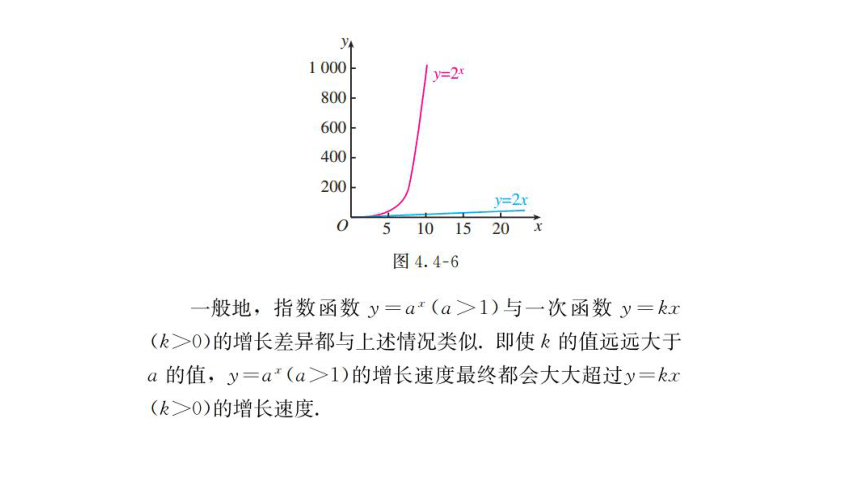
增长速度 y=ax(a>1)的增长速度最终都会大大超过___________的增长速度;
增长结果
存在一个x0,当x>x0时,有_____________
增函数
增函数
增函数
y=kx(k>0)
ax>kx>logax
确定函数模型
利用数据表格、函数图象讨论模型
体会直线上升、指数爆炸、对数增长等不同函数类型的增长含义
题型二 对数函数模型
(1)当一条鲑鱼的耗氧量是900个单位时,它的游速是多少?
(2)某条鲑鱼想把游速提高1 m/s,那么它的耗氧量的单位数是原来的多少倍?
所以当一条鲑鱼的耗氧量是900个单位时,它的游速是1 m/s.
2.2014年我国人口总数约为14亿,如果人口的自然年增长率控制在1.25%,则预计________年我国人口将首次超过20亿(lg 2≈0.301 0,lg 3≈0.477 1,lg 7≈0.845 1).
答案 2 043
规律方法 指数型、对数型函数问题的类型及解法
(1)指数函数模型:y=max(a>0且a≠1,m≠0),在实际问题中,有关人口增长、银行利率、细胞分裂等增长率问题都可用指数型函数模型来表示.
(2)对数函数模型:y=mlogax+c(m≠0,a>0且a≠1),对数函数模型一般给出函数关系式,然后利用对数的运算求解.
(3)指数型、对数型函数应用题的解题思路:①依题意,找出或建立数学模型,②依实际情况确立解析式中的参数,③依题设数据解决数学问题,④得出结论.
3、指数增长或衰减模型
将一张报纸连续对折,折叠次数x与对应的层数y间存在什么关系?对折后的面积S(设原面积为1)与折叠的次数有怎样的关系?
4.4.3几类不同增长的函数模型
(一次、幂、指、对)函数模型的增长差异性
1、三种常见函数模型的增长差异
函数
性质 y=ax(a>1) y=logax(a>1) y=kx(k>0)
在(0,+∞)上的增减性
图象的变化 随x的增大逐渐变“陡” 随x的增大逐渐趋于平缓 增长速度不变
形象描述 指数爆炸 对数增长 直线上升
增长速度
增长结果
增函数
增函数
增函数
1、三种常见函数模型的增长差异
函数
性质 y=ax(a>1) y=logax(a>1) y=kx(k>0)
在(0,+∞)上的增减性
图象的变化 随x的增大逐渐变“陡” 随x的增大逐渐趋于稳定 增长速度不变
形象描述 指数爆炸 对数增长 直线上升
增长速度 y=ax(a>1)的增长速度最终都会大大超过___________的增长速度;
增长结果
存在一个x0,当x>x0时,有_____________
增函数
增函数
增函数
y=kx(k>0)
ax>kx
1、三种常见函数模型的增长差异
函数
性质 y=ax(a>1) y=logax(a>1) y=kx(k>0)
在(0,+∞)上的增减性
图象的变化 随x的增大逐渐变“陡” 随x的增大逐渐趋于稳定 增长速度不变
形象描述 指数爆炸 对数增长 直线上升
增长速度 y=ax(a>1)的增长速度最终都会大大超过___________的增长速度;
增长结果
存在一个x0,当x>x0时,有_____________
增函数
增函数
增函数
y=kx(k>0)
ax>kx>logax
确定函数模型
利用数据表格、函数图象讨论模型
体会直线上升、指数爆炸、对数增长等不同函数类型的增长含义
题型二 对数函数模型
(1)当一条鲑鱼的耗氧量是900个单位时,它的游速是多少?
(2)某条鲑鱼想把游速提高1 m/s,那么它的耗氧量的单位数是原来的多少倍?
所以当一条鲑鱼的耗氧量是900个单位时,它的游速是1 m/s.
2.2014年我国人口总数约为14亿,如果人口的自然年增长率控制在1.25%,则预计________年我国人口将首次超过20亿(lg 2≈0.301 0,lg 3≈0.477 1,lg 7≈0.845 1).
答案 2 043
规律方法 指数型、对数型函数问题的类型及解法
(1)指数函数模型:y=max(a>0且a≠1,m≠0),在实际问题中,有关人口增长、银行利率、细胞分裂等增长率问题都可用指数型函数模型来表示.
(2)对数函数模型:y=mlogax+c(m≠0,a>0且a≠1),对数函数模型一般给出函数关系式,然后利用对数的运算求解.
(3)指数型、对数型函数应用题的解题思路:①依题意,找出或建立数学模型,②依实际情况确立解析式中的参数,③依题设数据解决数学问题,④得出结论.
3、指数增长或衰减模型
将一张报纸连续对折,折叠次数x与对应的层数y间存在什么关系?对折后的面积S(设原面积为1)与折叠的次数有怎样的关系?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
