第13章轴对称 课题学习 最短路径问题 课件(11张PPT)
文档属性
| 名称 | 第13章轴对称 课题学习 最短路径问题 课件(11张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 09:56:17 | ||
图片预览




文档简介
(共11张PPT)
己1总纪教肩
2世有
W,27GG⊙
基础过关
逐点击破
知识点①
利用轴对称确定最短路径
1.如图,在△ABC中,AB=AC,AD,CE是△ABC的两
条中线,P是AD上一个动点,则下列线段的长度等
于BP+EP的最小值的是
(B)
A.BC
B.CE
C.AD
D.AC
B
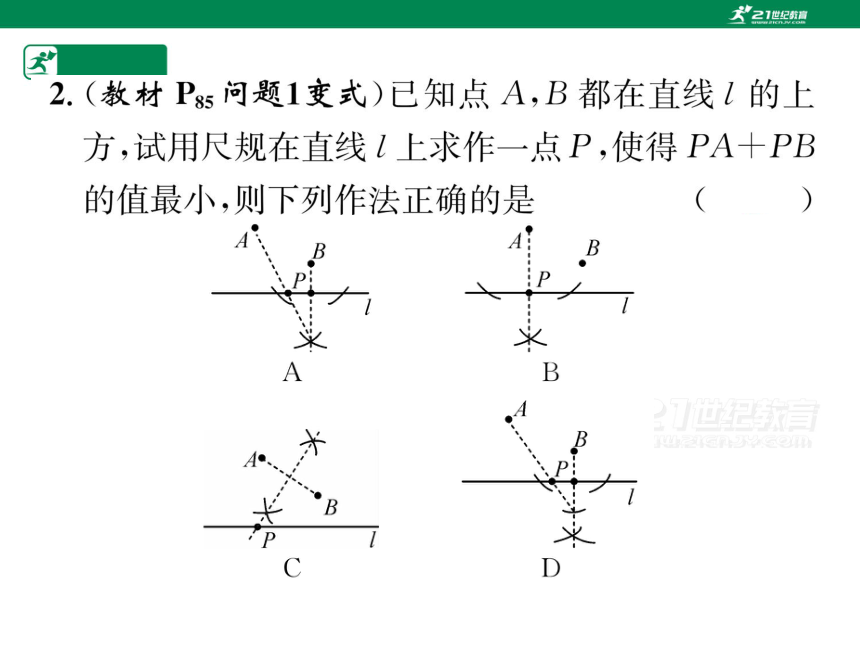
2.(教材P5问题1变式)已知点A,B都在直线l的上
方,试用尺规在直线I上求作一点P,使得PA十PB
的值最小,则下列作法正确的是
(D)
A
知识点②利用平移确定最短路径
3.如图,要在一条河上架一座桥MN(河的两岸互相
平行,桥与河岸垂直),在如下四种方案中,使得从
E到F的路程最短的是
(B
能力提升
整合运用
4.如图,在四边形ABCD中,AB∥CD,AD⊥AB,点
P是AD上的一个动点,要使PC十PB最小,则点
P应满足
(D)
A.PB-PC
D
B.PA-PD
C.∠BPC=90°
B
D.∠APB=∠DPC
5.如图,∠AOB的边OA上有M,N两点,在∠AOB
的平分线OC上找一点P,使MP+VP最小,则下
列作法正确的是
(D)
6.如图,已知∠AOB=15°,点M在边OB上,且OM=
4,点N和点P分别是OM和OA上的一个动点,则
PM+PN的最小值为
(B)
P一A
NM B
A.1
B.2
C.3
D.4
7.如图,小河边有两个村庄A,B,要在河边建一个自
来水厂向A村与B村供水
(1)若要使水厂到A,B村的距离相等,则应选择在
哪建厂?
(2)若要使水厂到A,B村的水管最省料,则应选择
在哪建厂?
解:(1)连接AB,作AB的垂直平分
线交EF于点M,点M即为所求;
(2)作点A关于EF的对称点A',连
接A'B,交EF于点C,点C即为
所求.
8.如图,在四边形ABCD中,∠BAD=120°,∠B=
∠D=90°,在BC,CD上分别找一点M,N,使
△AMN的周长最小,求∠AMN+∠ANM的
度数,
解:作点A关于BC和CD的
对称点A',A",连接A'A",交
B
BC于点M,交CD于点N,连
接AM,AN,则A'A"等于
△AMN周长的最小值,
.∠A'=∠MAA',∠NAD=∠A"
.∠DAB=120°,
.∠A'+∠A"=180°-120°=60°.
.'∠A'+∠MAA'=∠AMN,
∠NAD+∠A"=∠ANM,
.∴∠AMN+∠ANM=∠A'+∠MAA'+∠NAD
+∠A"=2(∠A'+∠A")=2×60°=120°.
己1总纪教肩
2世有
W,27GG⊙
基础过关
逐点击破
知识点①
利用轴对称确定最短路径
1.如图,在△ABC中,AB=AC,AD,CE是△ABC的两
条中线,P是AD上一个动点,则下列线段的长度等
于BP+EP的最小值的是
(B)
A.BC
B.CE
C.AD
D.AC
B
2.(教材P5问题1变式)已知点A,B都在直线l的上
方,试用尺规在直线I上求作一点P,使得PA十PB
的值最小,则下列作法正确的是
(D)
A
知识点②利用平移确定最短路径
3.如图,要在一条河上架一座桥MN(河的两岸互相
平行,桥与河岸垂直),在如下四种方案中,使得从
E到F的路程最短的是
(B
能力提升
整合运用
4.如图,在四边形ABCD中,AB∥CD,AD⊥AB,点
P是AD上的一个动点,要使PC十PB最小,则点
P应满足
(D)
A.PB-PC
D
B.PA-PD
C.∠BPC=90°
B
D.∠APB=∠DPC
5.如图,∠AOB的边OA上有M,N两点,在∠AOB
的平分线OC上找一点P,使MP+VP最小,则下
列作法正确的是
(D)
6.如图,已知∠AOB=15°,点M在边OB上,且OM=
4,点N和点P分别是OM和OA上的一个动点,则
PM+PN的最小值为
(B)
P一A
NM B
A.1
B.2
C.3
D.4
7.如图,小河边有两个村庄A,B,要在河边建一个自
来水厂向A村与B村供水
(1)若要使水厂到A,B村的距离相等,则应选择在
哪建厂?
(2)若要使水厂到A,B村的水管最省料,则应选择
在哪建厂?
解:(1)连接AB,作AB的垂直平分
线交EF于点M,点M即为所求;
(2)作点A关于EF的对称点A',连
接A'B,交EF于点C,点C即为
所求.
8.如图,在四边形ABCD中,∠BAD=120°,∠B=
∠D=90°,在BC,CD上分别找一点M,N,使
△AMN的周长最小,求∠AMN+∠ANM的
度数,
解:作点A关于BC和CD的
对称点A',A",连接A'A",交
B
BC于点M,交CD于点N,连
接AM,AN,则A'A"等于
△AMN周长的最小值,
.∠A'=∠MAA',∠NAD=∠A"
.∠DAB=120°,
.∠A'+∠A"=180°-120°=60°.
.'∠A'+∠MAA'=∠AMN,
∠NAD+∠A"=∠ANM,
.∴∠AMN+∠ANM=∠A'+∠MAA'+∠NAD
+∠A"=2(∠A'+∠A")=2×60°=120°.
