13.3.1 等腰三角形(第二课时)
文档属性
| 名称 | 13.3.1 等腰三角形(第二课时) |  | |
| 格式 | zip | ||
| 文件大小 | 107.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-19 16:24:21 | ||
图片预览





文档简介
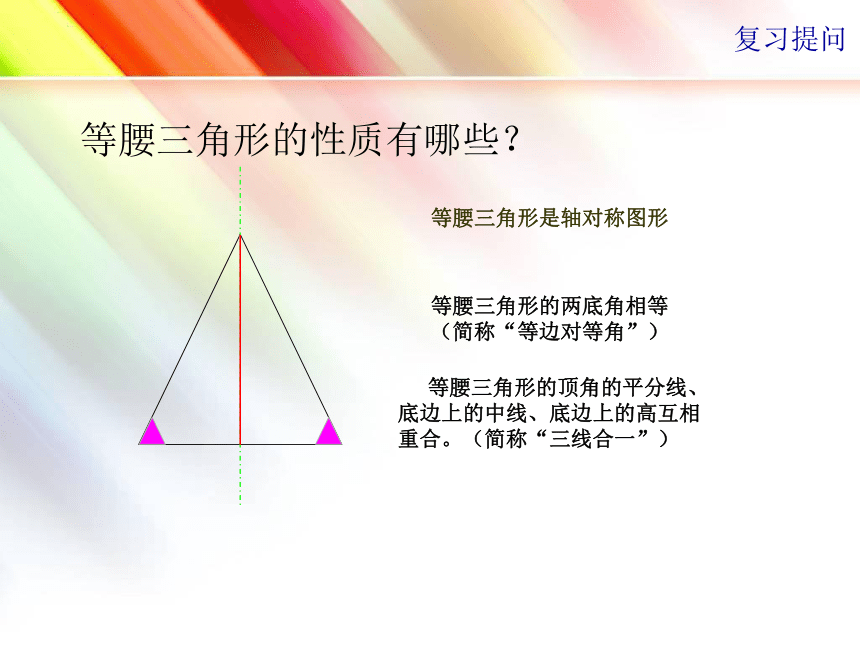
课件15张PPT。13.3.1等腰三角形(第二课时)复习提问等腰三角形的性质有哪些?等腰三角形是轴对称图形等腰三角形的两底角相等(简称“等边对等角”) 等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合。(简称“三线合一”) 在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?想一想ABC它们所对的边相等 如果一个三角形有两个角相等,那么这两个角所对的边也相等。你能证明吗?已知:在△ABC中,∠B = ∠C求证:AB=AC已知:△ABC中,∠B=∠C求证:AB=AC证明:作∠BAC的平分线AD在△ BAD和△ CAD中,∠B=∠C,
∠1=∠2,
AD=AD∴ △ BAD≌ △ CAD(AAS)∴AB=AC(全等三角形的对应边相等) 12思考:作底边上的高可以吗?作底边中线呢?例题讲解等腰三角形的判定方法: 如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成:等角对等边”)。
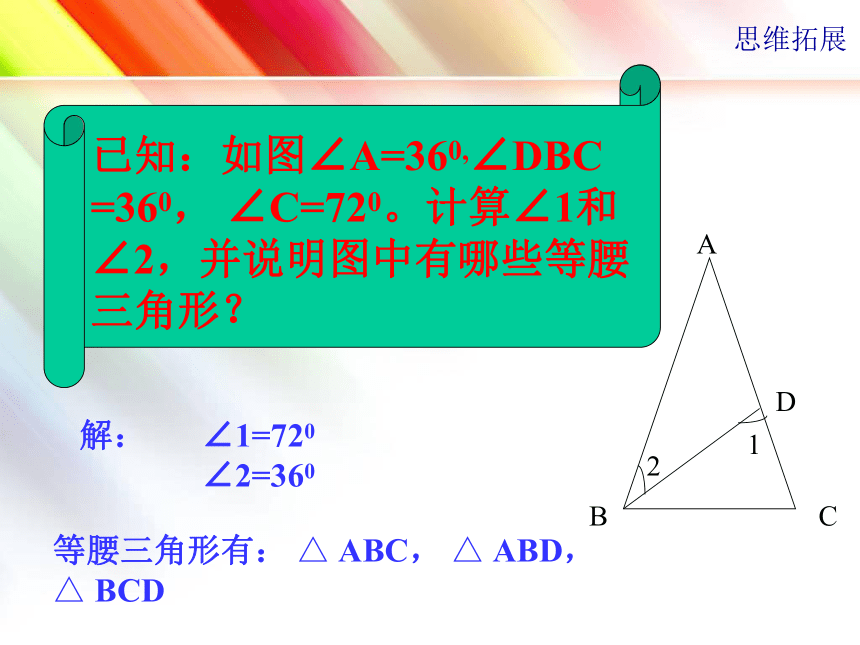
思维拓展解:∠1=720 ∠2=360等腰三角形有: △ ABC, △ ABD, △ BCD例1 :求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。从求证看:要证AB=AC,需证∠B=∠C,
分析:
从已知看:因为∠1=∠2,AD∥BC
可以找出∠B,∠C与的关系。
例题讲解证明:∵AD∥BC,
∴∠1=∠B(两直线平行,
同位角相等),
∠2=∠C(两直线平行,
内错角相等)。
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边)。例题讲解自己试一试! 用尺规画一个等腰三角形ABC,使得底边BC为3cm,底边上的高AD为5cm。 用尺规画一个等腰三角形ABC,使得底边BC为3cm,底边上的高AD为5cm。例2:如图, ⊿ABC中,AB=AC,BD平分∠ABC,CE平分∠ACB,BD与CE交于点O,试说明⊿BOC是等腰三角形。AEDBCO分析:此题主要考察等腰三角形的判定与性质的应用,由AB=AC可得∠ABC= ∠ACB,又由于BD,CE分别是这两个角的平分线,可得∠OBC= ∠OCB,则⊿BOC为等腰三角形。解:∵AB=AC
∴ ∠ABC= ∠ACB
∵BD平分∠ABC,CE平分∠ACB
∴ ∠OBC=? ∠ ABC, ∠OCB=? ∠ACB
∴ ∠OBC= ∠OCB
∴ ⊿BOC为等腰三角形2.如图,在△ABC中,AB=AC,∠B=36O,D、E是BC上的两点,且∠ADE=∠AED=2∠BAD,则图中的等腰三角形共有( )个。
A.3个 B.4个 C.5个 D.6个1.如图,△ABC中,AB=AC,∠A=36°,BD平分∠ABC,
DE∥BC,则图形中共有等腰三角形( )
A.2个 B.3个 C.4个 D.5个DD习题精练3.如图,△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F
求证:EF=EB+FC.
1、等腰三角形的判定方法有下列几种: 。2、等腰三角形的判定定理与性质定理的区别是 。3、运用等腰三角形的判定定理时,应注意 。①定义,②判定定理 条件和结论刚好相反。在同一个三角形中课堂小结课后作业谢谢!
∠1=∠2,
AD=AD∴ △ BAD≌ △ CAD(AAS)∴AB=AC(全等三角形的对应边相等) 12思考:作底边上的高可以吗?作底边中线呢?例题讲解等腰三角形的判定方法: 如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成:等角对等边”)。
思维拓展解:∠1=720 ∠2=360等腰三角形有: △ ABC, △ ABD, △ BCD例1 :求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。从求证看:要证AB=AC,需证∠B=∠C,
分析:
从已知看:因为∠1=∠2,AD∥BC
可以找出∠B,∠C与的关系。
例题讲解证明:∵AD∥BC,
∴∠1=∠B(两直线平行,
同位角相等),
∠2=∠C(两直线平行,
内错角相等)。
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边)。例题讲解自己试一试! 用尺规画一个等腰三角形ABC,使得底边BC为3cm,底边上的高AD为5cm。 用尺规画一个等腰三角形ABC,使得底边BC为3cm,底边上的高AD为5cm。例2:如图, ⊿ABC中,AB=AC,BD平分∠ABC,CE平分∠ACB,BD与CE交于点O,试说明⊿BOC是等腰三角形。AEDBCO分析:此题主要考察等腰三角形的判定与性质的应用,由AB=AC可得∠ABC= ∠ACB,又由于BD,CE分别是这两个角的平分线,可得∠OBC= ∠OCB,则⊿BOC为等腰三角形。解:∵AB=AC
∴ ∠ABC= ∠ACB
∵BD平分∠ABC,CE平分∠ACB
∴ ∠OBC=? ∠ ABC, ∠OCB=? ∠ACB
∴ ∠OBC= ∠OCB
∴ ⊿BOC为等腰三角形2.如图,在△ABC中,AB=AC,∠B=36O,D、E是BC上的两点,且∠ADE=∠AED=2∠BAD,则图中的等腰三角形共有( )个。
A.3个 B.4个 C.5个 D.6个1.如图,△ABC中,AB=AC,∠A=36°,BD平分∠ABC,
DE∥BC,则图形中共有等腰三角形( )
A.2个 B.3个 C.4个 D.5个DD习题精练3.如图,△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F
求证:EF=EB+FC.
1、等腰三角形的判定方法有下列几种: 。2、等腰三角形的判定定理与性质定理的区别是 。3、运用等腰三角形的判定定理时,应注意 。①定义,②判定定理 条件和结论刚好相反。在同一个三角形中课堂小结课后作业谢谢!
