5.3《圆的面积》(课件)-六年级上册数学青岛版(共25张PPT)
文档属性
| 名称 | 5.3《圆的面积》(课件)-六年级上册数学青岛版(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-27 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
圆的面积
圆形中心舞台的直径是20米。
中心舞台的面积是多少平方米?
一、情境导入
从图中,你知道了哪些数学信息?
根据这些信息,你能提出什么问题?
2008年北京奥运会闭幕式圆形中心舞台的直径是20米,其中有一个直径是1.6米的圆形升降舞台。
3
圆形升降舞台的直径是1.6米。
升降舞台的面积是多少平方米?
求中心舞台的面积也就是求圆的面积。
中心舞台的面积是多少平方米?
二、合作探索
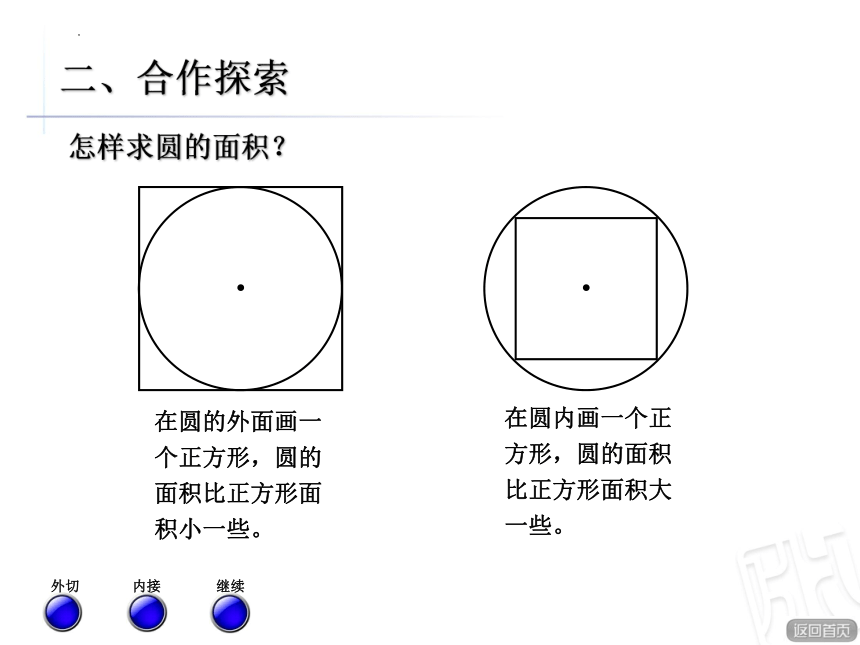
怎样求圆的面积?
可以把圆转化成已经学过的图形来研究。
怎样求圆的面积?
二、合作探索
在圆的外面画一个正方形,圆的面积比正方形面积小一些。
在圆内画一个正方形,圆的面积比正方形面积大一些。
外切
内接
继续
二、合作探索
返回
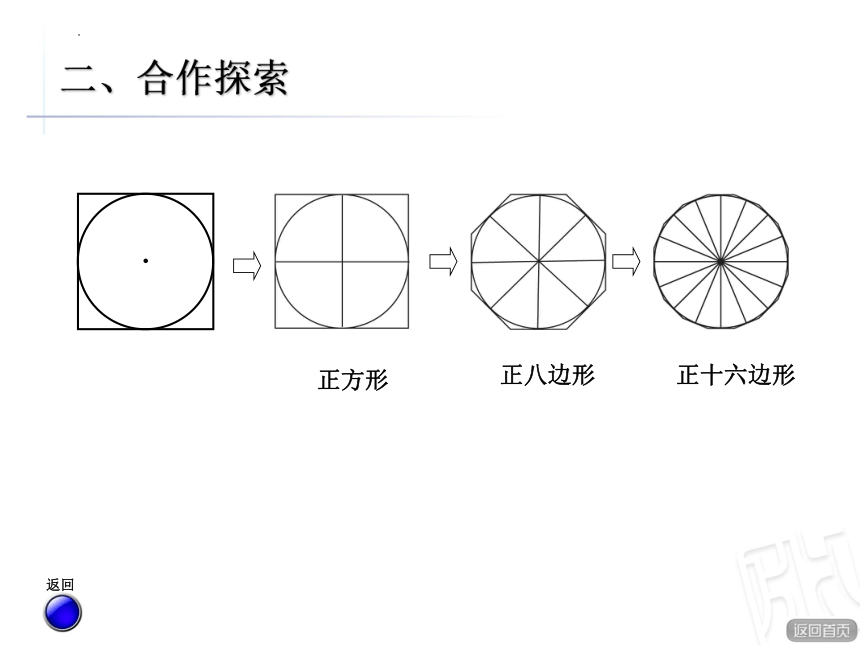
正方形
正八边形
正十六边形
二、合作探索
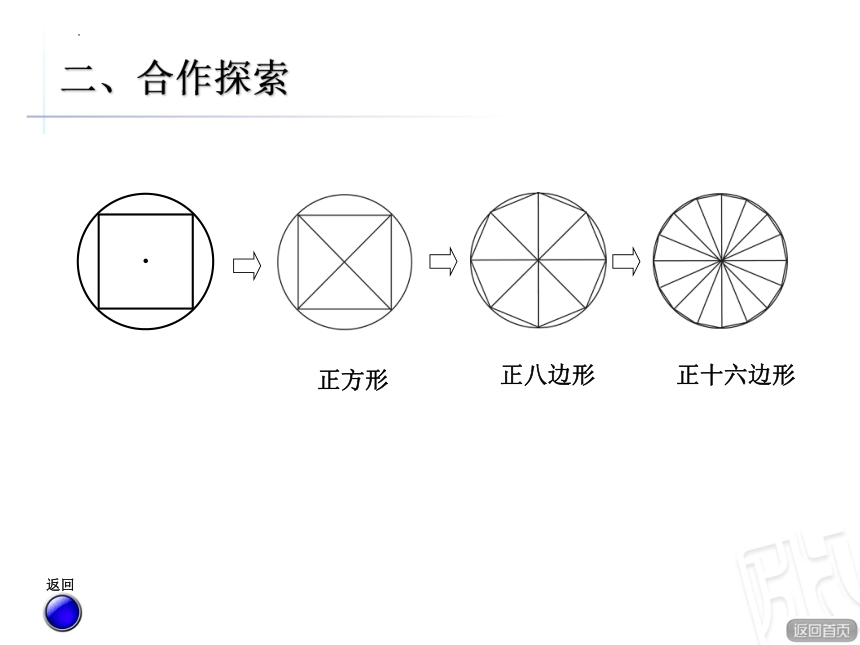
正方形
正八边形
正十六边形
返回
二、合作探索
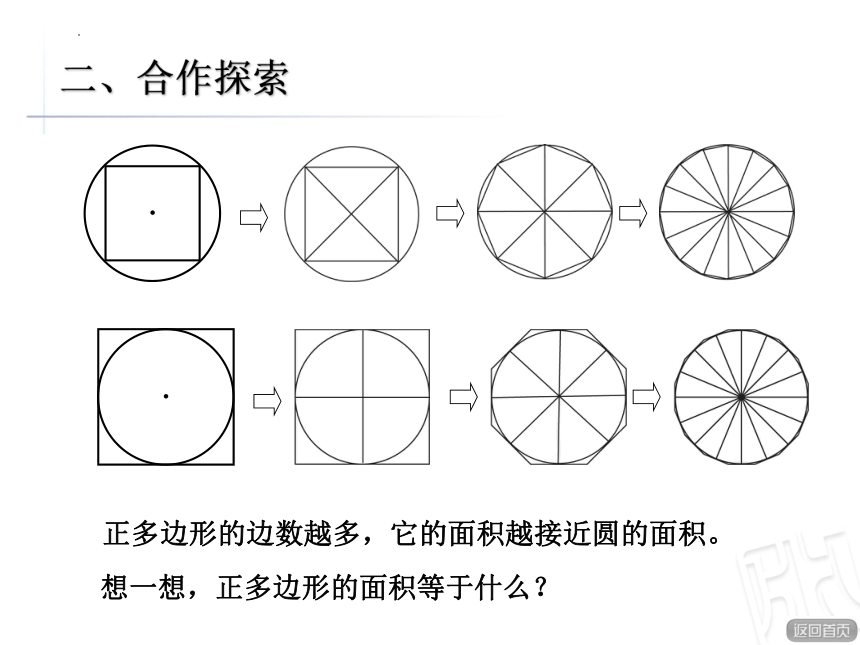
正多边形的边数越多,它的面积越接近圆的面积。
想一想,正多边形的面积等于什么?
把圆平均分成若干个小扇形,再拼一拼。
8等份
16等份
二、合作探索
32等份
64等份
继续
剪拼重组
二、合作探索
返回
剪拼重组
二、合作探索
返回
剪拼重组
二、合作探索
返回
剪拼重组
二、合作探索
返回
剪拼对比
二、合作探索
平均分的份数越多,拼成的图形越接近于长方形。
公式推导
二、合作探索
二、合作探索
答:中心舞台的面积是314平方米。
= 3.14×102
= 3.14×100
= 314(平方米)
3.14×
( )
2
20
2
中心舞台的面积是多少平方米?
圆形中心舞台的直径是20米
试一试
答:中心舞台的面积大约是2平方米。
= 3.14×0.82
= 3.14×0.64
= 2.0096
1.圆形升降舞台的直径是1.6米,升降舞台的面积大约是多少平方米?(得数保留整数)
(1.6÷2)
3.14×
2
≈2(平方米)
2.求下面各圆的面积。
试一试
O
2m
O
20mm
3.14×22
= 3.14×4
= 12.56(m2)
= 3.14×100
= 314(mm2)
3.14×
( )
2
20
2
圆的面积发展历史
有一天,刘徽在偶然中看到了石匠在切割石头,看着看着竟觉得十分有趣,就站在一边,细细地观察起来。他看到,一块方形的石头,先由石匠切去了四个角,四角的石头瞬间就有了八个角,然后再把这八个角切去,以此类推,石匠一直在把这些角一个一个地切去,直到无角可切为止。到最后,刘徽就发现,本来呈现方形的石块,早在不知不觉中变成了一个圆滑的柱子就是这样的一件小事,让刘徽瞬间茅塞顿开,他像石匠所做的那样,把圆不断分割,终于发明了“割圆术”。
圆的面积发展历史
16世纪,开普勒仿照切西瓜的方法,把圆分割成许多小扇形;不同的是,他一开始就把圆分成无穷多个小扇形。圆面积等于无穷多个小扇形面积的和。
二、合作探索
下面图形的面积是多少平方厘米?
12厘米
20厘米
=3.14×102
3.14×62
-
=3.14×100
-
3.14×36
=200.96(平方厘米)
答:这个图形的面积是200.96平方厘米。
环形的面积=外圆面积-内圆面积。
-
3.14×
( )
2
20
2
3.14×
( )
2
12
2
三、自主练习
1.一只羊被拴在草地的木桩上,绳子的长度是4米。这只羊最多可以吃到多少平方米的草?
3.14×42=50.24(平方米)
答:圆的面积是50.24平方米。
2.求下面涂色部分的面积。
三、自主练习
圆面积:
3.14×(40÷2)2
=3.14×400
=1256(平方厘米)
正方形面积:
40×40=1600(平方厘米)
1600-1256=344(平方厘米)
涂色部分面积:
三、自主练习
3.14×52=78.5(平方米)
20÷4=5(厘米)
答:圆的面积是78.5平方米。
如图,正方形的面积是20平方厘米,圆的面积是多少平方厘米?
3.如图,正方形的面积是20平方厘米,圆的面积是多少平方厘米?
回顾反思
通过本节课的学习,你有哪些收获?
作业布置
必做作业:
课本68页自主练习3.5.6.7
选做作业:
如图,已知AB=BC=CD=1厘米,求涂色部分的面积。
圆的面积
圆形中心舞台的直径是20米。
中心舞台的面积是多少平方米?
一、情境导入
从图中,你知道了哪些数学信息?
根据这些信息,你能提出什么问题?
2008年北京奥运会闭幕式圆形中心舞台的直径是20米,其中有一个直径是1.6米的圆形升降舞台。
3
圆形升降舞台的直径是1.6米。
升降舞台的面积是多少平方米?
求中心舞台的面积也就是求圆的面积。
中心舞台的面积是多少平方米?
二、合作探索
怎样求圆的面积?
可以把圆转化成已经学过的图形来研究。
怎样求圆的面积?
二、合作探索
在圆的外面画一个正方形,圆的面积比正方形面积小一些。
在圆内画一个正方形,圆的面积比正方形面积大一些。
外切
内接
继续
二、合作探索
返回
正方形
正八边形
正十六边形
二、合作探索
正方形
正八边形
正十六边形
返回
二、合作探索
正多边形的边数越多,它的面积越接近圆的面积。
想一想,正多边形的面积等于什么?
把圆平均分成若干个小扇形,再拼一拼。
8等份
16等份
二、合作探索
32等份
64等份
继续
剪拼重组
二、合作探索
返回
剪拼重组
二、合作探索
返回
剪拼重组
二、合作探索
返回
剪拼重组
二、合作探索
返回
剪拼对比
二、合作探索
平均分的份数越多,拼成的图形越接近于长方形。
公式推导
二、合作探索
二、合作探索
答:中心舞台的面积是314平方米。
= 3.14×102
= 3.14×100
= 314(平方米)
3.14×
( )
2
20
2
中心舞台的面积是多少平方米?
圆形中心舞台的直径是20米
试一试
答:中心舞台的面积大约是2平方米。
= 3.14×0.82
= 3.14×0.64
= 2.0096
1.圆形升降舞台的直径是1.6米,升降舞台的面积大约是多少平方米?(得数保留整数)
(1.6÷2)
3.14×
2
≈2(平方米)
2.求下面各圆的面积。
试一试
O
2m
O
20mm
3.14×22
= 3.14×4
= 12.56(m2)
= 3.14×100
= 314(mm2)
3.14×
( )
2
20
2
圆的面积发展历史
有一天,刘徽在偶然中看到了石匠在切割石头,看着看着竟觉得十分有趣,就站在一边,细细地观察起来。他看到,一块方形的石头,先由石匠切去了四个角,四角的石头瞬间就有了八个角,然后再把这八个角切去,以此类推,石匠一直在把这些角一个一个地切去,直到无角可切为止。到最后,刘徽就发现,本来呈现方形的石块,早在不知不觉中变成了一个圆滑的柱子就是这样的一件小事,让刘徽瞬间茅塞顿开,他像石匠所做的那样,把圆不断分割,终于发明了“割圆术”。
圆的面积发展历史
16世纪,开普勒仿照切西瓜的方法,把圆分割成许多小扇形;不同的是,他一开始就把圆分成无穷多个小扇形。圆面积等于无穷多个小扇形面积的和。
二、合作探索
下面图形的面积是多少平方厘米?
12厘米
20厘米
=3.14×102
3.14×62
-
=3.14×100
-
3.14×36
=200.96(平方厘米)
答:这个图形的面积是200.96平方厘米。
环形的面积=外圆面积-内圆面积。
-
3.14×
( )
2
20
2
3.14×
( )
2
12
2
三、自主练习
1.一只羊被拴在草地的木桩上,绳子的长度是4米。这只羊最多可以吃到多少平方米的草?
3.14×42=50.24(平方米)
答:圆的面积是50.24平方米。
2.求下面涂色部分的面积。
三、自主练习
圆面积:
3.14×(40÷2)2
=3.14×400
=1256(平方厘米)
正方形面积:
40×40=1600(平方厘米)
1600-1256=344(平方厘米)
涂色部分面积:
三、自主练习
3.14×52=78.5(平方米)
20÷4=5(厘米)
答:圆的面积是78.5平方米。
如图,正方形的面积是20平方厘米,圆的面积是多少平方厘米?
3.如图,正方形的面积是20平方厘米,圆的面积是多少平方厘米?
回顾反思
通过本节课的学习,你有哪些收获?
作业布置
必做作业:
课本68页自主练习3.5.6.7
选做作业:
如图,已知AB=BC=CD=1厘米,求涂色部分的面积。
