13.3.2 等边三角形
图片预览




文档简介
课件17张PPT。13.3.2等边三角形1、等腰三角形具有哪些性质?2、怎样判定一个三角形是等腰三角形?复习回顾:等腰三角形是轴对称图形
“等边对等角”
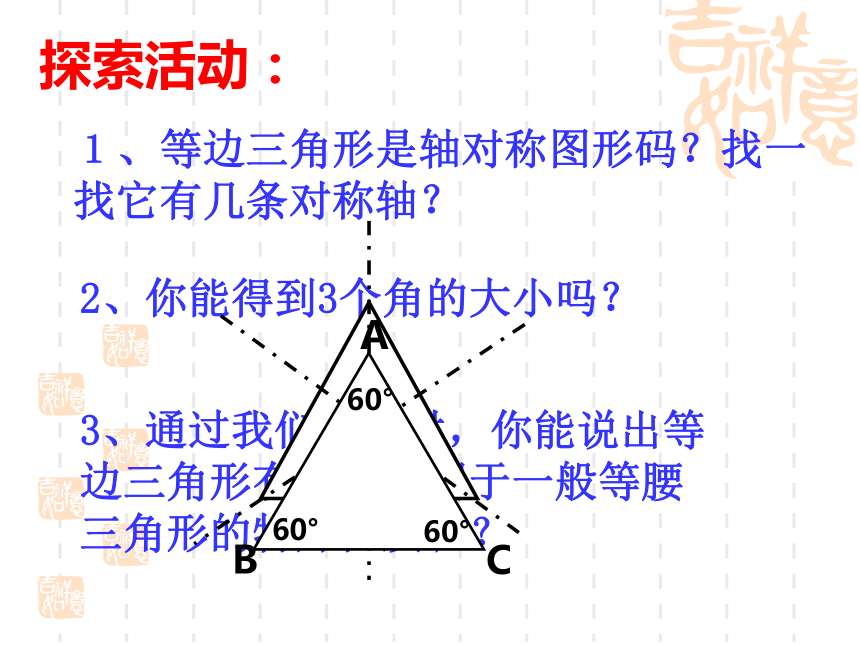
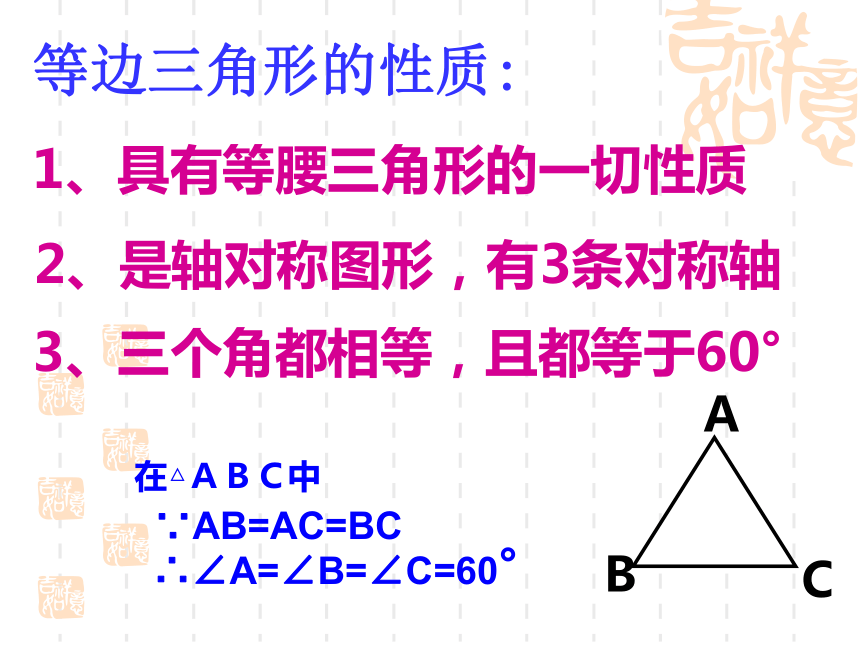
“三线合一” “等角对等边”思考 如果一个等腰三角形的腰和底边恰好相等,这样的三角形具有什么性质呢?你对它有哪些认识呢? 三边相等的三角形叫做等边三角形或正三角形.定义:探索活动:1、等边三角形是轴对称图形码?找一找它有几条对称轴?2、你能得到3个角的大小吗?3、通过我们的探讨,你能说出等边三角形有哪些不同于一般等腰三角形的特殊性质呢?等边三角形的性质:1、具有等腰三角形的一切性质2、是轴对称图形,有3条对称轴3、三个角都相等,且都等于60°1.如果三角形的三角都相等,那么该三角形为等边三角形吗? 思考:已知:在△ABC中,∠A= ∠B= ∠C求证:△ABC为等边三角形证明:∵∠A= ∠B
∴AC=BC
同理 AB=AC
∴AB=AC=BC
∴△ABC为等边三角形
2.如果等腰三角形的一角为600,那么该三角形为等边三角形吗? 设等腰三角形ABC中,AB=AC证明:∵ AB=AC ∠A= 60°
∴∠B=∠C= 60°
∴ ∠A=∠B=∠C
∴ △ABC是等边三角形如果∠B或∠C为60°,也能得到同样的结论吗?等边三角形的判定方法:1、等边三角形的定义2、三个角都相等的三角形是等边三角形3、有一个角是60°的等腰三角形是等边三角形小试牛刀1、如图,在等边三角形ABC中,BD、CE是两条中线。请你说出 ∠1、 ∠2、 ∠3、 ∠4的度数。ABCDE1234解:∵BD 、CE是等边三角形的中线
∴ BD是∠ABD的平分线
CE是AB边上的高
∴∠ABD=?∠ABC= 30°
∠BEC= 90°
∴∠1= 180°-∠ABD-∠BEC
= 180°- 30°- 90°
= 60°
∴∠2=∠1= 60°∠3=∠4= 180°- ∠1= 120°2、如图,△ABC是等边三角形,DE∥BC.分别交AB,AC于点D.求证:△ADE是等边三角形 小试牛刀证明:BCDEA∵△ABC是等边三角形∴∠A=∠B=∠C
∵DE∥BC
∴∠ADE=∠B
∠AED=∠C
∴∠A=∠ADE∠AED
∴△ADE是等边三角形3、如图,AB=AC,∠BAC=120°,AD⊥AB,AE⊥AC,△AED是等边三角形吗?为什么?解:∵AB=AC,∠BAC=120°∴ ∠B= ∠C=30°
∵ AD⊥AB,AE⊥AC∴ ∠BAD= ∠CAE= 90°
∴ ∠ADE= ∠AED= 60°
∴ ∠EAD= ∠ADE= ∠AED= 60°
∴ △AED是等边三角形动手试试看4、用不同的分割方法,将一个等边三角形分割成四个等腰三角形(注明角度)分割如图所示: 5、如图, △ABC和△CDE都是等边三角形,且点A、C、E在一直线上,度量并比较AD与BE的大小,能得到什么结论?说明理由.A小结:1、等边三角形的性质:(1)、具有等腰三角形的一切性质
(2)、是轴对称图形,有3条对称轴
(3)、三个角都相等,且都等于60°2、等边三角形的判定方法:(1)、等边三角形的定义
(2)、三个角都相等的三角形是等边三角形
(3)、有一个角是60°的等腰三角形是等边三角形
“等边对等角”
“三线合一” “等角对等边”思考 如果一个等腰三角形的腰和底边恰好相等,这样的三角形具有什么性质呢?你对它有哪些认识呢? 三边相等的三角形叫做等边三角形或正三角形.定义:探索活动:1、等边三角形是轴对称图形码?找一找它有几条对称轴?2、你能得到3个角的大小吗?3、通过我们的探讨,你能说出等边三角形有哪些不同于一般等腰三角形的特殊性质呢?等边三角形的性质:1、具有等腰三角形的一切性质2、是轴对称图形,有3条对称轴3、三个角都相等,且都等于60°1.如果三角形的三角都相等,那么该三角形为等边三角形吗? 思考:已知:在△ABC中,∠A= ∠B= ∠C求证:△ABC为等边三角形证明:∵∠A= ∠B
∴AC=BC
同理 AB=AC
∴AB=AC=BC
∴△ABC为等边三角形
2.如果等腰三角形的一角为600,那么该三角形为等边三角形吗? 设等腰三角形ABC中,AB=AC证明:∵ AB=AC ∠A= 60°
∴∠B=∠C= 60°
∴ ∠A=∠B=∠C
∴ △ABC是等边三角形如果∠B或∠C为60°,也能得到同样的结论吗?等边三角形的判定方法:1、等边三角形的定义2、三个角都相等的三角形是等边三角形3、有一个角是60°的等腰三角形是等边三角形小试牛刀1、如图,在等边三角形ABC中,BD、CE是两条中线。请你说出 ∠1、 ∠2、 ∠3、 ∠4的度数。ABCDE1234解:∵BD 、CE是等边三角形的中线
∴ BD是∠ABD的平分线
CE是AB边上的高
∴∠ABD=?∠ABC= 30°
∠BEC= 90°
∴∠1= 180°-∠ABD-∠BEC
= 180°- 30°- 90°
= 60°
∴∠2=∠1= 60°∠3=∠4= 180°- ∠1= 120°2、如图,△ABC是等边三角形,DE∥BC.分别交AB,AC于点D.求证:△ADE是等边三角形 小试牛刀证明:BCDEA∵△ABC是等边三角形∴∠A=∠B=∠C
∵DE∥BC
∴∠ADE=∠B
∠AED=∠C
∴∠A=∠ADE∠AED
∴△ADE是等边三角形3、如图,AB=AC,∠BAC=120°,AD⊥AB,AE⊥AC,△AED是等边三角形吗?为什么?解:∵AB=AC,∠BAC=120°∴ ∠B= ∠C=30°
∵ AD⊥AB,AE⊥AC∴ ∠BAD= ∠CAE= 90°
∴ ∠ADE= ∠AED= 60°
∴ ∠EAD= ∠ADE= ∠AED= 60°
∴ △AED是等边三角形动手试试看4、用不同的分割方法,将一个等边三角形分割成四个等腰三角形(注明角度)分割如图所示: 5、如图, △ABC和△CDE都是等边三角形,且点A、C、E在一直线上,度量并比较AD与BE的大小,能得到什么结论?说明理由.A小结:1、等边三角形的性质:(1)、具有等腰三角形的一切性质
(2)、是轴对称图形,有3条对称轴
(3)、三个角都相等,且都等于60°2、等边三角形的判定方法:(1)、等边三角形的定义
(2)、三个角都相等的三角形是等边三角形
(3)、有一个角是60°的等腰三角形是等边三角形
