13.3.2 等边三角形
文档属性
| 名称 | 13.3.2 等边三角形 |  | |
| 格式 | zip | ||
| 文件大小 | 211.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-20 10:27:09 | ||
图片预览




文档简介
课件16张PPT。13.3.2等边三角形(2) (1) 等边三角形的性质.
回忆1.具有等腰三角形的一切性质
2.等边三角形是轴对称图形,有三条对称轴.
3.等边三角形的内角都相等,且等于60 °(2) 等边三角形的判定:1.三边相等的三角形是等边三角形.
2.三个内角都相等的三角形是等边三角形.
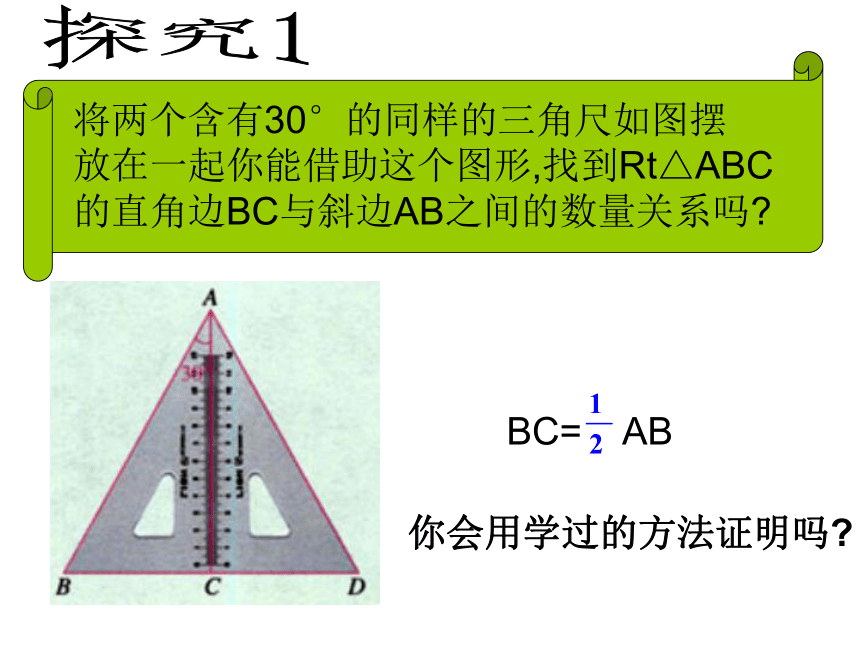
3.有一个内角等于60 °的等腰三角形是等边三角形.探究1你会用学过的方法证明吗?将两个含有30°的同样的三角尺如图摆
放在一起你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
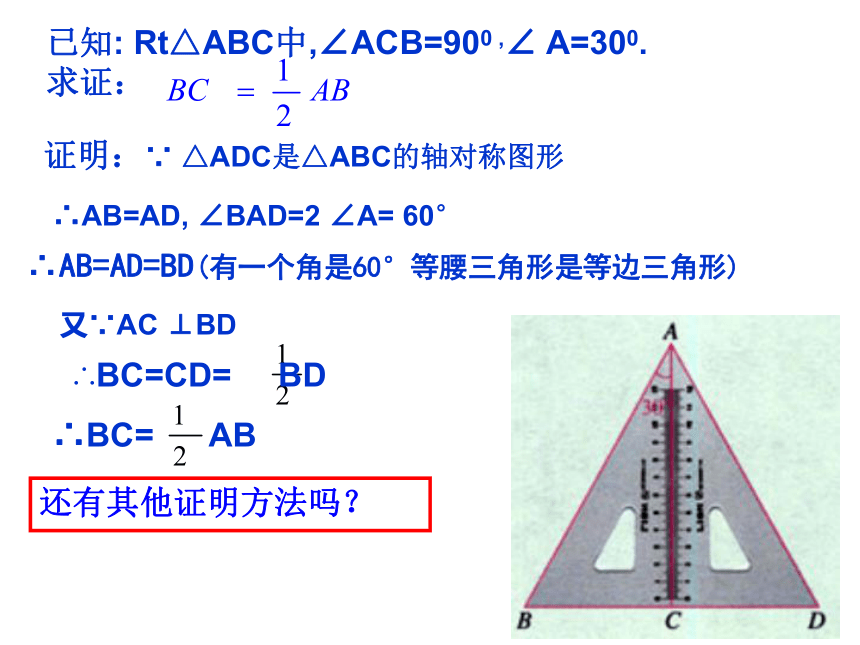
证明:∵ △ADC是△ABC的轴对称图形∴AB=AD=BD(有一个角是60°等腰三角形是等边三角形)还有其他证明方法吗?∴AB=AD, ∠BAD=2 ∠A= 60°又∵AC ⊥BD证明:在斜边AB上截取BD=BC,连接CD∴△ACD是等腰三角形在△ABC中,∠ACB= 90°,∠ A= 30°∴AD=CD=BD=BC你能用一句话来描述你的结论吗?300∴ ∠B= 60°又∵BD=BC∴△BCD是等边三角形∴ ∠BDC= 60°∴ ∠ACD= 30°∴ ∠A= ∠ACD这是一个判定两条线段成倍半关系的根据之一.定理:在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.在△ABC中,∵∠ACB=900,∠A=300.
∴BC= AB.
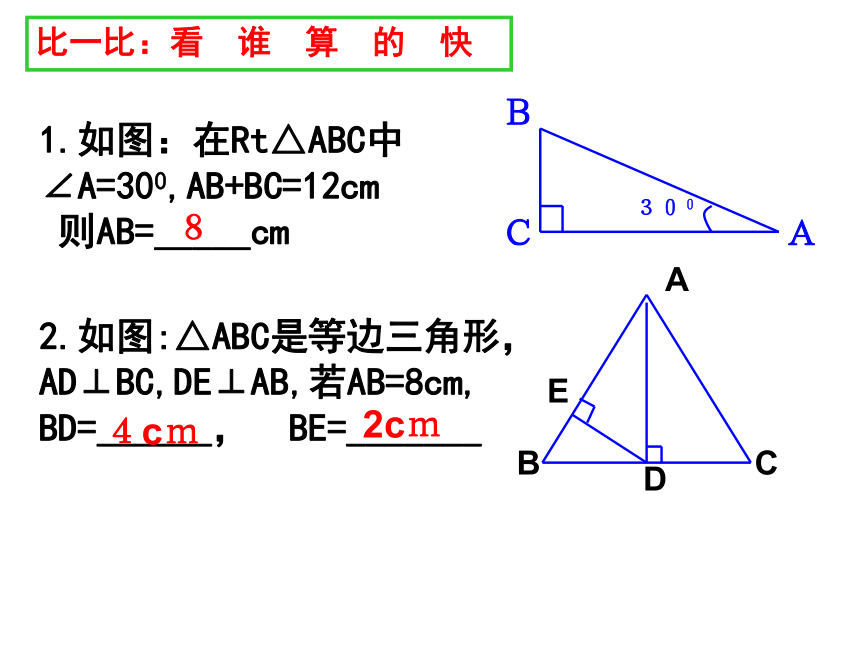
(在直角三角形中, 300角所对的直角边等于斜边的一半).应用归纳比一比:看 谁 算 的 快1.如图:在Rt△ABC中
∠A=300,AB+BC=12cm
则AB=_____cm82.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm,
BD=___, BE=_______4cm 2cm解:∵DE⊥AC, ∠A=30°
∴ AD = 2DE
(在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半)
同理可得: AB = 2BC,
∵ AB=7.4m∴BC=1/2 ×7.4=3.7m
又 ∵ D是AB的中点
∴ AD=1/2 AB=3.7m
∴DE=1/2 AD=1/2 ×3.7=1.85m
答:立柱BC的长是3.7m,DE的长是1.85m. 例1.下图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、 DE垂直于横梁AC,AB=7.4m,∠A=30°立柱BC 、 DE要多长?解:∵∠DAC是△ABC的外角∴∠DAC=∠ABC+∠ACB∵ ∠ABC=∠ACB=15°∴∠DAC=30°∵ CD是腰AB上的高例2. 如图在△ ABC中, AB=AC=2a, ∠ABC=∠ACB=150,CD是腰AB上
的高,求CD的长┏DCBA反过来怎么样——逆向思维命题:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.
是真命题吗?如果是,请你证明它.ABC已知:如图,在△ABC中,∠ACB=900,BC= AB.
求证:∠A=300.反过来怎么样——逆向思维在△ABD中,∵∠ACB=900(已知),
∴AB=AD(线段垂直平分线上的点到线段两端的距离相等).
又∵BC=AB/2(已知),
BC=BD/2(作图),
∴AB=BD(等量代换).
∴AB=BD=AD(等式性质).
∴△ABD是等边三角形(等边三角形定义).
∴∠B=600(等边三角形定义).
∴∠A=300(直角三角形两锐角互余).300ABC证明:如图, 延长BC至D,使CD=BC,连接AD.几何的三种语言′这是一个通过线段之间的关系来判定一个角的具体度数(300)的根据之一.定理:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.在△ABC中
∵∠ACB=900,BC=AB/2(已知),
∴∠A=300(在直角三角形中,如果一条直角边等于斜边的一半,那么它所对的锐角等于300).应用:1.如图,△ABC是等边三角形,P、Q分别是AC、BC上的点,且AP=CQ,AQ与BP交于点M。求∠BMQ的度数。考考你MCABPQ2.已知:如图,在等边△ABC中,D、E分别为BC、AC上的点,且AE=CD,连结AD、BE交于点P,作BQ⊥AD于Q,
求证:
(1)∠APE=60°(2)BP=2PQ.ABCEQ DP回味无穷等边三角形的判定:
1.有三边相等的三角形是等边三角形.
2.三个角都相等的三角形是等边三角形.
3.有一个角是600的等腰三角形是等边三角形.
特殊的直角三角形的性质:
1.在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.
2.在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.等边三角形的性质:
三边相等,三个角都是600,”三线合一”,三条对称轴.作业82页9题 83页15题
回忆1.具有等腰三角形的一切性质
2.等边三角形是轴对称图形,有三条对称轴.
3.等边三角形的内角都相等,且等于60 °(2) 等边三角形的判定:1.三边相等的三角形是等边三角形.
2.三个内角都相等的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.探究1你会用学过的方法证明吗?将两个含有30°的同样的三角尺如图摆
放在一起你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
证明:∵ △ADC是△ABC的轴对称图形∴AB=AD=BD(有一个角是60°等腰三角形是等边三角形)还有其他证明方法吗?∴AB=AD, ∠BAD=2 ∠A= 60°又∵AC ⊥BD证明:在斜边AB上截取BD=BC,连接CD∴△ACD是等腰三角形在△ABC中,∠ACB= 90°,∠ A= 30°∴AD=CD=BD=BC你能用一句话来描述你的结论吗?300∴ ∠B= 60°又∵BD=BC∴△BCD是等边三角形∴ ∠BDC= 60°∴ ∠ACD= 30°∴ ∠A= ∠ACD这是一个判定两条线段成倍半关系的根据之一.定理:在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.在△ABC中,∵∠ACB=900,∠A=300.
∴BC= AB.
(在直角三角形中, 300角所对的直角边等于斜边的一半).应用归纳比一比:看 谁 算 的 快1.如图:在Rt△ABC中
∠A=300,AB+BC=12cm
则AB=_____cm82.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm,
BD=___, BE=_______4cm 2cm解:∵DE⊥AC, ∠A=30°
∴ AD = 2DE
(在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半)
同理可得: AB = 2BC,
∵ AB=7.4m∴BC=1/2 ×7.4=3.7m
又 ∵ D是AB的中点
∴ AD=1/2 AB=3.7m
∴DE=1/2 AD=1/2 ×3.7=1.85m
答:立柱BC的长是3.7m,DE的长是1.85m. 例1.下图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、 DE垂直于横梁AC,AB=7.4m,∠A=30°立柱BC 、 DE要多长?解:∵∠DAC是△ABC的外角∴∠DAC=∠ABC+∠ACB∵ ∠ABC=∠ACB=15°∴∠DAC=30°∵ CD是腰AB上的高例2. 如图在△ ABC中, AB=AC=2a, ∠ABC=∠ACB=150,CD是腰AB上
的高,求CD的长┏DCBA反过来怎么样——逆向思维命题:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.
是真命题吗?如果是,请你证明它.ABC已知:如图,在△ABC中,∠ACB=900,BC= AB.
求证:∠A=300.反过来怎么样——逆向思维在△ABD中,∵∠ACB=900(已知),
∴AB=AD(线段垂直平分线上的点到线段两端的距离相等).
又∵BC=AB/2(已知),
BC=BD/2(作图),
∴AB=BD(等量代换).
∴AB=BD=AD(等式性质).
∴△ABD是等边三角形(等边三角形定义).
∴∠B=600(等边三角形定义).
∴∠A=300(直角三角形两锐角互余).300ABC证明:如图, 延长BC至D,使CD=BC,连接AD.几何的三种语言′这是一个通过线段之间的关系来判定一个角的具体度数(300)的根据之一.定理:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.在△ABC中
∵∠ACB=900,BC=AB/2(已知),
∴∠A=300(在直角三角形中,如果一条直角边等于斜边的一半,那么它所对的锐角等于300).应用:1.如图,△ABC是等边三角形,P、Q分别是AC、BC上的点,且AP=CQ,AQ与BP交于点M。求∠BMQ的度数。考考你MCABPQ2.已知:如图,在等边△ABC中,D、E分别为BC、AC上的点,且AE=CD,连结AD、BE交于点P,作BQ⊥AD于Q,
求证:
(1)∠APE=60°(2)BP=2PQ.ABCEQ DP回味无穷等边三角形的判定:
1.有三边相等的三角形是等边三角形.
2.三个角都相等的三角形是等边三角形.
3.有一个角是600的等腰三角形是等边三角形.
特殊的直角三角形的性质:
1.在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.
2.在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.等边三角形的性质:
三边相等,三个角都是600,”三线合一”,三条对称轴.作业82页9题 83页15题
