双曲线

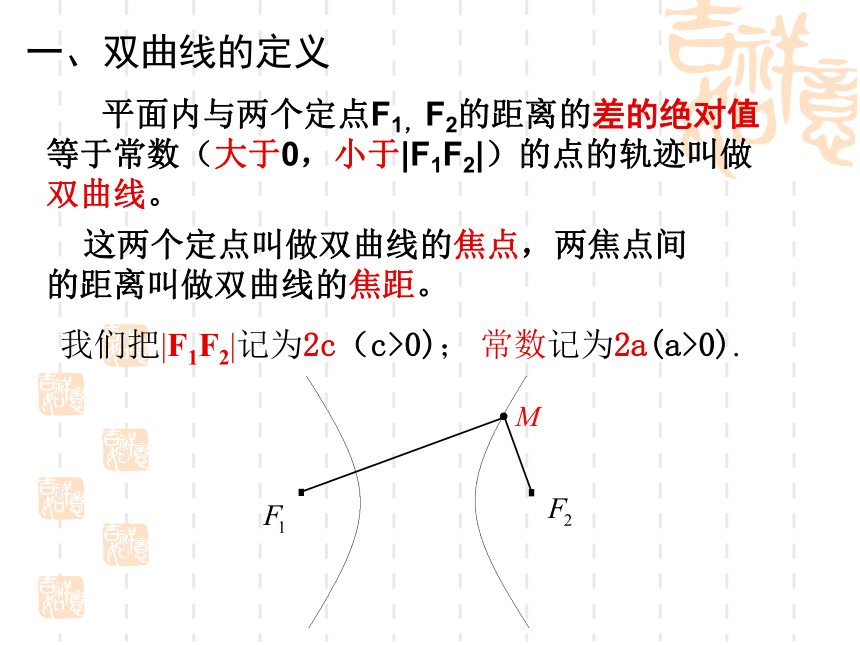
课件19张PPT。问题1：奎屯市现准备在离高级中学1公里的地方建立一海洋公园，公园可以建的所有位置构成一个什么图形？问题2：假设高级中学与三中的距离为1公里，海洋公园要求建在到高级中学与到三中的距离相等处，公园可以建的所有位置构成一个什么图形？问题3：假设高级中学与三中的距离为1公里，推广站要求建在到高级中学与到三中的距离的和为2公里处，公园可以建的所有位置构成一个什么图形？问题4：假设高级中学与三中的距离为1公里，推广站要求建在到高级中学与到三中的距离的差为0.2公里处，公园可以建的所有位置构成一个什么图形？ 平面内与两定点F1，F2的“距离的差”等于常数的点的轨迹是什么？共同探究动画演示②若2a=0时此时轨迹为线段F1F2的垂直平分线F1F2记| F1F2|=2c，常数记为2a。①若2a<2c，且不等于0时此时轨迹为一支曲线2.3.1 双曲线及其标准方程 这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距。 我们把|F1F2|记为2c（c>0)； 常数记为2a(a>0).一、双曲线的定义二、双曲线标准方程的推导① 建系② 设点③ 列式将上述方程化为： 移项两边平方后整理得： 两边再平方后整理得： 设 代入上式整理得： ④化简这个方程叫做双曲线的标准方程 ，它所表示的双曲线的焦点在x轴上，焦点是 F1(-c，0)，F2(c，0).其中c2=a2+b2.整理成：思考其中c2=a2+b2. 这个方程也叫做双曲线的标准方程 ，它所表示的双曲线的焦点在y轴上，焦点是 F1(0，-c)，F2(0，c).三.双曲线两种标准方程的比较① 方程用“－”号连接，右边为1。焦点符号正，a随正值走练一练判断下列方程表示双曲线的焦点位置并求出 及焦点坐标。答案：解：因此，双曲线的标准方程为例1、已知双曲线的焦点 F1(-5,0), F2(5,0)，双曲线上一点P到焦点的距离差的绝对值等于8，求双曲线的标准方程。若|PF1|-|PF2|=8呢？所以2c=10，2a=8。即a=4，c=5那么b2=c2-a2=25-16=9根据已知条件，|F1F2|=10. ||PF1|-|PF2||=8，
焦点在x轴上。变式：问题4：假高级中学与三中的距离为1公里，海洋公园要求建在到高级中学与到三中的距离的差为0.2公里处，公园可以建的所有位置构成一个什么图形？能求出轨迹其方程吗？ 使A、B两点在x轴上，并且点O与线段AB的中点重合解: 设高级中学在A地，三中在B地；公园建在P处,可知P到A地比到B地远0.2公里.因为0.2<|AB|,所以公园P的轨迹是以A、B为焦点的双曲线在靠近B处的一支上.如图所示，建立直角坐标系xOy,设公园P的坐标为(x,y)，则即 2a=0.2，a=0.1因此公园可建位置的轨迹方程为课后思考①若2a=2c时，轨迹是什么？②若2a>2c时，轨迹是什么？记| F1F2|=2c，常数记为2a。归纳小结双曲线的定义双曲线的标准方程标准方程的应用布置作业课本55页练习3
61页习题2.3 A组1、2题。F（±c，0）F（±c，0）a>0，b>0，但a不一定大于b，c2=a2+b2a>b>0，a2=b2+c2双曲线与椭圆之间的区别与联系||MF1|－|MF2||=2a |MF1|+|MF2|=2a F（0，±c）F（0，±c）分母大符号正方程焦点a.b.c 的关系图象定义| |MF1|-|MF2| | =2a（０ < 2a<|F1F2|）F(0, ± c)焦点在X轴上焦点在Y轴上F ( ±c, 0)焦点位置小结：双曲线两种标准方程焦点符号正
a 随正值走= = 我！谢谢Bye Bye!