华师大版数学九年级上册 24.2 直角三角形的性质 教案
文档属性
| 名称 | 华师大版数学九年级上册 24.2 直角三角形的性质 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 113.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-27 00:00:00 | ||
图片预览


文档简介
24.2直角三角形的性质
【教学目标】
依据课程标准,本节课的学习目标是:
知识与技能:
1、直角三角形斜边上的中线等于斜边的一半
2、能利用直角三角形的性质定理进行有关的计算和证明
过程与方法
经历“计算——探索——发现——猜想——证明”的过程,引导学生体会合情推理与演绎推理的相互依赖和相互补充。
情感态度与价值观通过“计算——探索—发现—猜想—证明”的过程体验数学活动中的探索与创新,感受数学的严谨性,激发学生的好奇心和求知欲,培养学习的自信心。
【教学重难点】
教学重点:
1、掌握直角三角形性质:
2、能利用直角三角形的性质定理进行有关的计算和证明
教学难点:
能利用直角三角形的性质定理进行有关的计算和证明
【教学方法与策略】
本节主要想采用“启发探究式”教学方法,围绕本节课所学知识,设计问题,激发学生积极思考,在教学中以启发学生进行探究的形式展开,引导学生自主学习与合作交流,不断丰富数学活动的经验,增强学生学习过程中的反思意识,通过猜想验证、归纳总结,使学生积极参与教学过程,进一步培养学生提出问题、分析问题、解决问题的能力。
【教学环境和资源的准备】
ppt课件、电子白板、实物展示仪
【教学过程】
(一)新课导入
1、花开的声音:
让学生朗诵证明性质3时要用到的相关定义、定理。
2、直角三角形是一类特殊的三角形,除了具备三角形的性质外,还具备哪些性质 让学生从角和边多方面回答。
(二)新课讲授
一、引练(设计意图:引导学生回顾平行四边形,矩形性质及判定)
1.在平行四边形ABCD中,如果∠A=90°,那么四边形ABCD是----------
2.在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB = 60°, AC=10,则AB = ----------
3、课堂活动:
(1)画一个直角三角形
(2)量量斜边AB的长度
(3)找到斜边的中点,用字母D表示
(4)画出斜边的中线
(5)量量斜边上的中线的长度
(设计意图:通过学生动手操作感受到直角三角形斜边中线等于斜边一半,然后通过集合画板展示任一直角三角形都由此结论)
二.实验探究,探索新知(设计意图:通过演绎推理证明此结论)
(通过感受直角三角形的直角边和中线之间的关系是从矩形对角线而来的,为下一步证明性质定理做好铺垫,同时也启发了学生从实践中发现一些客观存在的规律。
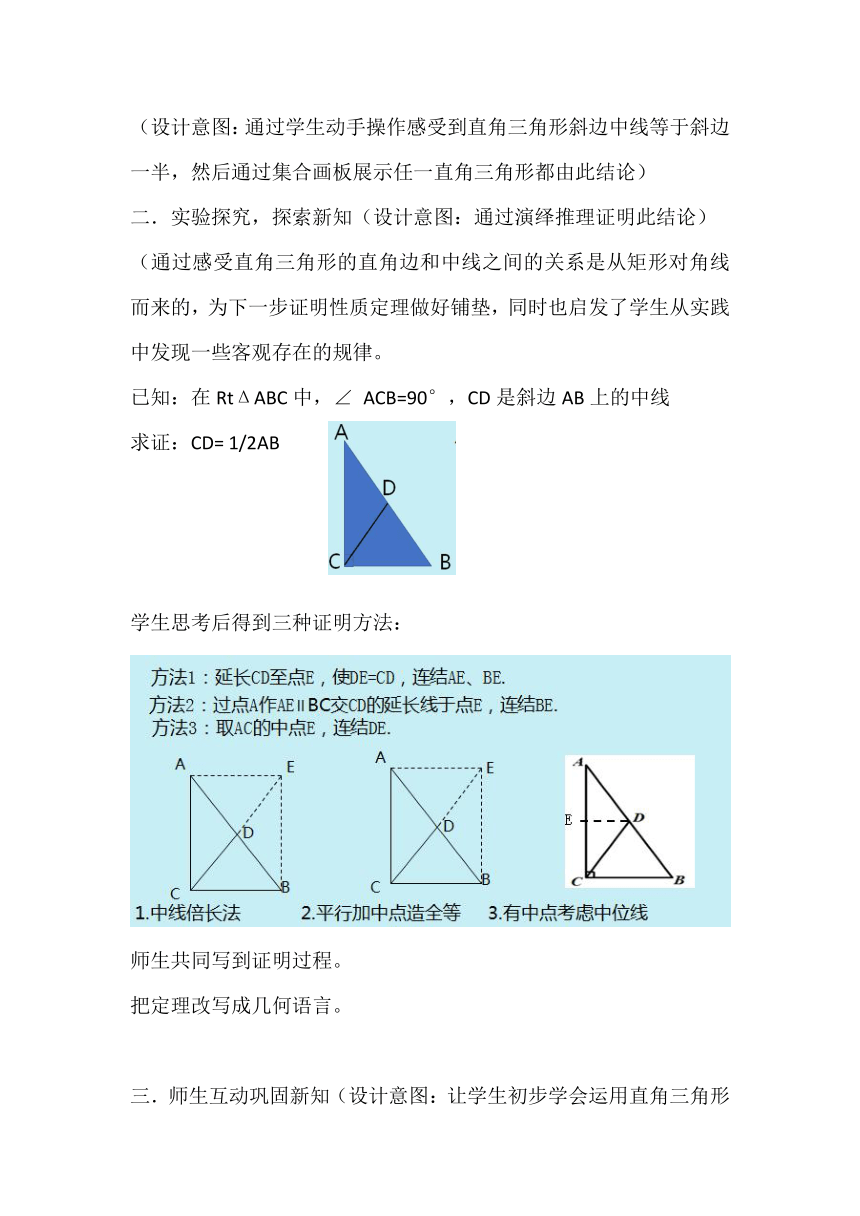
已知:在RtΔABC中,∠ ACB=90°,CD是斜边AB上的中线
求证:CD= 1/2AB
学生思考后得到三种证明方法:
师生共同写到证明过程。
把定理改写成几何语言。
三.师生互动巩固新知(设计意图:让学生初步学会运用直角三角形性质3解决与直角三角形有关的问题,加深对性质3的理解。)
1、如图Rt⊿ABC中,∠ACB=90°,点D,F分别是AC,BC边上的中点,点E是AB边上的中点,如果CE=3,则DF=_
2、 如图:在RtΔABC中,CD是斜边AB上的中线,已知∠DCA=20°,则∠ A =_,∠B=____。
四.迁移新知,能力拓展(设计意图:让学生经历发现探索过程,还需要给以证明)五.知识应用,拓展提高(设计意图:进一步巩固直角三角形性质3和性质4)
已知:在RtΔABC中,∠ACB= 90°, ∠A= 30°
求证:BC= AB
师生共同完成证明过程。得到:性质4:30°角所对的直角边等于斜边的一半。
五、课堂练习
六.拓展提高(设计意图:针对能力强的学生进行课余探索而设计,目的是让不同层次的学生都有收获)
七、课堂小结,自主评价
1、通过本节课的学习你学到了直角三角形的哪些知识?
2、通过例题和习题的计算和证明给你带来了哪些收获和体会?
3、在直角三角形的性质定理的应用过程中应该注意哪些问题?
八.作业:
104页1.2.3
九.板书设计
性质3直角三角形斜边上的中线等于斜边的一半;
性质4直角三角形中,如果有一个锐角等于30度,那么它所对的直角边等于斜边的一半。
【教学目标】
依据课程标准,本节课的学习目标是:
知识与技能:
1、直角三角形斜边上的中线等于斜边的一半
2、能利用直角三角形的性质定理进行有关的计算和证明
过程与方法
经历“计算——探索——发现——猜想——证明”的过程,引导学生体会合情推理与演绎推理的相互依赖和相互补充。
情感态度与价值观通过“计算——探索—发现—猜想—证明”的过程体验数学活动中的探索与创新,感受数学的严谨性,激发学生的好奇心和求知欲,培养学习的自信心。
【教学重难点】
教学重点:
1、掌握直角三角形性质:
2、能利用直角三角形的性质定理进行有关的计算和证明
教学难点:
能利用直角三角形的性质定理进行有关的计算和证明
【教学方法与策略】
本节主要想采用“启发探究式”教学方法,围绕本节课所学知识,设计问题,激发学生积极思考,在教学中以启发学生进行探究的形式展开,引导学生自主学习与合作交流,不断丰富数学活动的经验,增强学生学习过程中的反思意识,通过猜想验证、归纳总结,使学生积极参与教学过程,进一步培养学生提出问题、分析问题、解决问题的能力。
【教学环境和资源的准备】
ppt课件、电子白板、实物展示仪
【教学过程】
(一)新课导入
1、花开的声音:
让学生朗诵证明性质3时要用到的相关定义、定理。
2、直角三角形是一类特殊的三角形,除了具备三角形的性质外,还具备哪些性质 让学生从角和边多方面回答。
(二)新课讲授
一、引练(设计意图:引导学生回顾平行四边形,矩形性质及判定)
1.在平行四边形ABCD中,如果∠A=90°,那么四边形ABCD是----------
2.在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB = 60°, AC=10,则AB = ----------
3、课堂活动:
(1)画一个直角三角形
(2)量量斜边AB的长度
(3)找到斜边的中点,用字母D表示
(4)画出斜边的中线
(5)量量斜边上的中线的长度
(设计意图:通过学生动手操作感受到直角三角形斜边中线等于斜边一半,然后通过集合画板展示任一直角三角形都由此结论)
二.实验探究,探索新知(设计意图:通过演绎推理证明此结论)
(通过感受直角三角形的直角边和中线之间的关系是从矩形对角线而来的,为下一步证明性质定理做好铺垫,同时也启发了学生从实践中发现一些客观存在的规律。
已知:在RtΔABC中,∠ ACB=90°,CD是斜边AB上的中线
求证:CD= 1/2AB
学生思考后得到三种证明方法:
师生共同写到证明过程。
把定理改写成几何语言。
三.师生互动巩固新知(设计意图:让学生初步学会运用直角三角形性质3解决与直角三角形有关的问题,加深对性质3的理解。)
1、如图Rt⊿ABC中,∠ACB=90°,点D,F分别是AC,BC边上的中点,点E是AB边上的中点,如果CE=3,则DF=_
2、 如图:在RtΔABC中,CD是斜边AB上的中线,已知∠DCA=20°,则∠ A =_,∠B=____。
四.迁移新知,能力拓展(设计意图:让学生经历发现探索过程,还需要给以证明)五.知识应用,拓展提高(设计意图:进一步巩固直角三角形性质3和性质4)
已知:在RtΔABC中,∠ACB= 90°, ∠A= 30°
求证:BC= AB
师生共同完成证明过程。得到:性质4:30°角所对的直角边等于斜边的一半。
五、课堂练习
六.拓展提高(设计意图:针对能力强的学生进行课余探索而设计,目的是让不同层次的学生都有收获)
七、课堂小结,自主评价
1、通过本节课的学习你学到了直角三角形的哪些知识?
2、通过例题和习题的计算和证明给你带来了哪些收获和体会?
3、在直角三角形的性质定理的应用过程中应该注意哪些问题?
八.作业:
104页1.2.3
九.板书设计
性质3直角三角形斜边上的中线等于斜边的一半;
性质4直角三角形中,如果有一个锐角等于30度,那么它所对的直角边等于斜边的一半。
