2.1有理数 课件（15张PPT）

(共15张PPT)
第二章 有理数
§2.1有理数
糖球儿
知识点1 正数、负数、零
1. 一般地，对于具有相反意义的量，我们把其中一种意义的量规定为正，用正数表示，把与它意义相反的量规定为负，用负数表示。
2.意义：
比0大的数是正数，
在正数的前面加上“-”号，就得到负数，负数都比0小
0既不是正数也不是负数
eg:规定收入为正，收入500元，记作+500元（或500元）
支出30元，记作-30元
拓展
（1）正数前面的正号可以省略，且注意，带负号的不一定是负数
（2）0除了表示一个也没有外，还可以表示其他意义。他是正数和负数的分界点
（3）相反意义的量都是成对出现的，单独一个量不能称其是相反意义的量
（4）具有相反意义的量必须是同类量
（5）用正、负数表示具有相反意义的量时，一定要说明数量和单位。
eg：填空
（1）收入800元记作800元，那么-90元表示___________
（2）向南走-200米表示____________
支出90元
向西走200米
知识点2 有理数
1.整数:正整数、零、负整数统称为整数
分数：正分数、负分数统称为分数
有理数：整数和分数统称为有理数
2.拓展
（1）因为有限小数和无限循环小数可以化成分数，所以有限小数和无限循环小数是有理数。
（2）无限不循环小数不能化成分数，故不是分数，也不是有理数，如：π，0.101001000100001······(每两个1中间多一个0)不是有理数
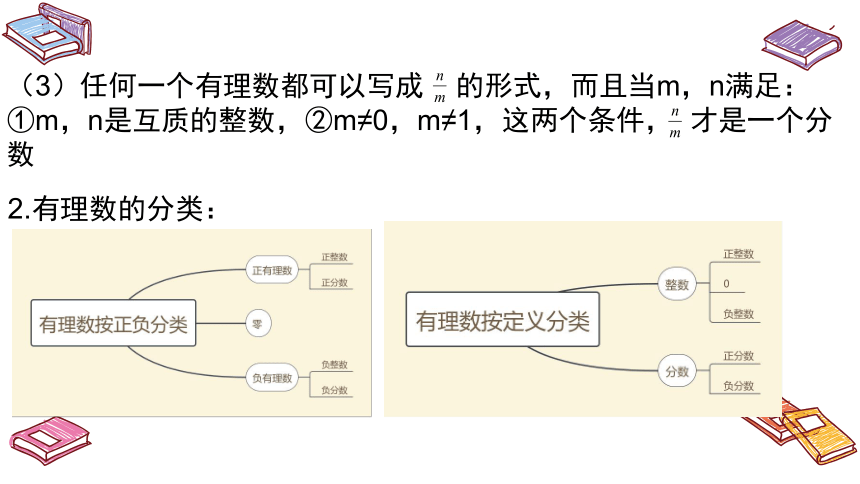
（3）任何一个有理数都可以写成 的形式，而且当m，n满足：
①m，n是互质的整数，②m≠0，m≠1，这两个条件， 才是一个分数
2.有理数的分类：
eg:下列分类中，错误的是（ ）
A.有理数：{负有理数 B.正整数：{奇数
非负有理数 偶数
C.整数：{正整数 D.自然数：{0
非正整数 正整数
B
解析：对于A，非负有理数包括0和正有理数，故A正确
对于B，0是偶数也是整数，但不是正数，即0不是正整数
3.拓展：
（1）正数和零统称为非负数；
负数和零统称为非正数；
正整数和零统称为非负整数，又叫自然数；
负整数和零统称为非正整数。
（2）注意：“正”和“整”的区别
“正”是相对于“负”而言的
“整”是相对于“分”而言的
eg：下列各数哪些数是有理数？哪些是分数？
30 -3.5 0 π -3 - 3 -40
有理数:
分数：
eg：分别写出符合条件的一个有理数
（1）既是正数又是分数的一个数：
（2）既是负数又是整数的一个数：
-4（答案不唯一）
知识点3 数集
1.数集：把一些数放在一起，就组成一个数的集合，简称数集。
2.有理数集：所有有理数组成的集合叫有理数集
整数集：所有整数组成的集合叫整数集（正整数、0、 负整数）
负数集：所有负数组成的集合叫负数集
非负数集：所有正整数与零组成的集合叫非负数集
3.拓展：
（1）数集可以用大括号表示，也可以用圆圈表示
（2）一个数集不能有重复的数（互异性）
（3）集合的特性：无序性、确定性、无序性
（4）一个数集内的数有无限多个，我们不能全部写出时， 用”······”
表示
把下面各数填在相应的大括号内
（1）正整数集{ ···}
（2）负分数集{ ···}
（3）正数集{ ···}
（4）负数集{ ···}
（5）非负整数集{ ···}
6，+67,2000
6，+67,2000，0
eg：A、B、C是三个数集，每个数集中包含的数都写在各自的大括号内，填空
A={-2，-3，-8，6，9} B={-2，-5，2，6，10}
C={-4,-2,-8-10,13}
A
B
C
-3,9
6
-8
-2
-5,2,10
-4，-10,13
eg :长江某观测站的水位达12米时警戒水位，如果超过警戒水位1米记作+1米，那么低于警戒水位0.3米记作______
日期 7.1 7.2 7.3 7.4 7.5 ···
水位（米） -0.8 0 0.38 0.5 0.96 ···
（1）哪天的水位最高？最高水位是多少？
（2）哪天水位最低？最低水位是多少？
-0.3米
7.5日水位最高，最高水位是12+0.96=12.96米
7.1日水位最低，最低水位是12-0.8=11.2米
THANK YOU
谢谢聆听