13.2.1等边三角形1学案
文档属性
| 名称 | 13.2.1等边三角形1学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 22.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-20 00:00:00 | ||
图片预览

文档简介
八年级(上) 数学 学案
13.2.2等边三角形(1)
班别: 姓名: 主备人:
教研组长审批: 教务处审批:
一、【学习目标】
①了解等边三角形是特殊的等腰三角形,等边三角形是轴对称图形.
②会阐述、推证等边三角形的性质和判定方法.
【学习重点】等边三角形的性质和判定定理;
【学习难点】等边三角形性质和判定的应用.
一、课前导学:(自学课本第79—80页,完成下列问题)
1、在△ABC中,
若AB=AC,则 ;(填角的关系)
若∠B=∠C,则 。(填边的关系)
2、在△ABC中,若AB=AC,AD是BC边上的高,则有
∠____=∠_BAD__; BD=____
依据是
3、等腰三角形判定方法: ;
简写成:“ ”;
4、等边三角形是 的特殊的等腰三角形。
二、探究新知
(一)三条边都相等的三角形叫做 三角形
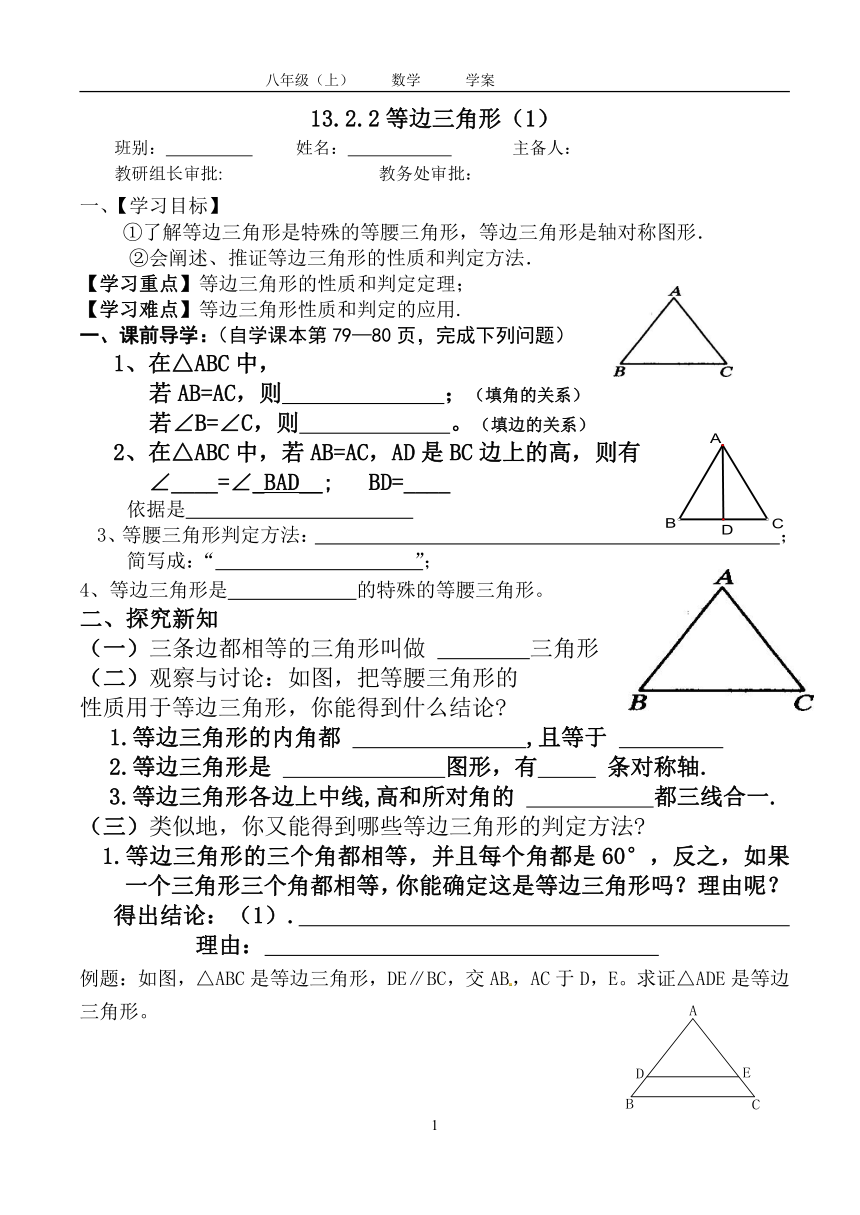
(二)观察与讨论:如图,把等腰三角形的
性质用于等边三角形,你能得到什么结论
1.等边三角形的内角都 ,且等于
2.等边三角形是 图形,有 条对称轴.
3.等边三角形各边上中线,高和所对角的 都三线合一.
(三)类似地,你又能得到哪些等边三角形的判定方法
1.等边三角形的三个角都相等,并且每个角都是60°,反之,如果一个三角形三个角都相等,你能确定这是等边三角形吗?理由呢?
得出结论:(1).
理由:
例题:如图,△ABC是等边三角形,DE∥BC,交AB,AC于D,E。求证△ADE是等边三角形。
变式:△ABC是等边三角形,以下三种方法分别得到的△ADE都是等边三角形吗?为什么
①在边AB、AC上分别截取AD=AE.
②作∠ADE=60°,D、E分别在边AB、AC上.
③过边AB上D点作DE∥BC,交边AC于E点。
等边三角形的判定:
三、巩固与应用
1.等边三角形的三条边都 ,三个角 。
2. 如下图,△ABC为等边三角形,BD为高,CE为角平分线,BD与CE相交于点O,则,∠ABD=__,∠BOC=__.
3、下列四个说法中,不正确的有( )
(1)三条边都相等的三角形是等边三角形。
(2)有两个角等于60°的三角形是等边三角形。
(3)有一个是60°的等腰三角形是等边三角形。
(4)等腰三角形是等边三角形。
(A)0个(B)1个(C)2个(D)3个
4、等边三角形的对称轴有( ) (A)1条(B)2条(C)3条(D)4条
四.能力提升
1.已知:如图,P、Q是△ABC的边BC上的两点,,并且PB=PQ=QC=AP=AQ.求∠BAC的大小.
2.如图,△ABD,△AEC都是等边三角形,求证BE=DC。
四、小结:1、知识要点:
2、思想方法:
五、作业:1、课本P80练习T1、2;
O
C
B
A
第2题
E
D
PAGE
2
13.2.2等边三角形(1)
班别: 姓名: 主备人:
教研组长审批: 教务处审批:
一、【学习目标】
①了解等边三角形是特殊的等腰三角形,等边三角形是轴对称图形.
②会阐述、推证等边三角形的性质和判定方法.
【学习重点】等边三角形的性质和判定定理;
【学习难点】等边三角形性质和判定的应用.
一、课前导学:(自学课本第79—80页,完成下列问题)
1、在△ABC中,
若AB=AC,则 ;(填角的关系)
若∠B=∠C,则 。(填边的关系)
2、在△ABC中,若AB=AC,AD是BC边上的高,则有
∠____=∠_BAD__; BD=____
依据是
3、等腰三角形判定方法: ;
简写成:“ ”;
4、等边三角形是 的特殊的等腰三角形。
二、探究新知
(一)三条边都相等的三角形叫做 三角形
(二)观察与讨论:如图,把等腰三角形的
性质用于等边三角形,你能得到什么结论
1.等边三角形的内角都 ,且等于
2.等边三角形是 图形,有 条对称轴.
3.等边三角形各边上中线,高和所对角的 都三线合一.
(三)类似地,你又能得到哪些等边三角形的判定方法
1.等边三角形的三个角都相等,并且每个角都是60°,反之,如果一个三角形三个角都相等,你能确定这是等边三角形吗?理由呢?
得出结论:(1).
理由:
例题:如图,△ABC是等边三角形,DE∥BC,交AB,AC于D,E。求证△ADE是等边三角形。
变式:△ABC是等边三角形,以下三种方法分别得到的△ADE都是等边三角形吗?为什么
①在边AB、AC上分别截取AD=AE.
②作∠ADE=60°,D、E分别在边AB、AC上.
③过边AB上D点作DE∥BC,交边AC于E点。
等边三角形的判定:
三、巩固与应用
1.等边三角形的三条边都 ,三个角 。
2. 如下图,△ABC为等边三角形,BD为高,CE为角平分线,BD与CE相交于点O,则,∠ABD=__,∠BOC=__.
3、下列四个说法中,不正确的有( )
(1)三条边都相等的三角形是等边三角形。
(2)有两个角等于60°的三角形是等边三角形。
(3)有一个是60°的等腰三角形是等边三角形。
(4)等腰三角形是等边三角形。
(A)0个(B)1个(C)2个(D)3个
4、等边三角形的对称轴有( ) (A)1条(B)2条(C)3条(D)4条
四.能力提升
1.已知:如图,P、Q是△ABC的边BC上的两点,,并且PB=PQ=QC=AP=AQ.求∠BAC的大小.
2.如图,△ABD,△AEC都是等边三角形,求证BE=DC。
四、小结:1、知识要点:
2、思想方法:
五、作业:1、课本P80练习T1、2;
O
C
B
A
第2题
E
D
PAGE
2
