数学人教A版(2019)选择性必修第一册3.1.2 椭圆的简单几何性质(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.1.2 椭圆的简单几何性质(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 25.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-28 05:39:05 | ||
图片预览





文档简介
(共20张PPT)
3.1
椭圆
第三章
3.1.2 椭圆的简单几何性质
学习目标
1.掌握椭圆的范围、对称性、顶点、离心率等几何性质.
2.能利用椭圆的简单性质求标准方程.
3.能运用椭圆的简单几何性质分析和解决问题.
核心素养:数学抽象、逻辑推理、数学运算
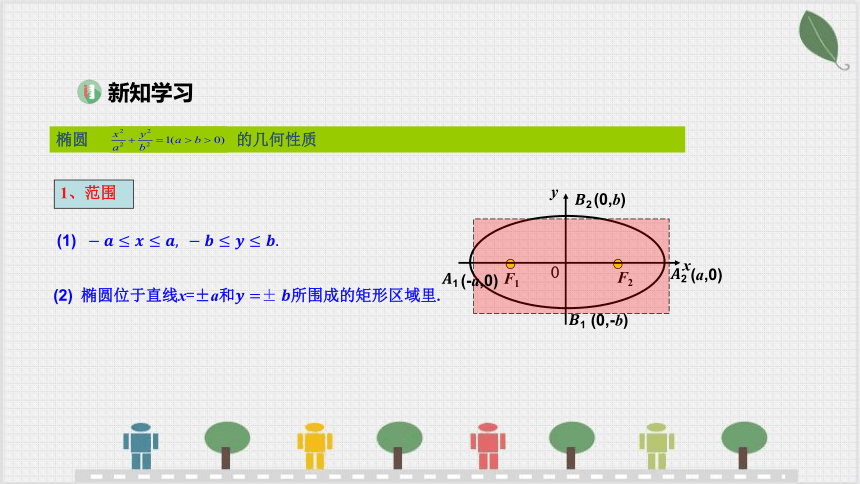
椭圆 的几何性质
(2) 椭圆位于直线x=±a和所围成的矩形区域里.
(1)
1、范围
x
F1
F2
O
y
1
2
1
2
(-a,0)
(0,-b)
(0,b)
(a,0)
新知学习
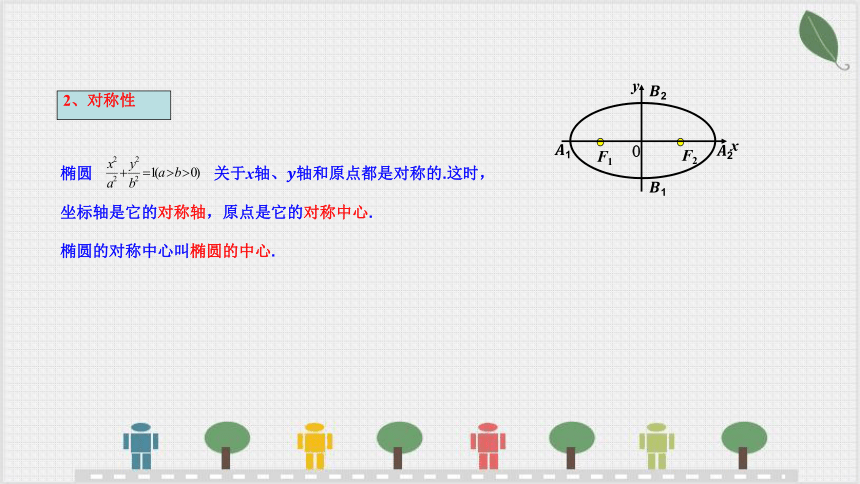
椭圆 关于x轴、轴和原点都是对称的.这时,
坐标轴是它的对称轴,原点是它的对称中心.
椭圆的对称中心叫椭圆的中心.
2、对称性
x
F1
F2
O
y
1
2
1
2
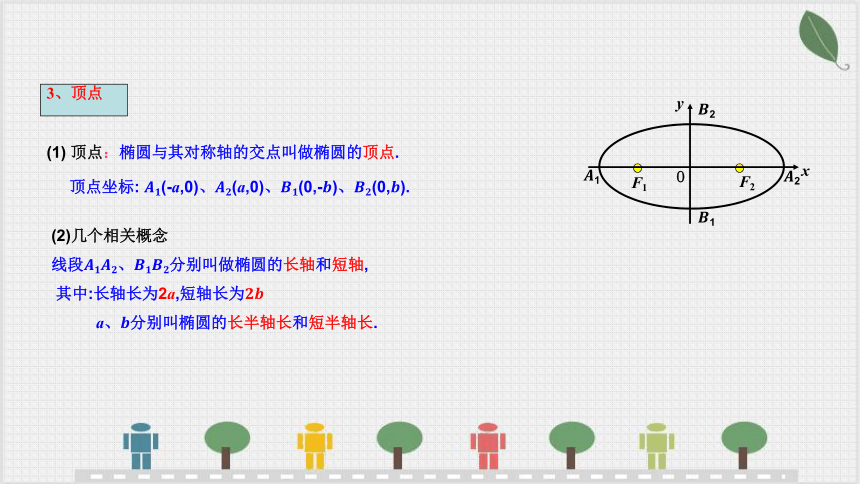
顶点坐标: (-a,0)、(a,0)、(0,-)、(0,).
(1) 顶点:椭圆与其对称轴的交点叫做椭圆的顶点.
(2)几个相关概念
线段、分别叫做椭圆的长轴和短轴,
其中:长轴长为2a,短轴长为
a、分别叫椭圆的长半轴长和短半轴长.
3、顶点
x
F1
F2
O
y
1
2
1
2
及时巩固 说出下列椭圆的顶点,焦点,焦距,长轴长,短轴长,长半轴长,短半轴长.
越大,椭圆越扁;越小,椭圆越圆.
(1)离心率的定义:
椭圆的焦距与长轴长的比 叫做椭圆的离心率.
(2)离心率的范围 :
(3)离心率对椭圆形状的影响:
4、离心率
变形公式:
如何刻画椭圆的圆扁程度?
及时巩固 求出下列椭圆的离心率.
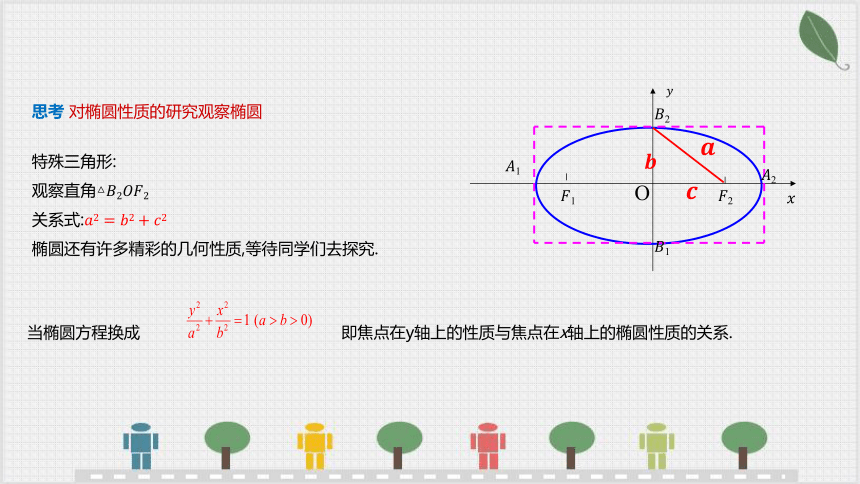
特殊三角形:
观察直角△
关系式:
椭圆还有许多精彩的几何性质,等待同学们去探究.
思考 对椭圆性质的研究观察椭圆
O
1
2
1
2
1
2
当椭圆方程换成 即焦点在y轴上的性质与焦点在x轴上的椭圆性质的关系.
方程
图形
范围
对称性
顶点
离心率
关于轴,轴,原点对称
关于轴,轴,原点对称
o
o
)
)
A1(0,-a)
例1 求椭圆的长轴和短轴的长、离心率、焦点和顶点的坐标.
解 把原方程化为标准方程,得
于是,a=5,=4,=
因此,椭圆的长轴长是_____,短轴的长是_____,
离心率___________,焦点坐标分别是_______________,
四个顶点坐标分别是______________________________.
2a=10
2b=8
F1(-3,0)和F2 (3,0)
A1(-5,0)、A2 (5,0)、B1(0,-4)和B2 (0,4)
一、已知椭圆的方程,探求其几何性质
(1)化标准,把椭圆方程化成标准形式;
(2)定位置,根据标准方程中对应分母的大小来确定焦点位置;
(3)求参数,写出的值,并求出c的值;
(4)写性质,按要求写出椭圆的简单几何性质.
反思感悟 确定椭圆几何性质的基本步骤
例2 求适合下列条件的椭圆的标准方程
(1)经过点;
(2)长轴是短轴的2倍,且过点(2,-6);
(3)长轴长为20, 离心率为0.6;
(4)在轴上的一个焦点与短轴的两个端点的连线相互垂直,且焦距为6
二、求椭圆的标准方程
答案
1.已知椭圆的几何性质,求其标准方程主要采用待定系数法,解题步骤为:
(1)确定焦点所在的位置,以确定椭圆标准方程的形式;
(2)确立关于的方程(组),求出参数;
(3)写出标准方程.
反思感悟 根据椭圆的性质求椭圆方程
2.在求椭圆方程时,要注意根据题目条件判断焦点所在的坐标轴,从而确定方程的形式,若不能确定焦点所在坐标轴,则应进行讨论.一般地,已知椭圆的焦点坐标时,可以确定焦点位置,而已知离心率、长轴长、短轴长、焦距时,则不能确定焦点位置.
跟踪训练 已知椭圆的长轴长是短轴长的2倍,且经过点,求椭圆的标准方程.
例3 设与定点的距离和它到直线 的距离的比是常数,求点的轨迹.
解 如图,设是点到直线的距离,
根据题意,动点的轨迹就是集合
∴
将上式两边平方,并化简,得
即
所以,点的轨迹是长轴、短轴长分别为10,6的椭圆.
二、求椭圆的标准方程
例4 如图,已知直线椭圆为何值时,直线椭圆: (1)有两个公共点?(2)有且只有一个公共点?(3)没有公共点?
解 由方程组
消去,得
①
方程①的根的判别式
三、 判断直线与椭圆的交点个数
由此时方程①有两个不相等的实数根,
直线l与椭圆有两个不同的公共点.
由此时方程①有两个相等的实数根,直线与椭圆有且只有公共点.
由此时方程①没有实数根,直线l与椭圆没有公共点.
①
例4 如图,已知直线椭圆为何值时,直线椭圆: (1)有两个公共点?(2)有且只有一个公共点?(3)没有公共点?
反思感悟 判断直线与椭圆个数的方法
这是求解直线与二次曲线有关问题的通法.
<0,
=0,
>0
(1)联立方程组
(2)消去一个未知数
(3)判断
方程
图形
范围
对称性
顶点
离心率
关于轴,轴,原点对称
关于轴,轴,原点对称
o
o
)
)
A1(0,-a)
课堂小结
3.1
椭圆
第三章
3.1.2 椭圆的简单几何性质
学习目标
1.掌握椭圆的范围、对称性、顶点、离心率等几何性质.
2.能利用椭圆的简单性质求标准方程.
3.能运用椭圆的简单几何性质分析和解决问题.
核心素养:数学抽象、逻辑推理、数学运算
椭圆 的几何性质
(2) 椭圆位于直线x=±a和所围成的矩形区域里.
(1)
1、范围
x
F1
F2
O
y
1
2
1
2
(-a,0)
(0,-b)
(0,b)
(a,0)
新知学习
椭圆 关于x轴、轴和原点都是对称的.这时,
坐标轴是它的对称轴,原点是它的对称中心.
椭圆的对称中心叫椭圆的中心.
2、对称性
x
F1
F2
O
y
1
2
1
2
顶点坐标: (-a,0)、(a,0)、(0,-)、(0,).
(1) 顶点:椭圆与其对称轴的交点叫做椭圆的顶点.
(2)几个相关概念
线段、分别叫做椭圆的长轴和短轴,
其中:长轴长为2a,短轴长为
a、分别叫椭圆的长半轴长和短半轴长.
3、顶点
x
F1
F2
O
y
1
2
1
2
及时巩固 说出下列椭圆的顶点,焦点,焦距,长轴长,短轴长,长半轴长,短半轴长.
越大,椭圆越扁;越小,椭圆越圆.
(1)离心率的定义:
椭圆的焦距与长轴长的比 叫做椭圆的离心率.
(2)离心率的范围 :
(3)离心率对椭圆形状的影响:
4、离心率
变形公式:
如何刻画椭圆的圆扁程度?
及时巩固 求出下列椭圆的离心率.
特殊三角形:
观察直角△
关系式:
椭圆还有许多精彩的几何性质,等待同学们去探究.
思考 对椭圆性质的研究观察椭圆
O
1
2
1
2
1
2
当椭圆方程换成 即焦点在y轴上的性质与焦点在x轴上的椭圆性质的关系.
方程
图形
范围
对称性
顶点
离心率
关于轴,轴,原点对称
关于轴,轴,原点对称
o
o
)
)
A1(0,-a)
例1 求椭圆的长轴和短轴的长、离心率、焦点和顶点的坐标.
解 把原方程化为标准方程,得
于是,a=5,=4,=
因此,椭圆的长轴长是_____,短轴的长是_____,
离心率___________,焦点坐标分别是_______________,
四个顶点坐标分别是______________________________.
2a=10
2b=8
F1(-3,0)和F2 (3,0)
A1(-5,0)、A2 (5,0)、B1(0,-4)和B2 (0,4)
一、已知椭圆的方程,探求其几何性质
(1)化标准,把椭圆方程化成标准形式;
(2)定位置,根据标准方程中对应分母的大小来确定焦点位置;
(3)求参数,写出的值,并求出c的值;
(4)写性质,按要求写出椭圆的简单几何性质.
反思感悟 确定椭圆几何性质的基本步骤
例2 求适合下列条件的椭圆的标准方程
(1)经过点;
(2)长轴是短轴的2倍,且过点(2,-6);
(3)长轴长为20, 离心率为0.6;
(4)在轴上的一个焦点与短轴的两个端点的连线相互垂直,且焦距为6
二、求椭圆的标准方程
答案
1.已知椭圆的几何性质,求其标准方程主要采用待定系数法,解题步骤为:
(1)确定焦点所在的位置,以确定椭圆标准方程的形式;
(2)确立关于的方程(组),求出参数;
(3)写出标准方程.
反思感悟 根据椭圆的性质求椭圆方程
2.在求椭圆方程时,要注意根据题目条件判断焦点所在的坐标轴,从而确定方程的形式,若不能确定焦点所在坐标轴,则应进行讨论.一般地,已知椭圆的焦点坐标时,可以确定焦点位置,而已知离心率、长轴长、短轴长、焦距时,则不能确定焦点位置.
跟踪训练 已知椭圆的长轴长是短轴长的2倍,且经过点,求椭圆的标准方程.
例3 设与定点的距离和它到直线 的距离的比是常数,求点的轨迹.
解 如图,设是点到直线的距离,
根据题意,动点的轨迹就是集合
∴
将上式两边平方,并化简,得
即
所以,点的轨迹是长轴、短轴长分别为10,6的椭圆.
二、求椭圆的标准方程
例4 如图,已知直线椭圆为何值时,直线椭圆: (1)有两个公共点?(2)有且只有一个公共点?(3)没有公共点?
解 由方程组
消去,得
①
方程①的根的判别式
三、 判断直线与椭圆的交点个数
由此时方程①有两个不相等的实数根,
直线l与椭圆有两个不同的公共点.
由此时方程①有两个相等的实数根,直线与椭圆有且只有公共点.
由此时方程①没有实数根,直线l与椭圆没有公共点.
①
例4 如图,已知直线椭圆为何值时,直线椭圆: (1)有两个公共点?(2)有且只有一个公共点?(3)没有公共点?
反思感悟 判断直线与椭圆个数的方法
这是求解直线与二次曲线有关问题的通法.
<0,
=0,
>0
(1)联立方程组
(2)消去一个未知数
(3)判断
方程
图形
范围
对称性
顶点
离心率
关于轴,轴,原点对称
关于轴,轴,原点对称
o
o
)
)
A1(0,-a)
课堂小结
