北京市昌平区2022- 2023学年初三年级双城融合第一学期期中质量监控数学试卷(word,无答案)
文档属性
| 名称 | 北京市昌平区2022- 2023学年初三年级双城融合第一学期期中质量监控数学试卷(word,无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 353.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-27 00:00:00 | ||
图片预览

文档简介
2022 - 2023学年第一学期昌平区双城融合学区
初三年级数学学科期中质量抽测
数学试卷
2022.10
本试卷共7页,共100分。考试时长120分钟。考生务必将答案填涂或书写在答题卡上,在试卷上作答无效。考试结束后,将答题卡交回。
一、选择题(本题共16分,每小题2分)第1 - 8题均有四个选项,符合题意的选项只有一个.
1. 下列各组线段(单位:cm)中,是成比例线段的是( ).
A. 1,2,3,4 B. 1,2,2,4 C. 3,5,9,13 D. 1,2,2,3
2.抛物线的顶点坐标是( ).
A.(-2,0) B. (2,0) C. (0,2) D. (0,-2)
3. 如果一个矩形的宽与长的比等于黄金数(约为0.618),就称这个矩形为黄金矩形.若矩形ABCD为黄金矩形,宽AD=,则长AB为( ).
A.1 B.-1 C.2 D.-2
4.若将抛物线先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线的表达式是( ).
A. B. C. D.
5.如图,在□ABCD中,E是AB的中点,EC交BD于点F,
那么EF与CF的比是( ).
A.2∶1 B.1∶3
C. 1∶2 D. 3∶1
6. 如图,△ABC∽△A’B’C’,AD和A’D’分别是△ABC和△A’B’C’的高,
若AD=2,A’D’=3,则△ABC与△A’B’C’的面积的比为( ).
4:9 B. 9:4 C. 2:3 D. 3:2
7.已知二次函数的部分图象如图所示,则使得函数值y大于2的自变量x的取值可以是( ).
A.-4 B.-2 C.0 D.2
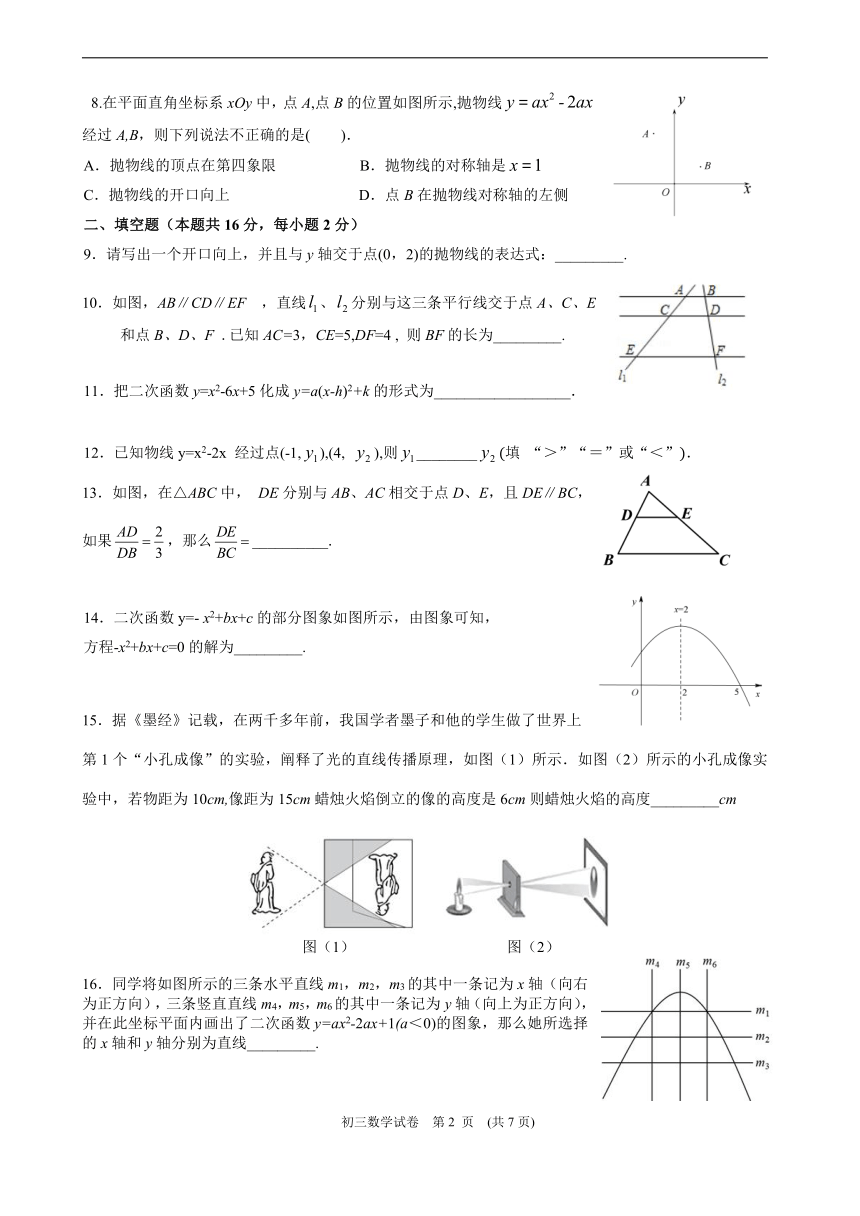
8.在平面直角坐标系xOy中,点A,点B的位置如图所示,抛物线经过A,B,则下列说法不正确的是( ).
A.抛物线的顶点在第四象限 B.抛物线的对称轴是
C.抛物线的开口向上 D.点B在抛物线对称轴的左侧
二、填空题(本题共16分,每小题2分)
9.请写出一个开口向上,并且与y轴交于点(0,2)的抛物线的表达式:_________.
10.如图,AB∥CD∥EF ,直线、分别与这三条平行线交于点A、C、E 和点B、D、F .已知AC=3,CE=5,DF=4 , 则BF的长为_________.
11.把二次函数y=x2-6x+5化成y=a(x-h)2+k的形式为__________________.
12.已知物线y=x2-2x 经过点(-1,),(4, ),则________填 “>”“=”或“<”.
13.如图,在△ABC中, DE分别与AB、AC相交于点D、E,且DE∥BC,如果,那么__________.
14.二次函数y=- x2+bx+c的部分图象如图所示,由图象可知,
方程-x2+bx+c=0的解为_________.
15.据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验,阐释了光的直线传播原理,如图(1)所示.如图(2)所示的小孔成像实验中,若物距为10cm,像距为15cm蜡烛火焰倒立的像的高度是6cm则蜡烛火焰的高度_________cm
图(1) 图(2)
16.同学将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了二次函数y=ax2-2ax+1(a<0)的图象,那么她所选择的x轴和y轴分别为直线_________.
三、解答题(本题共12小题,第17 - 22题,每小题5分,第23 - 26题,每小题6分,第27、28题,每小题7分,共68分)
17.已知二次函数 y = x2+2x-3.
(1)求该二次函数的图象的对称轴和顶点坐标;
(2)求该二次函数的图象与x轴交点.
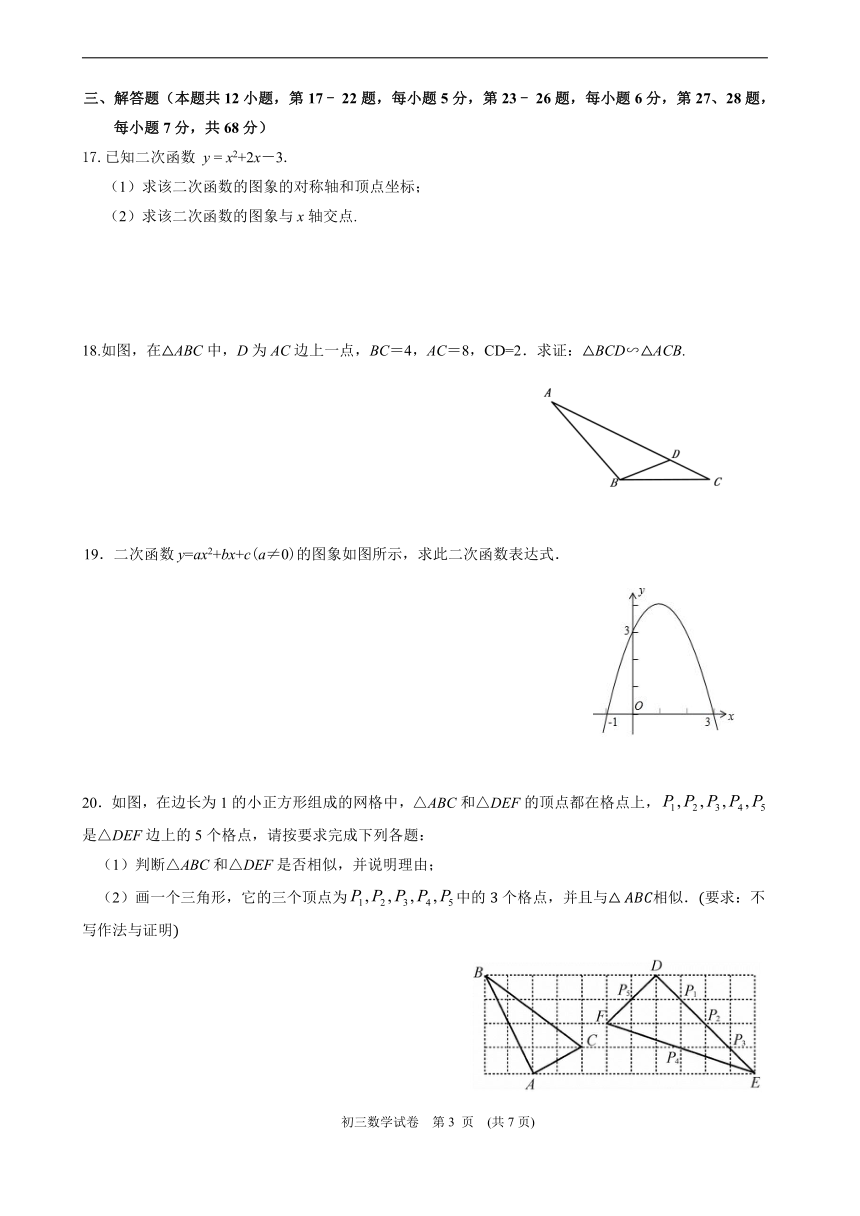
18.如图,在△ABC中,D为AC边上一点,BC=4,AC=8,CD=2.求证:△BCD∽△ACB.
19.二次函数y=ax2+bx+c(a≠0)的图象如图所示,求此二次函数表达式.
20.如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,是△DEF边上的5个格点,请按要求完成下列各题:
(1)判断△ABC和△DEF是否相似,并说明理由;
(2)画一个三角形,它的三个顶点为中的个格点,并且与相似.要求:不写作法与证明
21.在平面直角坐标系xOy中,二次函数图象上部分点的横坐标x,纵坐标y的对应值
如下表:
x … -1 0 1 2 …
y … -3 0 1 0 …
(1)求这个二次函数的表达式;
(2)画出这个二次函数的图象;
(3)若,结合函数图象,直接写出x的取值范围.
22.如图,将一个Rt△BPE与正方形ABCD 叠放在一起,并使其直角顶点P落在线段CD上(不与C,D两点重合),斜边的一部分与线段AB重合.
(1)图中与Rt△BCP相似的三角形共有________个,分别是
__________________________________________;
(2)请选择第(1)问答案中的任意一个三角形,完成该三角形与△BCP相似的证明.
23.如图,在矩形ABCD中,E为BC的中点,DF⊥AE ,垂足为F,AB=6,BC=4,
求AE,DF的长.
24.掷实心球是高中阶段学校招生体育考试的选考项目.如图1是一名女生投实心球,实心球行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图2所示,掷出时起点处高度为,当水平距离为3m时,实心球行进至最高点3m处.
(1)求y关于x的函数表达式;
(2)根据高中阶段学校招生体育考试评分标准女生,投掷过程中,实心球从起点到落地点的水平距离大于等于6.70m,此项考试得分为满分10分.该女生在此项考试中是否得满分,请说明理由.
图1 图2
25.跳台滑雪是冬季奥运会比赛项目之一 .记运动员在该项目的运动过程中的某个位置与起跳点的水平距离为x(单位:m),竖直高度为y(单位:m),下面记录了甲运动员起跳后的运动过程中的七组数据
x/m 0 10 20 30 40 50 60
y/m 54.0 57.8 57.6 53.4 45.2 33.0 16.8
下面是小明的探究过程,请补充完整:
(1)为观察y与x之间的关系,建立坐标系,以x为横坐标,y为纵坐标,描出表中数据对应的7个点,并用平滑的曲线连接它们;
(2) 观察发现,(1)中的曲线可以看作是 的一部分(填“抛物线”或“双曲线”),结合图象,可推断出水平距离约为 m(结果保留小数点后一位)时,甲运动员起跳后达到最高点;
(3) 乙运动员在此跳台进行训练,若乙运动员在运动过程中的最高点的竖直高度达到61 m,则乙运动员运动中的最高点比甲运动员运动中的最高点 (填写“高”或“低”)约 m (结果保留小数点后一位).
26.在平面直角坐标系xOy中,抛物线(a≠0)与y轴交于点A.
(1)直接写出点A的坐标;
(2)点A、B关于对称轴对称,求点B的坐标;
(3)已知点,.若抛物线与线段PQ恰有两个公共点,结合函数图象,求a的取值范围.
27.感知:数学课上,老师给出了一个模型:如图1,点A在直线DE上,且∠BDA=∠BAC=∠AEC=90o,像这种一条直线上的三个顶点含有三个相等的角的模型我们把它称为“一线三等角“模型.
应用:(1)如图2,Rt ABC中,∠ACB=90o,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.求证:△BEC≌△CDA.
(2)如图3,在 ABCD中,E为边BC上的一点,F为边AB上的一点.若∠DEF=∠B,AB=10,BE=6,求的值.
28.对某一个函数给出如下定义:如果存在实数M, 对于任意的函数值y,都满足y ≤ M,那么称这个函数是有上界函数. 在所有满足条件的M中,其最小值称为这个函数的上确界. 例如,图中的函数是有上界函数,其上确界是2.
(1)函数①和②(x ≤ 2)中是有上界函数的为 (只填序号即可),其上确界为 ;
(2)如果函数(a ≤x≤ b,b > a)的上确界是b,且这个函数的最小值不超过,求a的取值范围;
(3)如果函数(1≤x≤5)是以3为上确界的有上界函数,求实数a的值.
初三数学试卷 第1
初三年级数学学科期中质量抽测
数学试卷
2022.10
本试卷共7页,共100分。考试时长120分钟。考生务必将答案填涂或书写在答题卡上,在试卷上作答无效。考试结束后,将答题卡交回。
一、选择题(本题共16分,每小题2分)第1 - 8题均有四个选项,符合题意的选项只有一个.
1. 下列各组线段(单位:cm)中,是成比例线段的是( ).
A. 1,2,3,4 B. 1,2,2,4 C. 3,5,9,13 D. 1,2,2,3
2.抛物线的顶点坐标是( ).
A.(-2,0) B. (2,0) C. (0,2) D. (0,-2)
3. 如果一个矩形的宽与长的比等于黄金数(约为0.618),就称这个矩形为黄金矩形.若矩形ABCD为黄金矩形,宽AD=,则长AB为( ).
A.1 B.-1 C.2 D.-2
4.若将抛物线先向左平移3个单位,再向下平移2个单位,得到新的抛物线,则新抛物线的表达式是( ).
A. B. C. D.
5.如图,在□ABCD中,E是AB的中点,EC交BD于点F,
那么EF与CF的比是( ).
A.2∶1 B.1∶3
C. 1∶2 D. 3∶1
6. 如图,△ABC∽△A’B’C’,AD和A’D’分别是△ABC和△A’B’C’的高,
若AD=2,A’D’=3,则△ABC与△A’B’C’的面积的比为( ).
4:9 B. 9:4 C. 2:3 D. 3:2
7.已知二次函数的部分图象如图所示,则使得函数值y大于2的自变量x的取值可以是( ).
A.-4 B.-2 C.0 D.2
8.在平面直角坐标系xOy中,点A,点B的位置如图所示,抛物线经过A,B,则下列说法不正确的是( ).
A.抛物线的顶点在第四象限 B.抛物线的对称轴是
C.抛物线的开口向上 D.点B在抛物线对称轴的左侧
二、填空题(本题共16分,每小题2分)
9.请写出一个开口向上,并且与y轴交于点(0,2)的抛物线的表达式:_________.
10.如图,AB∥CD∥EF ,直线、分别与这三条平行线交于点A、C、E 和点B、D、F .已知AC=3,CE=5,DF=4 , 则BF的长为_________.
11.把二次函数y=x2-6x+5化成y=a(x-h)2+k的形式为__________________.
12.已知物线y=x2-2x 经过点(-1,),(4, ),则________填 “>”“=”或“<”.
13.如图,在△ABC中, DE分别与AB、AC相交于点D、E,且DE∥BC,如果,那么__________.
14.二次函数y=- x2+bx+c的部分图象如图所示,由图象可知,
方程-x2+bx+c=0的解为_________.
15.据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验,阐释了光的直线传播原理,如图(1)所示.如图(2)所示的小孔成像实验中,若物距为10cm,像距为15cm蜡烛火焰倒立的像的高度是6cm则蜡烛火焰的高度_________cm
图(1) 图(2)
16.同学将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了二次函数y=ax2-2ax+1(a<0)的图象,那么她所选择的x轴和y轴分别为直线_________.
三、解答题(本题共12小题,第17 - 22题,每小题5分,第23 - 26题,每小题6分,第27、28题,每小题7分,共68分)
17.已知二次函数 y = x2+2x-3.
(1)求该二次函数的图象的对称轴和顶点坐标;
(2)求该二次函数的图象与x轴交点.
18.如图,在△ABC中,D为AC边上一点,BC=4,AC=8,CD=2.求证:△BCD∽△ACB.
19.二次函数y=ax2+bx+c(a≠0)的图象如图所示,求此二次函数表达式.
20.如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,是△DEF边上的5个格点,请按要求完成下列各题:
(1)判断△ABC和△DEF是否相似,并说明理由;
(2)画一个三角形,它的三个顶点为中的个格点,并且与相似.要求:不写作法与证明
21.在平面直角坐标系xOy中,二次函数图象上部分点的横坐标x,纵坐标y的对应值
如下表:
x … -1 0 1 2 …
y … -3 0 1 0 …
(1)求这个二次函数的表达式;
(2)画出这个二次函数的图象;
(3)若,结合函数图象,直接写出x的取值范围.
22.如图,将一个Rt△BPE与正方形ABCD 叠放在一起,并使其直角顶点P落在线段CD上(不与C,D两点重合),斜边的一部分与线段AB重合.
(1)图中与Rt△BCP相似的三角形共有________个,分别是
__________________________________________;
(2)请选择第(1)问答案中的任意一个三角形,完成该三角形与△BCP相似的证明.
23.如图,在矩形ABCD中,E为BC的中点,DF⊥AE ,垂足为F,AB=6,BC=4,
求AE,DF的长.
24.掷实心球是高中阶段学校招生体育考试的选考项目.如图1是一名女生投实心球,实心球行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图2所示,掷出时起点处高度为,当水平距离为3m时,实心球行进至最高点3m处.
(1)求y关于x的函数表达式;
(2)根据高中阶段学校招生体育考试评分标准女生,投掷过程中,实心球从起点到落地点的水平距离大于等于6.70m,此项考试得分为满分10分.该女生在此项考试中是否得满分,请说明理由.
图1 图2
25.跳台滑雪是冬季奥运会比赛项目之一 .记运动员在该项目的运动过程中的某个位置与起跳点的水平距离为x(单位:m),竖直高度为y(单位:m),下面记录了甲运动员起跳后的运动过程中的七组数据
x/m 0 10 20 30 40 50 60
y/m 54.0 57.8 57.6 53.4 45.2 33.0 16.8
下面是小明的探究过程,请补充完整:
(1)为观察y与x之间的关系,建立坐标系,以x为横坐标,y为纵坐标,描出表中数据对应的7个点,并用平滑的曲线连接它们;
(2) 观察发现,(1)中的曲线可以看作是 的一部分(填“抛物线”或“双曲线”),结合图象,可推断出水平距离约为 m(结果保留小数点后一位)时,甲运动员起跳后达到最高点;
(3) 乙运动员在此跳台进行训练,若乙运动员在运动过程中的最高点的竖直高度达到61 m,则乙运动员运动中的最高点比甲运动员运动中的最高点 (填写“高”或“低”)约 m (结果保留小数点后一位).
26.在平面直角坐标系xOy中,抛物线(a≠0)与y轴交于点A.
(1)直接写出点A的坐标;
(2)点A、B关于对称轴对称,求点B的坐标;
(3)已知点,.若抛物线与线段PQ恰有两个公共点,结合函数图象,求a的取值范围.
27.感知:数学课上,老师给出了一个模型:如图1,点A在直线DE上,且∠BDA=∠BAC=∠AEC=90o,像这种一条直线上的三个顶点含有三个相等的角的模型我们把它称为“一线三等角“模型.
应用:(1)如图2,Rt ABC中,∠ACB=90o,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.求证:△BEC≌△CDA.
(2)如图3,在 ABCD中,E为边BC上的一点,F为边AB上的一点.若∠DEF=∠B,AB=10,BE=6,求的值.
28.对某一个函数给出如下定义:如果存在实数M, 对于任意的函数值y,都满足y ≤ M,那么称这个函数是有上界函数. 在所有满足条件的M中,其最小值称为这个函数的上确界. 例如,图中的函数是有上界函数,其上确界是2.
(1)函数①和②(x ≤ 2)中是有上界函数的为 (只填序号即可),其上确界为 ;
(2)如果函数(a ≤x≤ b,b > a)的上确界是b,且这个函数的最小值不超过,求a的取值范围;
(3)如果函数(1≤x≤5)是以3为上确界的有上界函数,求实数a的值.
初三数学试卷 第1
同课章节目录
