总复习(课件)人教版五年级下册数学(共25张PPT)
文档属性
| 名称 | 总复习(课件)人教版五年级下册数学(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 431.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-27 21:54:04 | ||
图片预览








文档简介
(共25张PPT)
总 复 习
观察物体(三)
因数和倍数
长方体和正方体
分数的意义和性质
找次品
折线统计图
分数的加法和减法
图形的运动(三)
观察物体(三)
先数看到几个面,再看它的排列法
从前面看
从左面看
从上面看
站在任意一个位置,最多能看到物体的几个面?
因数和倍数
1.因数和倍数
2.2、5、3的倍数的特征
3.质数和合数
1.因数和倍数
在整数除法中,如果商是整数而没有余数,我们就说被除数是除数的倍数,除数是被除数的因数。
因数与倍数是相互依存的。
一个数的最小因数是1,最大因数是它本身,一个数的因数的个数是有限的;
一个数的最小倍数是它本身,没有最大倍数一个数的倍数的个数是无限的。
14的因数有( )
1,2,7,14
2.2、5、3的倍数的特征
个位上是0、2、4、6、8的数都是2的倍数。
在自然数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
个位上是0或5的数,是5的倍数。
如果一个数同时是2和5的倍数,那它的个位上的数字一定是0.
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
一个六位数20□15□是2、3和5的倍数,这个数可能是( )、
( )和( )
201150
204150
207150
三个连续奇数的和是150,这三个数中最小数是多少?其中最大的数是多少?
2.2、5、3的倍数的特征
150÷3=50 50-2=48 50+2=52
答:这三个数中的最小数是48,最大数是52。
3.质数和合数
一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数);
一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。
1既不是质数也不是合数。
把30分解质因数应该写成( )
A、30=1×2×3×5 B、30=6×5 C、30=2×3×5
C
长方体和正方体
1.长方体和正方体的认识
2.长方体和正方体的表面积
3.长方体和正方体的体积
4.容积和单位换算
1.长方体和正方体的认识
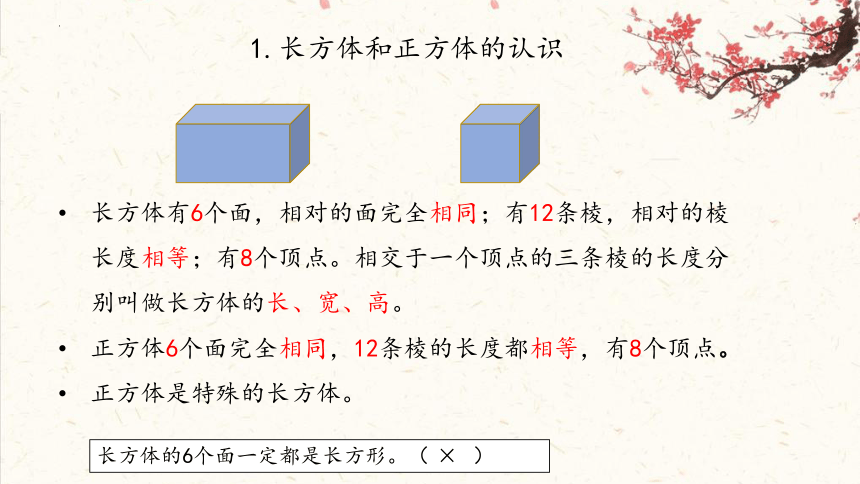
长方体有6个面,相对的面完全相同;有12条棱,相对的棱长度相等;有8个顶点。相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
正方体6个面完全相同,12条棱的长度都相等,有8个顶点。
正方体是特殊的长方体。
长方体的6个面一定都是长方形。( )
×
1.长方体和正方体的认识
长方体的棱长总和=(长+宽+高)×4
正方体的棱长总和=棱长×12
用一根铁丝可以做成一个长11cm、宽7cm、高3cm的长方体框架,如果把它改做成一个正方体框架,这个正方体框架的棱长是多少
(11+7+3)×4÷12
=21×4÷12
=84÷12
=7(cm) 答:这个正方体框架的棱长是7cm。
2.长方体和正方体的表面积
长方体或正方体6个面的总面积,叫做它的表面积。
长方体的表面积=(长×宽+长×高+宽×高)×2
正方体的表面积=棱长×棱长×6
无盖或无底长方体的表面积=(长×高+宽×高)×2+长×宽
把两个棱长是4厘米的正方体粘合成一个长方体,这个长方体的表面积是( )。
80平方厘米
3.长方体和正方体的体积
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
一个长方体的体积是120立方分米,高是6分米,宽是2分米,长是( )分米。
10
4.容积和单位换算
容器所能容纳物体的体积,叫做它们的容积。
容积的计算方法与体积的计算方法相同。
1=1000, 1000=1
1L=1000mL 1000mL=1L
1L=1 1mL=1
1、物体的体积等于它的容积。( )
2、2.85立方米=( )立方分米 3升20毫升=( )升
×
2850
3.02
分数的意义和性质
1.分数的意义
2.真分数和假分数
3.分数的基本性质
4.约分
5.通分
6.分数和小数的互化
1.分数的意义
一个物体、一个计量单位或一些物体都可以看作一个整体,把这个整体平均分成若干份,这样的一份或几份可以用分数来表示。
把单位“1”平均分成若干份,表示其中一份的数叫做分数单位。
把5米长的绳子平均分成8段,每段是全长的( )
2.真分数、假分数和带分数
分子比分母小的分数叫做真分数。真分数<1。
分子比分母大或分子和分母相等的分数叫做假分数。假分数≥1。
由整数(不包括0)和真分数合成的数叫做带分数。带分数>1。
假分数可以化成整数或带分数。
在里,当a是( )时,这个分数是7,当a是( )时,这个分数时1.
1
7
3.分数的基本性质
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变,这就是分数的基本性质。
的分子加上5,如果要使这个分数的大小不变,分母应该( )。
A、加上5 B、加上14 C、加上7
C
=
20
4
4.约分
几个数公有的因数,叫做它们的公因数;其中最大的叫做它们的最大公因数。
把一个分数化成和它相等,但分子和分母都比较小的分数,叫做约分。
约分时分子和分母要同时除以他们的公因数。
计算结果一定要约分化成最简分数。
两个数为互质数,它们的最大公因数为1.
两个数为倍数关系,它们的最大公因数是较小数。
5.通分
几个数公有的倍数,叫做它们的公倍数;其中最小的叫做它们的最小公倍数。
把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
通分选取分母的最小公倍数作为公分母进行通分。
两个数为互质数,它们的最小公倍数是两个数的乘积。
两个数为倍数关系,它们的最小公倍数是较大数。
五年级同学们排队,10人一行和12人一行都正好排好,这个班至少有多少人?
2 10 12
5 6
最小公倍数:2×5×6=60
答:这个班至少有60人。
6.分数和小数的互化
分母是10,100,1000,……的分数可以直接化成小数。
分母不是10,100,1000,……的分数化成小数,用分子除以分母,除不尽时,要根据需要按“四舍五入”法保留小数位数。
图形的运动(三)
物体绕某一点向某一方向转动一定的角度,这种现象叫做旋转。如风车的运动。
旋转的三要素是旋转中心、旋转方向和旋转角度。
图形旋转的特征:图形旋转后,形状、大小都没有变化,只是位置发生了变化。
分数的加法和减法
同分母分数相加、减,分母不变,只把分子相加、减。
异分母分数相加、减,先通分,然后按照同分母分数加、减法进行计算。
计算的结果能约分的要约成最简分数。
分数加减法与整数加减法的混合运算顺序和运算定律一样。
+ -
70-3 - 4
=70-(3 + 4)
=70-8
=62
= - +
= + =
折线统计图
单式折线统计图只能看出一组数据变化的整体趋势。
复式折线统计图可以比较方便地比较两组数据的变化趋势。
画复式折线统计图时,要先确定图例,按照图例画。
找次品
找次品的最佳方法:分成3份,尽量平均分,称的次数最少。
总 复 习
观察物体(三)
因数和倍数
长方体和正方体
分数的意义和性质
找次品
折线统计图
分数的加法和减法
图形的运动(三)
观察物体(三)
先数看到几个面,再看它的排列法
从前面看
从左面看
从上面看
站在任意一个位置,最多能看到物体的几个面?
因数和倍数
1.因数和倍数
2.2、5、3的倍数的特征
3.质数和合数
1.因数和倍数
在整数除法中,如果商是整数而没有余数,我们就说被除数是除数的倍数,除数是被除数的因数。
因数与倍数是相互依存的。
一个数的最小因数是1,最大因数是它本身,一个数的因数的个数是有限的;
一个数的最小倍数是它本身,没有最大倍数一个数的倍数的个数是无限的。
14的因数有( )
1,2,7,14
2.2、5、3的倍数的特征
个位上是0、2、4、6、8的数都是2的倍数。
在自然数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
个位上是0或5的数,是5的倍数。
如果一个数同时是2和5的倍数,那它的个位上的数字一定是0.
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
一个六位数20□15□是2、3和5的倍数,这个数可能是( )、
( )和( )
201150
204150
207150
三个连续奇数的和是150,这三个数中最小数是多少?其中最大的数是多少?
2.2、5、3的倍数的特征
150÷3=50 50-2=48 50+2=52
答:这三个数中的最小数是48,最大数是52。
3.质数和合数
一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数);
一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。
1既不是质数也不是合数。
把30分解质因数应该写成( )
A、30=1×2×3×5 B、30=6×5 C、30=2×3×5
C
长方体和正方体
1.长方体和正方体的认识
2.长方体和正方体的表面积
3.长方体和正方体的体积
4.容积和单位换算
1.长方体和正方体的认识
长方体有6个面,相对的面完全相同;有12条棱,相对的棱长度相等;有8个顶点。相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
正方体6个面完全相同,12条棱的长度都相等,有8个顶点。
正方体是特殊的长方体。
长方体的6个面一定都是长方形。( )
×
1.长方体和正方体的认识
长方体的棱长总和=(长+宽+高)×4
正方体的棱长总和=棱长×12
用一根铁丝可以做成一个长11cm、宽7cm、高3cm的长方体框架,如果把它改做成一个正方体框架,这个正方体框架的棱长是多少
(11+7+3)×4÷12
=21×4÷12
=84÷12
=7(cm) 答:这个正方体框架的棱长是7cm。
2.长方体和正方体的表面积
长方体或正方体6个面的总面积,叫做它的表面积。
长方体的表面积=(长×宽+长×高+宽×高)×2
正方体的表面积=棱长×棱长×6
无盖或无底长方体的表面积=(长×高+宽×高)×2+长×宽
把两个棱长是4厘米的正方体粘合成一个长方体,这个长方体的表面积是( )。
80平方厘米
3.长方体和正方体的体积
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
一个长方体的体积是120立方分米,高是6分米,宽是2分米,长是( )分米。
10
4.容积和单位换算
容器所能容纳物体的体积,叫做它们的容积。
容积的计算方法与体积的计算方法相同。
1=1000, 1000=1
1L=1000mL 1000mL=1L
1L=1 1mL=1
1、物体的体积等于它的容积。( )
2、2.85立方米=( )立方分米 3升20毫升=( )升
×
2850
3.02
分数的意义和性质
1.分数的意义
2.真分数和假分数
3.分数的基本性质
4.约分
5.通分
6.分数和小数的互化
1.分数的意义
一个物体、一个计量单位或一些物体都可以看作一个整体,把这个整体平均分成若干份,这样的一份或几份可以用分数来表示。
把单位“1”平均分成若干份,表示其中一份的数叫做分数单位。
把5米长的绳子平均分成8段,每段是全长的( )
2.真分数、假分数和带分数
分子比分母小的分数叫做真分数。真分数<1。
分子比分母大或分子和分母相等的分数叫做假分数。假分数≥1。
由整数(不包括0)和真分数合成的数叫做带分数。带分数>1。
假分数可以化成整数或带分数。
在里,当a是( )时,这个分数是7,当a是( )时,这个分数时1.
1
7
3.分数的基本性质
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变,这就是分数的基本性质。
的分子加上5,如果要使这个分数的大小不变,分母应该( )。
A、加上5 B、加上14 C、加上7
C
=
20
4
4.约分
几个数公有的因数,叫做它们的公因数;其中最大的叫做它们的最大公因数。
把一个分数化成和它相等,但分子和分母都比较小的分数,叫做约分。
约分时分子和分母要同时除以他们的公因数。
计算结果一定要约分化成最简分数。
两个数为互质数,它们的最大公因数为1.
两个数为倍数关系,它们的最大公因数是较小数。
5.通分
几个数公有的倍数,叫做它们的公倍数;其中最小的叫做它们的最小公倍数。
把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
通分选取分母的最小公倍数作为公分母进行通分。
两个数为互质数,它们的最小公倍数是两个数的乘积。
两个数为倍数关系,它们的最小公倍数是较大数。
五年级同学们排队,10人一行和12人一行都正好排好,这个班至少有多少人?
2 10 12
5 6
最小公倍数:2×5×6=60
答:这个班至少有60人。
6.分数和小数的互化
分母是10,100,1000,……的分数可以直接化成小数。
分母不是10,100,1000,……的分数化成小数,用分子除以分母,除不尽时,要根据需要按“四舍五入”法保留小数位数。
图形的运动(三)
物体绕某一点向某一方向转动一定的角度,这种现象叫做旋转。如风车的运动。
旋转的三要素是旋转中心、旋转方向和旋转角度。
图形旋转的特征:图形旋转后,形状、大小都没有变化,只是位置发生了变化。
分数的加法和减法
同分母分数相加、减,分母不变,只把分子相加、减。
异分母分数相加、减,先通分,然后按照同分母分数加、减法进行计算。
计算的结果能约分的要约成最简分数。
分数加减法与整数加减法的混合运算顺序和运算定律一样。
+ -
70-3 - 4
=70-(3 + 4)
=70-8
=62
= - +
= + =
折线统计图
单式折线统计图只能看出一组数据变化的整体趋势。
复式折线统计图可以比较方便地比较两组数据的变化趋势。
画复式折线统计图时,要先确定图例,按照图例画。
找次品
找次品的最佳方法:分成3份,尽量平均分,称的次数最少。
