湘教版数学八年级上册 第3章小结与复习课件(共30张PPT)
文档属性
| 名称 | 湘教版数学八年级上册 第3章小结与复习课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 48.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-28 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
第3章 实 数
小结与复习
1. 平方根的概念及性质
2. 算术平方根的概念及性质
(2)性质:正数a有两个平方根,它们互为相反数;
0的平方根是0,负数没有平方根.
(2)性质:0的算术平方根是0,只有非负数才有算术平方根,而且
算术平方根也是非负数.
一、平方根
(1)定义:若r2=a,则r叫作a的一个平方根.
(1)定义:a的正平方根叫作a的算术平方根.
要点梳理
3. 无理数
常见类型: 带根号且开不尽方的数;
含π的一些数;
无限不循环小数.
二、立方根
1. 立方根的概念及性质
(1)定义:如果b3=a,那么b叫作a的立方根.
(2)性质:每一个实数都有一个与它本身符号相同的立方根.
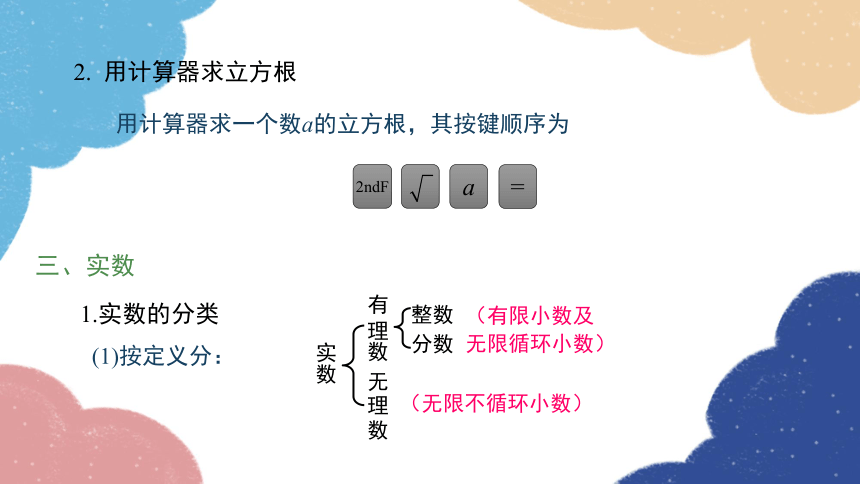
2. 用计算器求立方根
用计算器求一个数a的立方根,其按键顺序为
2ndF
a
=
三、实数
1.实数的分类
(1)按定义分:
实数
有
理
数
分数
整数
无
理
数
(有限小数及
无限循环小数)
(无限不循环小数)
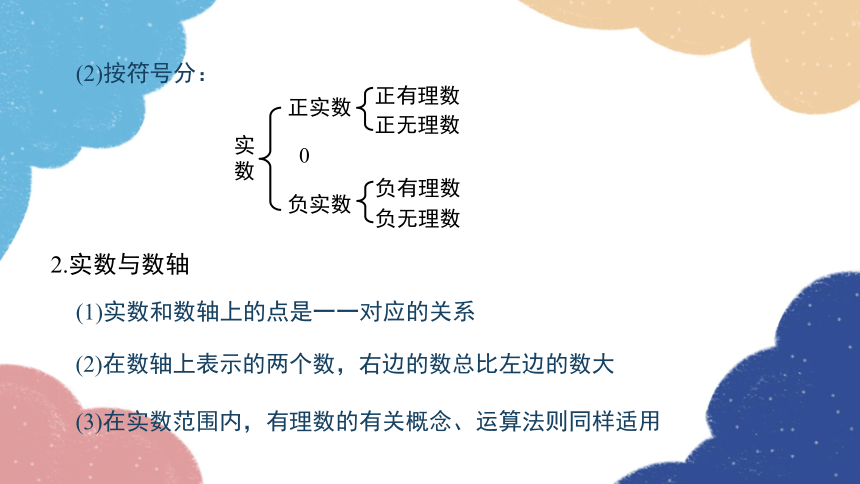
(2)按符号分:
实
数
正实数
负实数
正有理数
正无理数
负有理数
负无理数
0
2.实数与数轴
(1)实数和数轴上的点是一一对应的关系
(2)在数轴上表示的两个数,右边的数总比左边的数大
(3)在实数范围内,有理数的有关概念、运算法则同样适用
例1 已知一个正数的两个平方根分别是a+3和2a-18,求这个正数.
【解析】根据一个正数的平方根有两个,它们互为相反数,可以得到关于a的一元一次方程,解之求得a的值,从而可求出这个正数.
解:根据平方根的性质,有a+3+2a-18=0,解得a=5,a+3=8,82=64,所以这个正数是64.
一个正数的平方根有两个,它们互为相反数.而一个非负数的算术平方根只有一个.另外,一个数的立方根也只有一个,且与它本身的符号相同.
考点讲练
考点一 平方根与立方根
方法总结
B
针对训练
C
-11
1
方法总结
针对训练
C
A
考点二 实数的概念及性质
针对训练
例4 如图所示,数轴上的点A,B分别对应
实数a,b,下列结论正确的是( )
A. a>b B. |a|>|b| C. -ab
a
0
B
A
C
【解析】数轴上的点表示的数,右边的总比左边的大,故A不正确;根据点A,B与原点的距离知|a|<|b|,B不正确;-a>0,根据|a|<|b|,知-a5. 若|a|=-a,则实数a在数轴上的对应点一定在( )
A.原点左侧 B.原点或原点左侧
C.原点右侧 D.原点或原点右侧
B
针对训练
B
【解析】∵4<6<9∴
因此 的值在3到4之间.故选B.
像这类估算无理数的大小的问题,可以将带有根号的无理数的被开方数与已知的平方数作比较,一般的,一个非负数越大,它的算术平方根也越大;也可以利用平方法,将无理数平方后,与已知的平方数作比较.
考点三 实数的计算及估算
方法总结
针对训练
1,0,1
4
【解析】对于被开方数是带分数的二次根式,通常需要先将带分数化成假分数,然后再开方.
故填
8.计算 .
针对训练
课堂小结
有理数
无理数
答 案:
解 析:
答 案:
答 案:
答 案:
81
27
- 13
13
a
∣a∣
a
0
-1、0、1
【解析】只有符号不同的两个数叫做互为相反数,0的相反数为0;一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值;
答 案:
答 案:
答 案:
答 案:
(1)原式 ≈ 4.61;(2)原式 ≈ 9.62
答 案:
答 案:
2、3
答 案:
(1)原式 ≈ 5.873;(2)原式 ≈ 15.708.
答 案:
答 案:
本课结束
第3章 实 数
小结与复习
1. 平方根的概念及性质
2. 算术平方根的概念及性质
(2)性质:正数a有两个平方根,它们互为相反数;
0的平方根是0,负数没有平方根.
(2)性质:0的算术平方根是0,只有非负数才有算术平方根,而且
算术平方根也是非负数.
一、平方根
(1)定义:若r2=a,则r叫作a的一个平方根.
(1)定义:a的正平方根叫作a的算术平方根.
要点梳理
3. 无理数
常见类型: 带根号且开不尽方的数;
含π的一些数;
无限不循环小数.
二、立方根
1. 立方根的概念及性质
(1)定义:如果b3=a,那么b叫作a的立方根.
(2)性质:每一个实数都有一个与它本身符号相同的立方根.
2. 用计算器求立方根
用计算器求一个数a的立方根,其按键顺序为
2ndF
a
=
三、实数
1.实数的分类
(1)按定义分:
实数
有
理
数
分数
整数
无
理
数
(有限小数及
无限循环小数)
(无限不循环小数)
(2)按符号分:
实
数
正实数
负实数
正有理数
正无理数
负有理数
负无理数
0
2.实数与数轴
(1)实数和数轴上的点是一一对应的关系
(2)在数轴上表示的两个数,右边的数总比左边的数大
(3)在实数范围内,有理数的有关概念、运算法则同样适用
例1 已知一个正数的两个平方根分别是a+3和2a-18,求这个正数.
【解析】根据一个正数的平方根有两个,它们互为相反数,可以得到关于a的一元一次方程,解之求得a的值,从而可求出这个正数.
解:根据平方根的性质,有a+3+2a-18=0,解得a=5,a+3=8,82=64,所以这个正数是64.
一个正数的平方根有两个,它们互为相反数.而一个非负数的算术平方根只有一个.另外,一个数的立方根也只有一个,且与它本身的符号相同.
考点讲练
考点一 平方根与立方根
方法总结
B
针对训练
C
-11
1
方法总结
针对训练
C
A
考点二 实数的概念及性质
针对训练
例4 如图所示,数轴上的点A,B分别对应
实数a,b,下列结论正确的是( )
A. a>b B. |a|>|b| C. -ab
a
0
B
A
C
【解析】数轴上的点表示的数,右边的总比左边的大,故A不正确;根据点A,B与原点的距离知|a|<|b|,B不正确;-a>0,根据|a|<|b|,知-a
A.原点左侧 B.原点或原点左侧
C.原点右侧 D.原点或原点右侧
B
针对训练
B
【解析】∵4<6<9∴
因此 的值在3到4之间.故选B.
像这类估算无理数的大小的问题,可以将带有根号的无理数的被开方数与已知的平方数作比较,一般的,一个非负数越大,它的算术平方根也越大;也可以利用平方法,将无理数平方后,与已知的平方数作比较.
考点三 实数的计算及估算
方法总结
针对训练
1,0,1
4
【解析】对于被开方数是带分数的二次根式,通常需要先将带分数化成假分数,然后再开方.
故填
8.计算 .
针对训练
课堂小结
有理数
无理数
答 案:
解 析:
答 案:
答 案:
答 案:
81
27
- 13
13
a
∣a∣
a
0
-1、0、1
【解析】只有符号不同的两个数叫做互为相反数,0的相反数为0;一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值;
答 案:
答 案:
答 案:
答 案:
(1)原式 ≈ 4.61;(2)原式 ≈ 9.62
答 案:
答 案:
2、3
答 案:
(1)原式 ≈ 5.873;(2)原式 ≈ 15.708.
答 案:
答 案:
本课结束
同课章节目录
