3.4 实际问题与一元一次方程(1) 调配问题 课件 (共21张PPT)
文档属性
| 名称 | 3.4 实际问题与一元一次方程(1) 调配问题 课件 (共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-28 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
人教版 七年级上册
3.4实际问题与一元一次方程(1)
调配问题
教学目标:
1 初步掌握建立一元一次方程模型解应用题的方法和步骤.
2 能列出一元一次方程解简单调配、形积类的应用题.
3 让学生在实际生活的问题中感受数学的价值.
教学重点:分析题意,寻找等量关系,设未知数建立方程模型.
教学难点:寻找等量关系.
解方程:
+1
6
=
3
x-2
x
解:去分母
合并同类项,得
移项,得
x-2= 2x+6
系数化为1,得
x-2x=6+2
-x=8.
x=-8.
(方程各项乘以6,约去分母),得
复习旧知
1.解一元一次方程的步骤:
(1)去分母 (2)去括号 (3)移项
(4)合并同类项 (5)系数化为1.
2.解方程的五个步骤在解题时不一定都需要,
可根据题意灵活的选用.
3.去分母时不要忘记添括号,不漏乘不含分母的项.
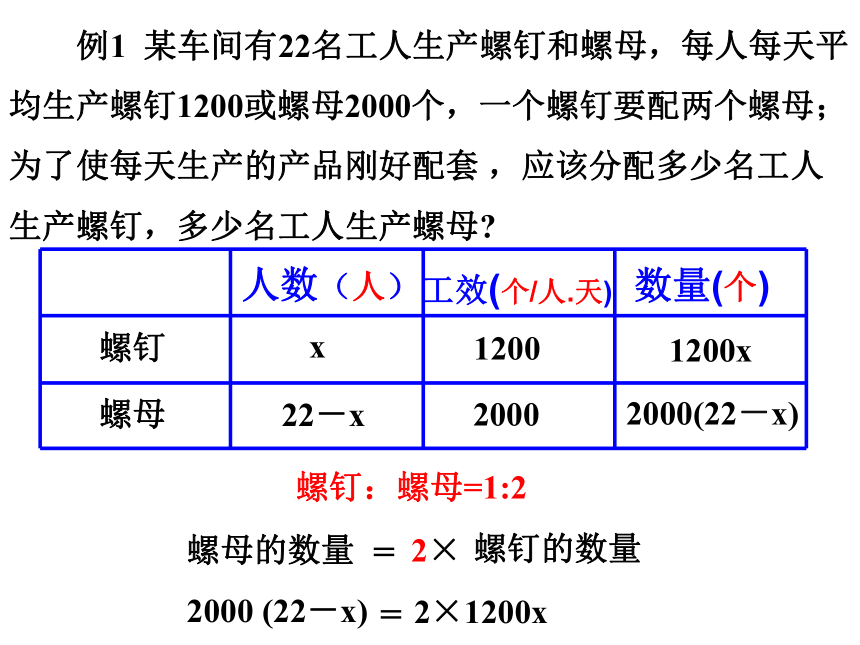
例1 某车间有22名工人生产螺钉和螺母,每人每天平均生产螺钉1200或螺母2000个,一个螺钉要配两个螺母;为了使每天生产的产品刚好配套 ,应该分配多少名工人生产螺钉,多少名工人生产螺母
2000 (22-x)
螺钉
螺母
人数(人)
工效(个/人.天)
数量(个)
x
22-x
1200
2000
1200x
2000(22-x)
螺母的数量
=
2×1200x
螺钉:螺母=1:2
2×
=
螺钉的数量
解:设分配 x名工人生产螺钉,则生产螺母的人数为
(22-x)人.依题意,得:
所以生产螺母的人数为:
答:分配10人生产螺钉,12人生产螺母.可使每天生产的产品刚好配套。
2000 (22-x) = 2×1200x
5 (22 - x) = 6x
110 - 5x = 6x
-11x = -110
x=10.
22-x=1(人).
解方程,得
-5x - 6x = -110
练习1:一套仪器由一个A部件和三个B部件构成。用1方米钢材可做40个A部件或240个B部件。现要用6立
方米钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
A部件
B部件
钢材(m3)
个数(个/m3)
数量(个)
x
6-x
40
240
40x
240 (6-x)
40x
A部件的数量
240 (6-x)
=
B部件的数量
=
3×
A部件:B部件=1:3
3×
解:设应用 x 立方米钢材做A部件,
解方程,得:
x=4
6-x=2
答:
应用4立方米钢材做A部件,2立方米钢材做B部件,恰好配成这种仪器160套.
3×40x= 240(6-x)
40x=40×4=160
(6-x)立方米,
则做B部件的应用,
根据题意,得
x= 2 (6-x)
x= 12-2x
x+2x= 12
3x= 12
练习2:某水利工地派40人去挖土和运土,如果每人 每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?
挖土
运土
人数(人)
工效(方/人.天)
数量(方)
x
40-x
5
3
5x
3 (40-x)
3(40-x)
挖土的数量
运土的数量
=
5x
=
解:设每天派 x 人挖土,
依题意,得:
5x =3 (40-x)
所以每天运土人数为: 40-x=25(人)
x=15
解方程,得:
5x= 120-3x
5x+3x= 120
则每天的运土人数为(40-x)人
答:每天派15人挖土,25人运土,正好能使挖 出的土及时运走.
8x= 120
方法规律:
生产调配问题通常从调配后各量之间的倍、分关系寻找相等关系,建立方程.
例题1:某工厂锻造直径为60毫米,高20毫米的圆柱形零件毛坯,需要截取直径40毫米的圆钢多长?
解:设需要截取直径40毫米的圆钢x毫米,
x= 45
根据题意,得
解方程,得
答:需要截取直径40毫米的圆钢45毫米。
=
202×3.14x
302×3.14
×20
例题2:长方体甲的长、宽、高分别是260毫米,150毫米,325毫米,长方体乙的底面积是130×130毫米2(长、宽都是130毫米).已知甲的体积是乙的体积的2.5倍,求乙的高.
解:设乙长方体的高为x毫米,
x= 150
根据题意,得
解方程,得
答:乙长方体的高为150毫米。
=
2×
130×130x
260×150
×325
方法规律:
等积类问题通常从“变形前的体积=变形后的体积”这个相等关系,建立方程.
1.内径为120毫米的圆柱形玻璃杯,和内径
为300毫米,内高为32毫米的圆柱形玻璃盘可以盛同样多的水,求玻璃杯的内高.
解:设玻璃杯的内高为x毫米,
x= 200
根据题意,得
解方程,得
答:玻璃杯的内高为200毫米。
=
×32
1502×3.14
602×3.14x
练习巩固
2.用内径为90毫米的圆柱形玻璃杯(已装满水)向一个内底面积为131×131毫米2,内高是81毫米的长方体铁盒倒水,当铁盒装满水时,玻璃杯中水的高度下降多少?
解:设玻璃杯的水的高度下降x毫米,
x= 218.6
根据题意,得
解方程,得
答:玻璃杯的水的高度下降218.6毫米。
=
452×3.14x
×81
131×131
3.有一个底面积20×20长方体玻璃杯(已满水)向一个内底面积16×5,内高是10的长方体铁盒倒水,当铁盒装满水时,玻璃杯的水的高度下降多少?
解:设玻璃杯的水的高度下降x个单位,
x= 2
根据题意,得
解方程,得
答:玻璃杯的水的高度下降2单位。
=
20×20x
×10
16×5
4.有9×7×3长方体的蜡烛和棱长为5厘米的正方体蜡烛,现要把这两块蜡烛融化成直径为2厘米的圆柱形蜡烛,问此圆柱形蜡烛有多高?(π≈3.14)
解:设此圆柱形蜡烛的高为xcm,
x=100
根据题意,得
解方程,得
答:此圆柱形蜡烛的高为100cm。
3.14x
=
53
9×7×3
+
今天作业
课本P106页习题第2、3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 七年级上册
3.4实际问题与一元一次方程(1)
调配问题
教学目标:
1 初步掌握建立一元一次方程模型解应用题的方法和步骤.
2 能列出一元一次方程解简单调配、形积类的应用题.
3 让学生在实际生活的问题中感受数学的价值.
教学重点:分析题意,寻找等量关系,设未知数建立方程模型.
教学难点:寻找等量关系.
解方程:
+1
6
=
3
x-2
x
解:去分母
合并同类项,得
移项,得
x-2= 2x+6
系数化为1,得
x-2x=6+2
-x=8.
x=-8.
(方程各项乘以6,约去分母),得
复习旧知
1.解一元一次方程的步骤:
(1)去分母 (2)去括号 (3)移项
(4)合并同类项 (5)系数化为1.
2.解方程的五个步骤在解题时不一定都需要,
可根据题意灵活的选用.
3.去分母时不要忘记添括号,不漏乘不含分母的项.
例1 某车间有22名工人生产螺钉和螺母,每人每天平均生产螺钉1200或螺母2000个,一个螺钉要配两个螺母;为了使每天生产的产品刚好配套 ,应该分配多少名工人生产螺钉,多少名工人生产螺母
2000 (22-x)
螺钉
螺母
人数(人)
工效(个/人.天)
数量(个)
x
22-x
1200
2000
1200x
2000(22-x)
螺母的数量
=
2×1200x
螺钉:螺母=1:2
2×
=
螺钉的数量
解:设分配 x名工人生产螺钉,则生产螺母的人数为
(22-x)人.依题意,得:
所以生产螺母的人数为:
答:分配10人生产螺钉,12人生产螺母.可使每天生产的产品刚好配套。
2000 (22-x) = 2×1200x
5 (22 - x) = 6x
110 - 5x = 6x
-11x = -110
x=10.
22-x=1(人).
解方程,得
-5x - 6x = -110
练习1:一套仪器由一个A部件和三个B部件构成。用1方米钢材可做40个A部件或240个B部件。现要用6立
方米钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
A部件
B部件
钢材(m3)
个数(个/m3)
数量(个)
x
6-x
40
240
40x
240 (6-x)
40x
A部件的数量
240 (6-x)
=
B部件的数量
=
3×
A部件:B部件=1:3
3×
解:设应用 x 立方米钢材做A部件,
解方程,得:
x=4
6-x=2
答:
应用4立方米钢材做A部件,2立方米钢材做B部件,恰好配成这种仪器160套.
3×40x= 240(6-x)
40x=40×4=160
(6-x)立方米,
则做B部件的应用,
根据题意,得
x= 2 (6-x)
x= 12-2x
x+2x= 12
3x= 12
练习2:某水利工地派40人去挖土和运土,如果每人 每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?
挖土
运土
人数(人)
工效(方/人.天)
数量(方)
x
40-x
5
3
5x
3 (40-x)
3(40-x)
挖土的数量
运土的数量
=
5x
=
解:设每天派 x 人挖土,
依题意,得:
5x =3 (40-x)
所以每天运土人数为: 40-x=25(人)
x=15
解方程,得:
5x= 120-3x
5x+3x= 120
则每天的运土人数为(40-x)人
答:每天派15人挖土,25人运土,正好能使挖 出的土及时运走.
8x= 120
方法规律:
生产调配问题通常从调配后各量之间的倍、分关系寻找相等关系,建立方程.
例题1:某工厂锻造直径为60毫米,高20毫米的圆柱形零件毛坯,需要截取直径40毫米的圆钢多长?
解:设需要截取直径40毫米的圆钢x毫米,
x= 45
根据题意,得
解方程,得
答:需要截取直径40毫米的圆钢45毫米。
=
202×3.14x
302×3.14
×20
例题2:长方体甲的长、宽、高分别是260毫米,150毫米,325毫米,长方体乙的底面积是130×130毫米2(长、宽都是130毫米).已知甲的体积是乙的体积的2.5倍,求乙的高.
解:设乙长方体的高为x毫米,
x= 150
根据题意,得
解方程,得
答:乙长方体的高为150毫米。
=
2×
130×130x
260×150
×325
方法规律:
等积类问题通常从“变形前的体积=变形后的体积”这个相等关系,建立方程.
1.内径为120毫米的圆柱形玻璃杯,和内径
为300毫米,内高为32毫米的圆柱形玻璃盘可以盛同样多的水,求玻璃杯的内高.
解:设玻璃杯的内高为x毫米,
x= 200
根据题意,得
解方程,得
答:玻璃杯的内高为200毫米。
=
×32
1502×3.14
602×3.14x
练习巩固
2.用内径为90毫米的圆柱形玻璃杯(已装满水)向一个内底面积为131×131毫米2,内高是81毫米的长方体铁盒倒水,当铁盒装满水时,玻璃杯中水的高度下降多少?
解:设玻璃杯的水的高度下降x毫米,
x= 218.6
根据题意,得
解方程,得
答:玻璃杯的水的高度下降218.6毫米。
=
452×3.14x
×81
131×131
3.有一个底面积20×20长方体玻璃杯(已满水)向一个内底面积16×5,内高是10的长方体铁盒倒水,当铁盒装满水时,玻璃杯的水的高度下降多少?
解:设玻璃杯的水的高度下降x个单位,
x= 2
根据题意,得
解方程,得
答:玻璃杯的水的高度下降2单位。
=
20×20x
×10
16×5
4.有9×7×3长方体的蜡烛和棱长为5厘米的正方体蜡烛,现要把这两块蜡烛融化成直径为2厘米的圆柱形蜡烛,问此圆柱形蜡烛有多高?(π≈3.14)
解:设此圆柱形蜡烛的高为xcm,
x=100
根据题意,得
解方程,得
答:此圆柱形蜡烛的高为100cm。
3.14x
=
53
9×7×3
+
今天作业
课本P106页习题第2、3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
