3.4 实际问题与一元一次方程(2)工程问题 课件(23张PPT)
文档属性
| 名称 | 3.4 实际问题与一元一次方程(2)工程问题 课件(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 10:21:39 | ||
图片预览








文档简介
(共23张PPT)
人教版 七年级上册
3.4实际问题与一元一次方程(2)
工程问题
教学目标:
1 初步掌握建立一元一次方程模型解应用题的方法和步骤.
2 能列出一元一次方程解简单工程类的用题.
3 让学生在实际生活的问题中感受数学的价值.
教学重点:分析题意,寻找等量关系,设未知数建立方程模型.
教学难点:寻找等量关系.
工程问题
1.工作量、工作时间、工作效率;
2.这三个基本量的关系是:
工作量 =工作时间×工作效率
工作效率=工作量÷工作时间
工作时间=工作量÷工作效率
3.工作总量通常看作单位“1”
复习旧知
比一比,赛一赛.
看谁做得好,看谁做得快!
1.一项工作甲独做5天完成,乙独做10天完成,
那么甲每天的工作效率是 ,
乙每天的工作效率是 ,
两人合作1天完成的工作量是 ,
两人合作3天完成的工作量是 .
1
5
1
10
1
5
1
10
+
3( )
1
5
1
10
+
=
9
10
(1)两人合作32小时完成对吗?为什么?
(2)甲每小时完成全部工作的 ;
甲x小时完成全部工作的 ;
乙每小时完成全部工作的 ;
乙x小时完成全部工作的 .
2.一件工作,甲单独做20小时完成,乙单独做
12小时完成.
工程问题中的基本量及其关系:
工作量=工作效率×工作时间
1
20
x
20
1
12
x
12
一个人做1小时完成的工作量是 ;
一个人做4小时完成的工作量是 ;
一个人做x小时完成的工作量是 .
3.整理一块地,由一个人做要80小时完成.
1
80
1
20
x
80
1.在工程问题中,通常把全部工作量简单
的表示为 1.
2.如果一件工作需要n小时完成,那么平均每小时
完成的工作量就是 ,
m 小时完成的工作量就是 .
方法规律:
1
n
m
n
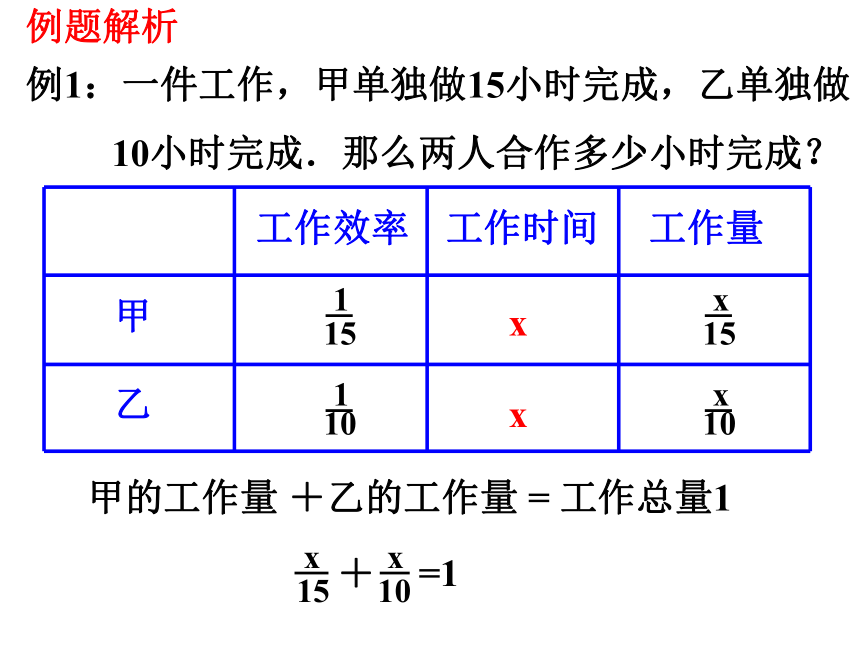
例1:一件工作,甲单独做15小时完成,乙单独做
10小时完成.那么两人合作多少小时完成?
甲
乙
工作效率
工作时间
工作量
x
x
甲的工作量 +乙的工作量 = 工作总量1
x
15
x
10
+
=1
例题解析
1
15
1
10
x
10
x
15
解:设两人合作x小时完成此工作,依题意,得:
答:两人合作6小时完成.
去分母,得
2x+3x=30
合并同类项,得
5x=30
系数化为1,得
x=6
x
15
x
10
+
=1
1.一件工作,甲单独做15小时完成,乙单独做10
小时完成.甲先单独做9小时,后因甲有其它任务调离,
余下的任务由乙单独完成.那么乙还要多少小时完成?
甲
乙
工作效率
工作时间
工作量
9
x
甲的工作量 + 乙的工作量 = 工作总量1
9
15
x
10
+
=1
练习巩固
1
15
1
10
9
15
x
10
答:乙还要4小时完成.
解:设乙还需x小时完成此工作,依题意,得:
3x = 30 - 18
去分母,得
18+3x=30
合并同类项,得
3x=12
系数化为1,得
x=4
移项,得
9
15
x
10
+
=1
2.一件工作,甲单独做15小时完成,乙单独做12小时完成.甲先单独做6小时,然后乙加入 合作,那么两人合作还要多少小时完成?
甲
乙
工作效率
工作时间
工作量
x+6
x
甲的工作量 +乙的工作量 = 工作总量1
x +6
15
x
12
+
=1
1
15
1
12
x
12
x +6
15
答:两人合作还要4小时完成.
解:设两人合作还需x小时完成工作,依题意,得:
4(x+6)+5x=60
4x+24+5x=60
4x + 5x = 60 - 24
9x=36
x=4
去分母,得
合并同类项,得
系数化为1,得
移项,得
去括号,得
x +6
15
x
12
+
=1
(1)人均效率(一个人做一小时的工作量)是 .
(2)这项工作由8人来做,x小时完成的工作量
是 .
总结:一件工作由m个人n小时完成,那么人均
效率是 .
思考:一项工作,12个人4个小时才能完成.
1
12×4
8x
12×4
1
mn
方法总结:
解这类问题常常把总工作量看作1.
工作量=人均效率×人数×时间
例2.整理一批图书,由一个人做要40小时完成.现计划由一部分人先做4小时,然后增加2人与他们一起做8小时,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作
先
后
工作效率
工作时间
工作量
4x
8(x+2)
先做的工作量 + 后做的工作量 = 工作总量1
x人
1
40
1
40
4x
40
8(x +2)
40
解:
设先安排了x人工作4小时.根据题意,得
去分母,得
去括号,得
移项,得
合并,得
系数化为1,得
答:应先安排2名工人工作4小时.
一件工作,甲单独做15小时完成,甲、乙合做6小时完成.甲先单独做6小时,余下的乙单独 做,那么乙还要多少小时完成?
甲
乙
工作效率
工作时间
工作量
6
x
甲的工作量 +乙的工作量 = 工作总量1
练习巩固
答:乙还要6小时完成.
解:设乙还需x小时完成此工作,依题意,得:
去分母,得 12+(5-2)x=30
去括号,得 24+6x=60
移项、合并,得 6x=36
系数化为1,得 x=6
1.在工程问题中,通常把全部工作量简单的表示
为1.如果一件工作需要n小时完成,那么平均
每小时完成的工作量就是 .
2.工作量 = .
3.各阶段工作量的和 = 总工作量
各人完成的工作量的和 = 完成的工作总量
人均效率×人数×时间
课堂小结
1
n
今天作业
课本P106页习题第4、5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 七年级上册
3.4实际问题与一元一次方程(2)
工程问题
教学目标:
1 初步掌握建立一元一次方程模型解应用题的方法和步骤.
2 能列出一元一次方程解简单工程类的用题.
3 让学生在实际生活的问题中感受数学的价值.
教学重点:分析题意,寻找等量关系,设未知数建立方程模型.
教学难点:寻找等量关系.
工程问题
1.工作量、工作时间、工作效率;
2.这三个基本量的关系是:
工作量 =工作时间×工作效率
工作效率=工作量÷工作时间
工作时间=工作量÷工作效率
3.工作总量通常看作单位“1”
复习旧知
比一比,赛一赛.
看谁做得好,看谁做得快!
1.一项工作甲独做5天完成,乙独做10天完成,
那么甲每天的工作效率是 ,
乙每天的工作效率是 ,
两人合作1天完成的工作量是 ,
两人合作3天完成的工作量是 .
1
5
1
10
1
5
1
10
+
3( )
1
5
1
10
+
=
9
10
(1)两人合作32小时完成对吗?为什么?
(2)甲每小时完成全部工作的 ;
甲x小时完成全部工作的 ;
乙每小时完成全部工作的 ;
乙x小时完成全部工作的 .
2.一件工作,甲单独做20小时完成,乙单独做
12小时完成.
工程问题中的基本量及其关系:
工作量=工作效率×工作时间
1
20
x
20
1
12
x
12
一个人做1小时完成的工作量是 ;
一个人做4小时完成的工作量是 ;
一个人做x小时完成的工作量是 .
3.整理一块地,由一个人做要80小时完成.
1
80
1
20
x
80
1.在工程问题中,通常把全部工作量简单
的表示为 1.
2.如果一件工作需要n小时完成,那么平均每小时
完成的工作量就是 ,
m 小时完成的工作量就是 .
方法规律:
1
n
m
n
例1:一件工作,甲单独做15小时完成,乙单独做
10小时完成.那么两人合作多少小时完成?
甲
乙
工作效率
工作时间
工作量
x
x
甲的工作量 +乙的工作量 = 工作总量1
x
15
x
10
+
=1
例题解析
1
15
1
10
x
10
x
15
解:设两人合作x小时完成此工作,依题意,得:
答:两人合作6小时完成.
去分母,得
2x+3x=30
合并同类项,得
5x=30
系数化为1,得
x=6
x
15
x
10
+
=1
1.一件工作,甲单独做15小时完成,乙单独做10
小时完成.甲先单独做9小时,后因甲有其它任务调离,
余下的任务由乙单独完成.那么乙还要多少小时完成?
甲
乙
工作效率
工作时间
工作量
9
x
甲的工作量 + 乙的工作量 = 工作总量1
9
15
x
10
+
=1
练习巩固
1
15
1
10
9
15
x
10
答:乙还要4小时完成.
解:设乙还需x小时完成此工作,依题意,得:
3x = 30 - 18
去分母,得
18+3x=30
合并同类项,得
3x=12
系数化为1,得
x=4
移项,得
9
15
x
10
+
=1
2.一件工作,甲单独做15小时完成,乙单独做12小时完成.甲先单独做6小时,然后乙加入 合作,那么两人合作还要多少小时完成?
甲
乙
工作效率
工作时间
工作量
x+6
x
甲的工作量 +乙的工作量 = 工作总量1
x +6
15
x
12
+
=1
1
15
1
12
x
12
x +6
15
答:两人合作还要4小时完成.
解:设两人合作还需x小时完成工作,依题意,得:
4(x+6)+5x=60
4x+24+5x=60
4x + 5x = 60 - 24
9x=36
x=4
去分母,得
合并同类项,得
系数化为1,得
移项,得
去括号,得
x +6
15
x
12
+
=1
(1)人均效率(一个人做一小时的工作量)是 .
(2)这项工作由8人来做,x小时完成的工作量
是 .
总结:一件工作由m个人n小时完成,那么人均
效率是 .
思考:一项工作,12个人4个小时才能完成.
1
12×4
8x
12×4
1
mn
方法总结:
解这类问题常常把总工作量看作1.
工作量=人均效率×人数×时间
例2.整理一批图书,由一个人做要40小时完成.现计划由一部分人先做4小时,然后增加2人与他们一起做8小时,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作
先
后
工作效率
工作时间
工作量
4x
8(x+2)
先做的工作量 + 后做的工作量 = 工作总量1
x人
1
40
1
40
4x
40
8(x +2)
40
解:
设先安排了x人工作4小时.根据题意,得
去分母,得
去括号,得
移项,得
合并,得
系数化为1,得
答:应先安排2名工人工作4小时.
一件工作,甲单独做15小时完成,甲、乙合做6小时完成.甲先单独做6小时,余下的乙单独 做,那么乙还要多少小时完成?
甲
乙
工作效率
工作时间
工作量
6
x
甲的工作量 +乙的工作量 = 工作总量1
练习巩固
答:乙还要6小时完成.
解:设乙还需x小时完成此工作,依题意,得:
去分母,得 12+(5-2)x=30
去括号,得 24+6x=60
移项、合并,得 6x=36
系数化为1,得 x=6
1.在工程问题中,通常把全部工作量简单的表示
为1.如果一件工作需要n小时完成,那么平均
每小时完成的工作量就是 .
2.工作量 = .
3.各阶段工作量的和 = 总工作量
各人完成的工作量的和 = 完成的工作总量
人均效率×人数×时间
课堂小结
1
n
今天作业
课本P106页习题第4、5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
