冀教版数学六年级上册 第2单元 比和比例-第4课时 比例的基本性质课件(共17张PPT)
文档属性
| 名称 | 冀教版数学六年级上册 第2单元 比和比例-第4课时 比例的基本性质课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-28 11:12:07 | ||
图片预览






文档简介
(共17张PPT)
第4课时 比例的基本性质
第2单元·比和比例
CONTENTS
目录
比 例 的 基 本 性 质
课堂练习
02
新知探究
01
03
课堂小结
新知探究
比 例 的 基 本 性 质
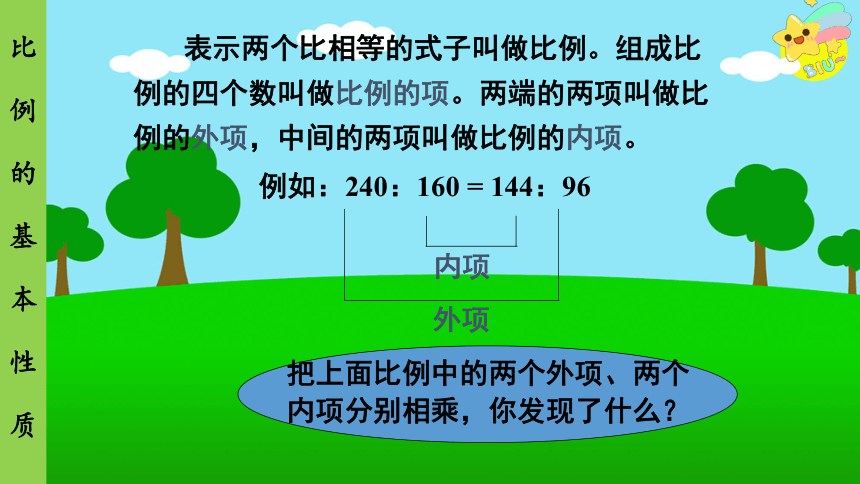
表示两个比相等的式子叫做比例。组成比例的四个数叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
例如:240:160 = 144:96
内项
外项
把上面比例中的两个外项、两个内项分别相乘,你发现了什么?
比 例 的 基 本 性 质
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
如果把比例写成分数形式,等号两端的分子和分母分别交叉相乘,他们的乘积相等。
240 144
160 96
=
比 例 的 基 本 性 质
根据比例的基本性质,如果已知比例中的任何三项,就可以求出另外一个未知项。
求比例中的未知项,叫做解比例。
比 例 的 基 本 性 质
3
课堂练习
比 例 的 基 本 性 质
指出下面比例的外项和内项。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
∶
=
6 ∶4
0.6 ∶0.2
∶
=
外项
外项
内项
内项
外项
内项
外项
内项
比 例 的 基 本 性 质
计算下面比例的外项积和内项积。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
4.5 × 6 = 27
外项积:
内项积:
外项积:
内项积:
2.7 × 10 = 27
6 × 15 = 90
10 × 9 = 90
比 例 的 基 本 性 质
计算下面比例的外项积和内项积。
∶
=
6 ∶4
0.6 ∶0.2
∶
=
外项积:
内项积:
外项积:
内项积:
× 4 = 2
× 6 = 2
0.6 ×
= 0.15
0.2 ×
= 0.15
比 例 的 基 本 性 质
课堂小结
比 例 的 基 本 性 质
1.表示两个比相等的式子叫做比例。组成比例的四个数叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
2.比和比例不同,比表示两个数相除,比例表示两个比相等。
比 例 的 基 本 性 质
3.在比例里,两个外项的积等于两个内项的积。这是比例的基本性质。
4.如果把比例写成分数形式,等号两端的分子和分母分别交叉相乘,它们的积相等。
比 例 的 基 本 性 质
课后作业
2.完成练习册本课时的习题。
1.从课后习题中选取;
谢 谢 观 看
Thanks to watching
第4课时 比例的基本性质
第2单元·比和比例
CONTENTS
目录
比 例 的 基 本 性 质
课堂练习
02
新知探究
01
03
课堂小结
新知探究
比 例 的 基 本 性 质
表示两个比相等的式子叫做比例。组成比例的四个数叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
例如:240:160 = 144:96
内项
外项
把上面比例中的两个外项、两个内项分别相乘,你发现了什么?
比 例 的 基 本 性 质
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
如果把比例写成分数形式,等号两端的分子和分母分别交叉相乘,他们的乘积相等。
240 144
160 96
=
比 例 的 基 本 性 质
根据比例的基本性质,如果已知比例中的任何三项,就可以求出另外一个未知项。
求比例中的未知项,叫做解比例。
比 例 的 基 本 性 质
3
课堂练习
比 例 的 基 本 性 质
指出下面比例的外项和内项。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
∶
=
6 ∶4
0.6 ∶0.2
∶
=
外项
外项
内项
内项
外项
内项
外项
内项
比 例 的 基 本 性 质
计算下面比例的外项积和内项积。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
4.5 × 6 = 27
外项积:
内项积:
外项积:
内项积:
2.7 × 10 = 27
6 × 15 = 90
10 × 9 = 90
比 例 的 基 本 性 质
计算下面比例的外项积和内项积。
∶
=
6 ∶4
0.6 ∶0.2
∶
=
外项积:
内项积:
外项积:
内项积:
× 4 = 2
× 6 = 2
0.6 ×
= 0.15
0.2 ×
= 0.15
比 例 的 基 本 性 质
课堂小结
比 例 的 基 本 性 质
1.表示两个比相等的式子叫做比例。组成比例的四个数叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
2.比和比例不同,比表示两个数相除,比例表示两个比相等。
比 例 的 基 本 性 质
3.在比例里,两个外项的积等于两个内项的积。这是比例的基本性质。
4.如果把比例写成分数形式,等号两端的分子和分母分别交叉相乘,它们的积相等。
比 例 的 基 本 性 质
课后作业
2.完成练习册本课时的习题。
1.从课后习题中选取;
谢 谢 观 看
Thanks to watching
