2022-2023初中数学人教版八上第十二章全等三角形复习精品教案
文档属性
| 名称 | 2022-2023初中数学人教版八上第十二章全等三角形复习精品教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 189.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-28 00:00:00 | ||
图片预览



文档简介
第十二章 全等三角形
知识点一、全等形
1.定义:能够完全重合的两个图形叫作全等形.
2.判定依据:形状相同+大小相等
3.注意:(1)全等形与位置无关,即图形经过平移、翻折、旋转之后所得图形与原图形全等;(2)两个全等形的面积一定相等,但是面积相等的两个图形不一定全等.
知识点二、全等三角形及相关概念
1.定义:能够完全重合的两个三角形叫作全等三角形.
2.对应元素:
(1)对应顶点:全等三角形中,能够重合的顶点.
(2)对应边:全等三角形中,能够重合的边.
(3)对应角:全等三角形中,能够重合的角.
3.表示方法:全等用符号“≌”表示,读作“全等于”.
例如,图12-1中△ABC和△DEF全等,记作≌,读作“△ABC全等于△DEF”,其中点A和点D、点B和点E、点C和点F是对应顶点,AB和DE、AC和DF、BC和EF是对应边,、、是对应角.
图12-1
4.注意:(1)“≌”这种表示方式要求顶点必须严格对应,否则错误;
(2)“△ABC和△DEF全等”这种表示顶点无需严格对应.
知识点三、全等三角形的性质
1.性质:全等三角形的对应边相等,全等三角形的对应角相等
2.书写格式:∵≌,
∴AB=DE,AC=DF,BC=EF;,,.
(注:具体需要写哪几组边角的相等关系,根据具体题目选择即可,不一定全写出来)
3.拓展结论:(1)全等三角形的周长和面积相等;
(2)全等三角形对应边上的中线、高线和对应角的角平分线相等.
4.注意:全等的三角形的性质是可以直接使用的,而拓展结论需要进一步证明才能使用,证
明方式需要根据后续学习全等三角形判定去证明.
知识点四、全等三角形的判定
1.全等三角形的判定方法:
(1) 边角边定理(SAS):两边和它们的夹角对应相等的两个三角形全等.
(2) 角边角定理(ASA):两角和它们的夹边对应相等的两个三角形全等.
(3) 边边边定理(SSS):三边对应相等的两个三角形全等.
(4) 角角边定理(AAS):两个角和其中一个角的对边对应相等的两个三角形全等.
(5) 斜边、直角边定理(HL):斜边和一条直角边对应相等的两个直角三角形全等.
2.特别注意:
(1)“三角相等”即“AAA”不能判定两个三角形全等,例如:常用的30°的直角板的形状相同但是大小可以不同.
(2)“两边及一组等边的对角相等”即“SSA”不能判定两三角形全等,如图12-7:在△ABC和△DEF中可以保证有两组边相等以及一组等边的对角相等,但是两个三角形并不全等.
图12-7
如图,从下列四个条件:①,②,③,
④中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】从题中加上公共角可以得到,同理减去公共角可以得到常考的同角(等角)加减公共角(可记作大角相等小角相等).
一般方法:分别以①、②、③、④作为结论另外三个作为条件来判断正确结论.
②③④得①(SSA)错误;①③④得②(SSA)错误;①②④得③(SSS)正确;①②③得④(SAS)正确.
巧法:四个条件是S、S、S、A只能组成SSS和SAS来判定两三角形全等,从而得到另一个结论,故选B.
【答案】B
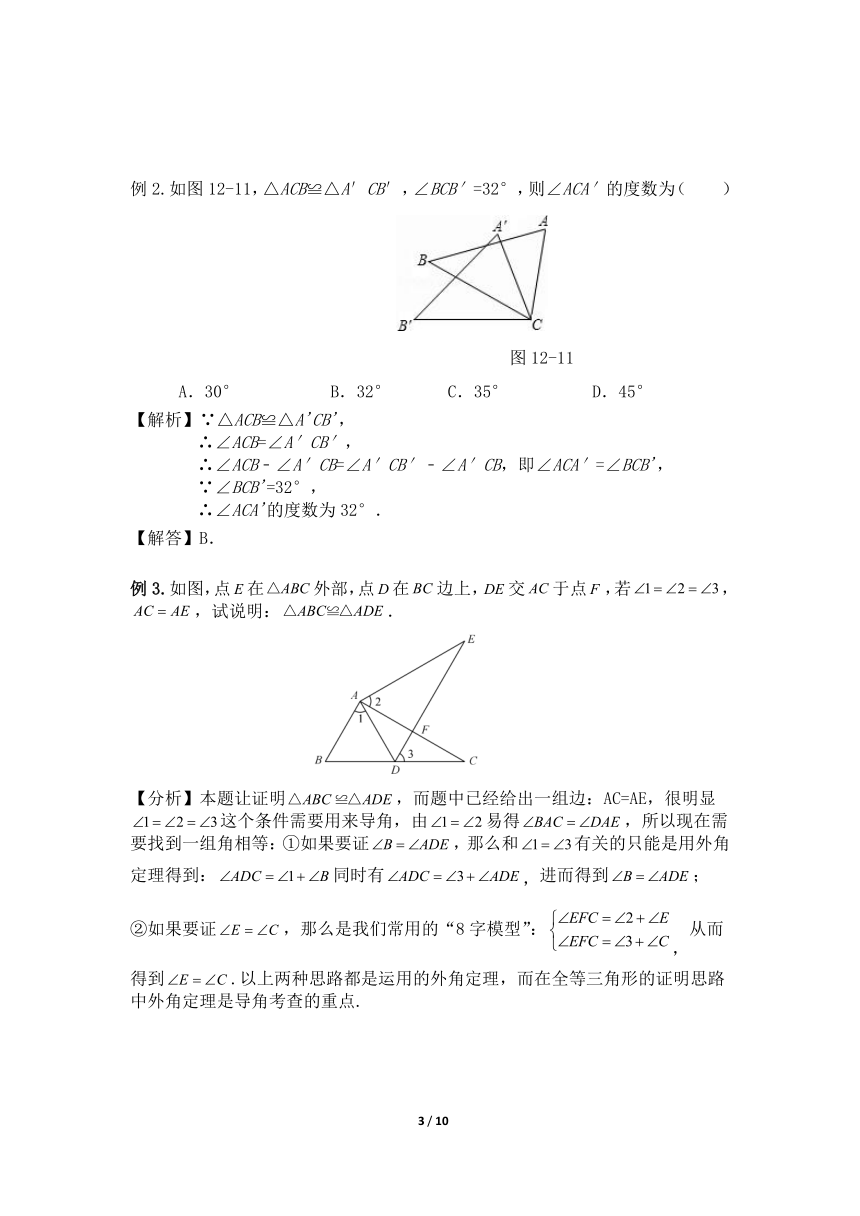
例2.如图12-11,△ACB≌△A′CB′,∠BCB′=32°,则∠ACA′的度数为( )
图12-11
A.30° B.32° C.35° D.45°
【解析】∵△ACB≌△A'CB',
∴∠ACB=∠A′CB′,
∴∠ACB﹣∠A′CB=∠A′CB′﹣∠A′CB,即∠ACA′=∠BCB',
∵∠BCB'=32°,
∴∠ACA'的度数为32°.
【解答】B.
例3.如图,点在外部,点在边上,交于点,若,,试说明:.
【分析】本题让证明,而题中已经给出一组边:AC=AE,很明显这个条件需要用来导角,由易得,所以现在需要找到一组角相等:①如果要证,那么和有关的只能是用外角定理得到:同时有,进而得到;
②如果要证,那么是我们常用的“8字模型”:,从而得到.以上两种思路都是运用的外角定理,而在全等三角形的证明思路中外角定理是导角考查的重点.
【答案】∵,∴,即.
∵,,∴.
在与中
,
∴.
知识点五、全等三角形的基本模型
平移型全等:
此类型的题目一般不会直接说明△ABC平移得到△DEF,需要学生根据图形特点观察出全等三角形,然后进一步利用题中条件进行证明.
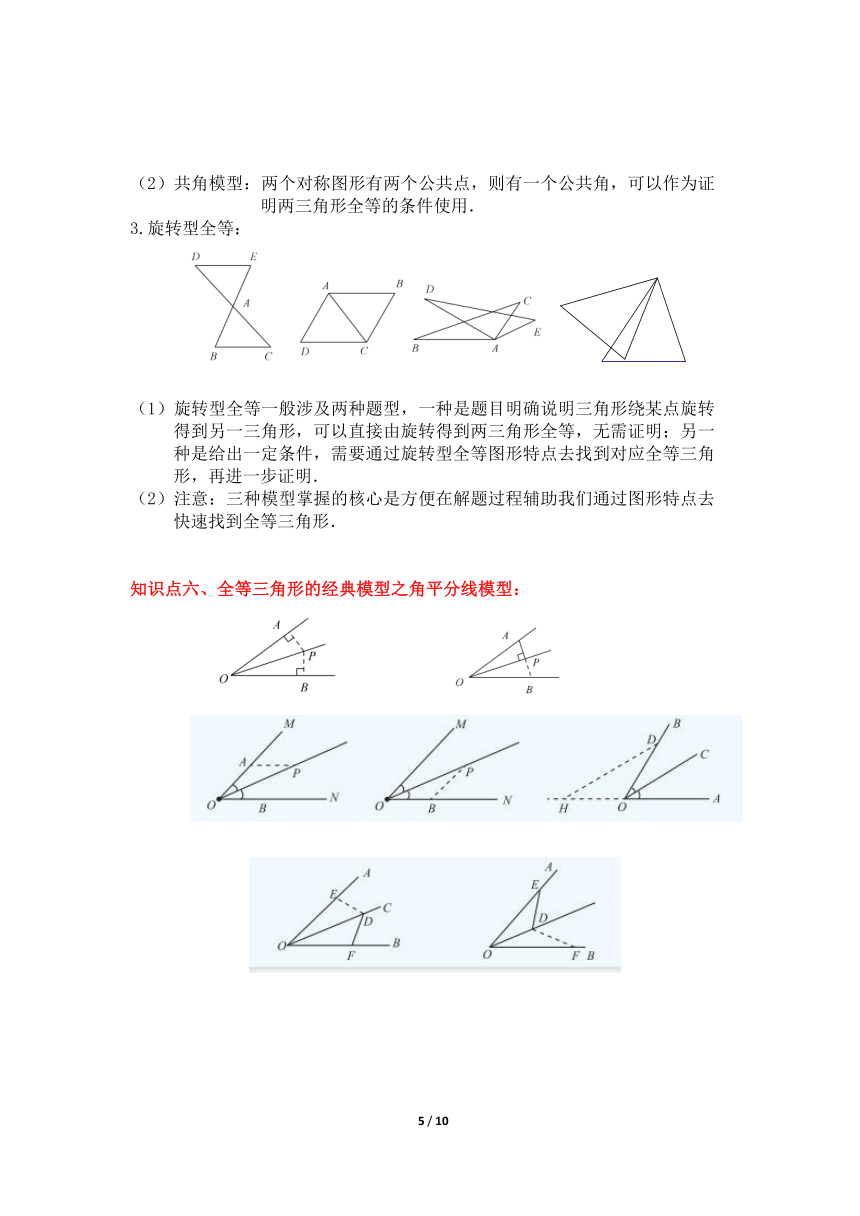
2.对称型全等:
共边模型:两个对称图形有两个公共点,则有一条公共边,可以作为证明两三角形全等的条件使用.
(2)共角模型:两个对称图形有两个公共点,则有一个公共角,可以作为证明两三角形全等的条件使用.
3.旋转型全等:
(1)旋转型全等一般涉及两种题型,一种是题目明确说明三角形绕某点旋转得到另一三角形,可以直接由旋转得到两三角形全等,无需证明;另一种是给出一定条件,需要通过旋转型全等图形特点去找到对应全等三角形,再进一步证明.
(2)注意:三种模型掌握的核心是方便在解题过程辅助我们通过图形特点去快速找到全等三角形.
知识点六、全等三角形的经典模型之角平分线模型:
1.角平分线+外垂直:
此类题型是对于题目中出现角平分线的一般作辅助线思路,可用于角平分线性质使用,也可以用于判定角平分线,所以是考查重中之重.
2.角平分线+内垂直:
此类题型一般会给到一个角平分线的垂直关系如PA⊥OA,只需反向延长PA补出另一个垂直PB即可.其主要作用可以得到△POA≌△POB(ASA).
3.角平分线+平行有等腰三角形:
此类题目会直接给到角平分线和平行关系,如图,OP平分∠AOB,由内错角相等可以得到∠CPO=∠COP,故可以得到△POC为等腰三角形.其主要考查构成的等腰三角形的边角关系.
4.角平分线,分两边----对称全等三角形:
知识点七、角平分线
1.角平分线的尺规作图:作已知角的平分线
作已知角∠AOB的平分线:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;
(2)分别以点M、N为圆心,以大于的长为半径画弧,两弧在∠AOB的
内部交于点C;
(3)作射线OC,射线OC即为∠AOB的平分线.
注意:①整个作图可以得出△OMC和△ONC的三边是相等的,故可以通过全等三角形(SAS)说明OC就是∠AOB的平分线.
②“以大于的长为半径画弧”是由于半径小于两圆弧没有交点.
2.角平分线的性质:
(1)内容:角平分线上的点到角两边的距离相等.
(2)运用及书写格式:
∵OP平分∠AOB,∴PN=PM.
(3)拓展结论:PM=PN(不可直接使用).
(4)注意:此定理证明可以通过AAS证明△PNO≌△PMO得到PM=PN,作为定理可以直接使用,无需再证明全等三角形;角平分线的性质是比全等三角形更快捷的证明线段相等的一种方式.
3.角平分线的判定
(1)内容:角的内部到角的两边的距离相等的点在角平分线上
(2)运用及书写格式:
∵PN=PM
∴OP平分∠AOB
注意:此定理证明可以通过HL证明≌得到,作为定理可以直接使用,无需证明;性质和判定正好条件结论交换,注意区别开;角平分线的判定是比全等三角形更快捷的证明角度相等的一种方式.
例题巩固:
如图,某同学把一块三角形的玻璃打碎了3块,现在要到玻璃店去配一 块完全一样的玻璃,那么最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.带①②③去
【解析】第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.最省事的方法是应带③去,理由是:ASA.
【答案】C.
已知:如图,∠A=∠D=90°,AC=BD.求证:OB=OC.
【解析】由图可以发现其属于对称型中的共边模型,其中BC作为公共边可以作为判定条件使用,由题中∠A=∠D=90°,AC=BD可先通过“HL”判定Rt△BAC≌Rt△CDB.再由要证的结论OB=OC可知需证明△ABO≌△DCO.∵要证明的是两直角三角形斜边相等,∴不能选择“HL”判定,需要由一次全等得到AB=CD,通过“AAS”来判定.在几何证明中注意由条件推出一部分结论和由问题推出一部分要证结论相结合的这种证明思路.
【答案】证明:∵∠A=∠D=90°,
∴△ABC和△DCB是直角三角形
在Rt△BAC和Rt△CDB中,,
∴Rt△BAC≌Rt△CDB(HL).
∴AB=DC.
在△AOB和△DOC中,,
∴△AOB≌△DOC(AAS),
∴OB=OC.
已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是点M、N.试说明:PM=PN.
【解析】根据角平分线的性质以及已知条件证得△ABD≌△CBD(SAS),然后由全等三角形的对应角相等推知∠ADB=∠CDB;再由角平分线性质定理可得PM=PN.
【答案】证明:∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∵PM⊥AD,PN⊥CD,
∴PM=PN.
已知:如图,∠B=∠C=90°,M是BC的中点,且DM平分∠ADC.
(1)求证:AM平分∠DAB;
(2)试说明线段DM与AM有怎样的位置关系?并证明你的结论.
图12-27
【解析】(1)由DM平分∠ADC且已经在AM上有MB⊥AB,∴符合角平分线+外垂直,过M作ME⊥AD于点E,根据角平分线性质求出ME=MC=MB,再根据角平分线判定求出即可;
根据平行线性质求出∠BAD+∠ADC=180°,求出∠MAD+∠MDA=90°,即可求出答案.
【答案】(1)证明:过点M作ME⊥AD于点E,
∵DM平分∠ADC,∠C=90°,ME⊥AD,
∴MC=ME,
∵M为BC的中点,
∴BM=MC=ME,
∵∠B=90°,ME⊥AD,∴AM平分∠DAB;
(2)AM⊥DM.证明如下:
∵AB∥DC,
∴∠BAD+∠ADC=180°,
∵AM平分∠DAB,DM平分∠ADC,
∴∠MAD=∠BAD,∠MDA=∠ADC,
∴∠MAD+∠MDA=90°,
∴∠AMD=90°,
∴AM⊥DM.
2 / 11
知识点一、全等形
1.定义:能够完全重合的两个图形叫作全等形.
2.判定依据:形状相同+大小相等
3.注意:(1)全等形与位置无关,即图形经过平移、翻折、旋转之后所得图形与原图形全等;(2)两个全等形的面积一定相等,但是面积相等的两个图形不一定全等.
知识点二、全等三角形及相关概念
1.定义:能够完全重合的两个三角形叫作全等三角形.
2.对应元素:
(1)对应顶点:全等三角形中,能够重合的顶点.
(2)对应边:全等三角形中,能够重合的边.
(3)对应角:全等三角形中,能够重合的角.
3.表示方法:全等用符号“≌”表示,读作“全等于”.
例如,图12-1中△ABC和△DEF全等,记作≌,读作“△ABC全等于△DEF”,其中点A和点D、点B和点E、点C和点F是对应顶点,AB和DE、AC和DF、BC和EF是对应边,、、是对应角.
图12-1
4.注意:(1)“≌”这种表示方式要求顶点必须严格对应,否则错误;
(2)“△ABC和△DEF全等”这种表示顶点无需严格对应.
知识点三、全等三角形的性质
1.性质:全等三角形的对应边相等,全等三角形的对应角相等
2.书写格式:∵≌,
∴AB=DE,AC=DF,BC=EF;,,.
(注:具体需要写哪几组边角的相等关系,根据具体题目选择即可,不一定全写出来)
3.拓展结论:(1)全等三角形的周长和面积相等;
(2)全等三角形对应边上的中线、高线和对应角的角平分线相等.
4.注意:全等的三角形的性质是可以直接使用的,而拓展结论需要进一步证明才能使用,证
明方式需要根据后续学习全等三角形判定去证明.
知识点四、全等三角形的判定
1.全等三角形的判定方法:
(1) 边角边定理(SAS):两边和它们的夹角对应相等的两个三角形全等.
(2) 角边角定理(ASA):两角和它们的夹边对应相等的两个三角形全等.
(3) 边边边定理(SSS):三边对应相等的两个三角形全等.
(4) 角角边定理(AAS):两个角和其中一个角的对边对应相等的两个三角形全等.
(5) 斜边、直角边定理(HL):斜边和一条直角边对应相等的两个直角三角形全等.
2.特别注意:
(1)“三角相等”即“AAA”不能判定两个三角形全等,例如:常用的30°的直角板的形状相同但是大小可以不同.
(2)“两边及一组等边的对角相等”即“SSA”不能判定两三角形全等,如图12-7:在△ABC和△DEF中可以保证有两组边相等以及一组等边的对角相等,但是两个三角形并不全等.
图12-7
如图,从下列四个条件:①,②,③,
④中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】从题中加上公共角可以得到,同理减去公共角可以得到常考的同角(等角)加减公共角(可记作大角相等小角相等).
一般方法:分别以①、②、③、④作为结论另外三个作为条件来判断正确结论.
②③④得①(SSA)错误;①③④得②(SSA)错误;①②④得③(SSS)正确;①②③得④(SAS)正确.
巧法:四个条件是S、S、S、A只能组成SSS和SAS来判定两三角形全等,从而得到另一个结论,故选B.
【答案】B
例2.如图12-11,△ACB≌△A′CB′,∠BCB′=32°,则∠ACA′的度数为( )
图12-11
A.30° B.32° C.35° D.45°
【解析】∵△ACB≌△A'CB',
∴∠ACB=∠A′CB′,
∴∠ACB﹣∠A′CB=∠A′CB′﹣∠A′CB,即∠ACA′=∠BCB',
∵∠BCB'=32°,
∴∠ACA'的度数为32°.
【解答】B.
例3.如图,点在外部,点在边上,交于点,若,,试说明:.
【分析】本题让证明,而题中已经给出一组边:AC=AE,很明显这个条件需要用来导角,由易得,所以现在需要找到一组角相等:①如果要证,那么和有关的只能是用外角定理得到:同时有,进而得到;
②如果要证,那么是我们常用的“8字模型”:,从而得到.以上两种思路都是运用的外角定理,而在全等三角形的证明思路中外角定理是导角考查的重点.
【答案】∵,∴,即.
∵,,∴.
在与中
,
∴.
知识点五、全等三角形的基本模型
平移型全等:
此类型的题目一般不会直接说明△ABC平移得到△DEF,需要学生根据图形特点观察出全等三角形,然后进一步利用题中条件进行证明.
2.对称型全等:
共边模型:两个对称图形有两个公共点,则有一条公共边,可以作为证明两三角形全等的条件使用.
(2)共角模型:两个对称图形有两个公共点,则有一个公共角,可以作为证明两三角形全等的条件使用.
3.旋转型全等:
(1)旋转型全等一般涉及两种题型,一种是题目明确说明三角形绕某点旋转得到另一三角形,可以直接由旋转得到两三角形全等,无需证明;另一种是给出一定条件,需要通过旋转型全等图形特点去找到对应全等三角形,再进一步证明.
(2)注意:三种模型掌握的核心是方便在解题过程辅助我们通过图形特点去快速找到全等三角形.
知识点六、全等三角形的经典模型之角平分线模型:
1.角平分线+外垂直:
此类题型是对于题目中出现角平分线的一般作辅助线思路,可用于角平分线性质使用,也可以用于判定角平分线,所以是考查重中之重.
2.角平分线+内垂直:
此类题型一般会给到一个角平分线的垂直关系如PA⊥OA,只需反向延长PA补出另一个垂直PB即可.其主要作用可以得到△POA≌△POB(ASA).
3.角平分线+平行有等腰三角形:
此类题目会直接给到角平分线和平行关系,如图,OP平分∠AOB,由内错角相等可以得到∠CPO=∠COP,故可以得到△POC为等腰三角形.其主要考查构成的等腰三角形的边角关系.
4.角平分线,分两边----对称全等三角形:
知识点七、角平分线
1.角平分线的尺规作图:作已知角的平分线
作已知角∠AOB的平分线:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;
(2)分别以点M、N为圆心,以大于的长为半径画弧,两弧在∠AOB的
内部交于点C;
(3)作射线OC,射线OC即为∠AOB的平分线.
注意:①整个作图可以得出△OMC和△ONC的三边是相等的,故可以通过全等三角形(SAS)说明OC就是∠AOB的平分线.
②“以大于的长为半径画弧”是由于半径小于两圆弧没有交点.
2.角平分线的性质:
(1)内容:角平分线上的点到角两边的距离相等.
(2)运用及书写格式:
∵OP平分∠AOB,∴PN=PM.
(3)拓展结论:PM=PN(不可直接使用).
(4)注意:此定理证明可以通过AAS证明△PNO≌△PMO得到PM=PN,作为定理可以直接使用,无需再证明全等三角形;角平分线的性质是比全等三角形更快捷的证明线段相等的一种方式.
3.角平分线的判定
(1)内容:角的内部到角的两边的距离相等的点在角平分线上
(2)运用及书写格式:
∵PN=PM
∴OP平分∠AOB
注意:此定理证明可以通过HL证明≌得到,作为定理可以直接使用,无需证明;性质和判定正好条件结论交换,注意区别开;角平分线的判定是比全等三角形更快捷的证明角度相等的一种方式.
例题巩固:
如图,某同学把一块三角形的玻璃打碎了3块,现在要到玻璃店去配一 块完全一样的玻璃,那么最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.带①②③去
【解析】第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.最省事的方法是应带③去,理由是:ASA.
【答案】C.
已知:如图,∠A=∠D=90°,AC=BD.求证:OB=OC.
【解析】由图可以发现其属于对称型中的共边模型,其中BC作为公共边可以作为判定条件使用,由题中∠A=∠D=90°,AC=BD可先通过“HL”判定Rt△BAC≌Rt△CDB.再由要证的结论OB=OC可知需证明△ABO≌△DCO.∵要证明的是两直角三角形斜边相等,∴不能选择“HL”判定,需要由一次全等得到AB=CD,通过“AAS”来判定.在几何证明中注意由条件推出一部分结论和由问题推出一部分要证结论相结合的这种证明思路.
【答案】证明:∵∠A=∠D=90°,
∴△ABC和△DCB是直角三角形
在Rt△BAC和Rt△CDB中,,
∴Rt△BAC≌Rt△CDB(HL).
∴AB=DC.
在△AOB和△DOC中,,
∴△AOB≌△DOC(AAS),
∴OB=OC.
已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是点M、N.试说明:PM=PN.
【解析】根据角平分线的性质以及已知条件证得△ABD≌△CBD(SAS),然后由全等三角形的对应角相等推知∠ADB=∠CDB;再由角平分线性质定理可得PM=PN.
【答案】证明:∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∵PM⊥AD,PN⊥CD,
∴PM=PN.
已知:如图,∠B=∠C=90°,M是BC的中点,且DM平分∠ADC.
(1)求证:AM平分∠DAB;
(2)试说明线段DM与AM有怎样的位置关系?并证明你的结论.
图12-27
【解析】(1)由DM平分∠ADC且已经在AM上有MB⊥AB,∴符合角平分线+外垂直,过M作ME⊥AD于点E,根据角平分线性质求出ME=MC=MB,再根据角平分线判定求出即可;
根据平行线性质求出∠BAD+∠ADC=180°,求出∠MAD+∠MDA=90°,即可求出答案.
【答案】(1)证明:过点M作ME⊥AD于点E,
∵DM平分∠ADC,∠C=90°,ME⊥AD,
∴MC=ME,
∵M为BC的中点,
∴BM=MC=ME,
∵∠B=90°,ME⊥AD,∴AM平分∠DAB;
(2)AM⊥DM.证明如下:
∵AB∥DC,
∴∠BAD+∠ADC=180°,
∵AM平分∠DAB,DM平分∠ADC,
∴∠MAD=∠BAD,∠MDA=∠ADC,
∴∠MAD+∠MDA=90°,
∴∠AMD=90°,
∴AM⊥DM.
2 / 11
