2022-2023初中数学人教版八上第十三章轴对称复习精品教案
文档属性
| 名称 | 2022-2023初中数学人教版八上第十三章轴对称复习精品教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 104.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-28 15:05:30 | ||
图片预览



文档简介
第十三章 轴对称
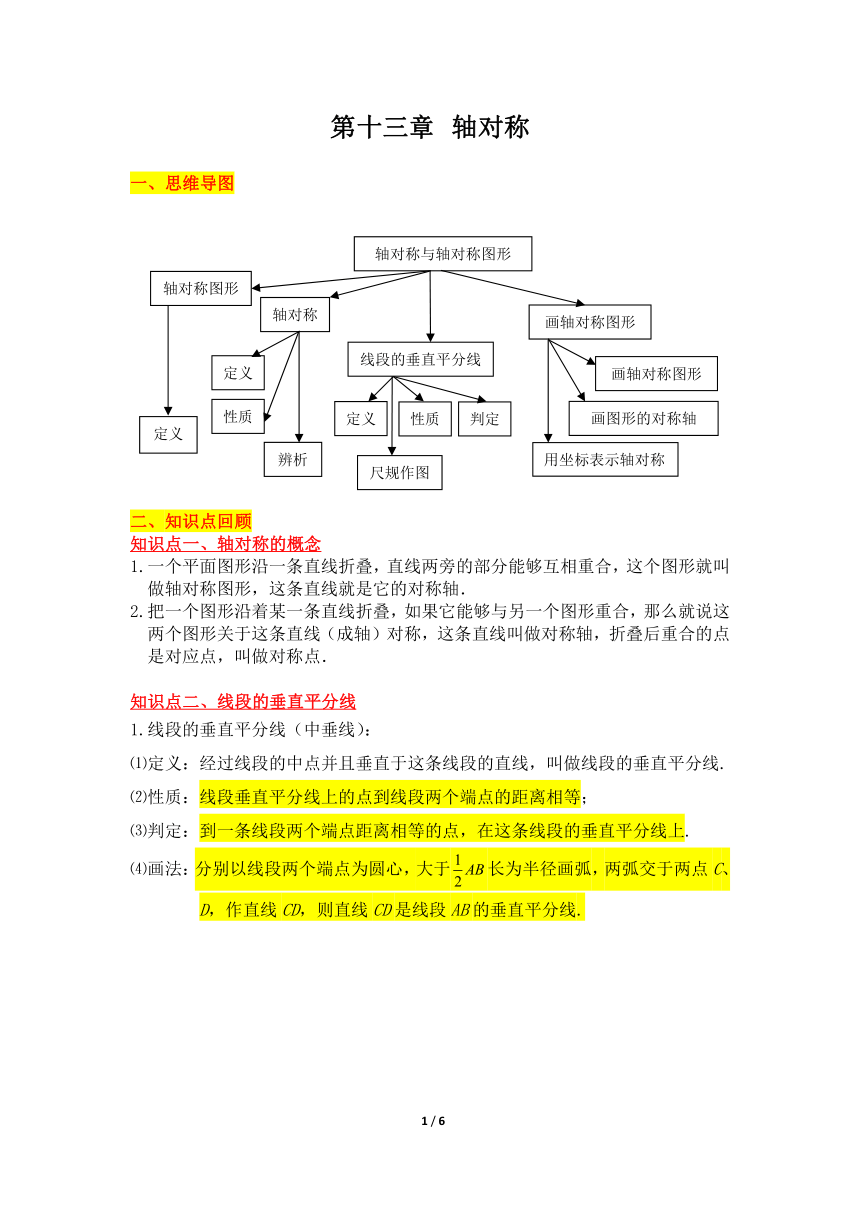
一、思维导图
(
轴对称与轴对称图形
画轴对称图形
画图形的对称轴
轴对称图形
线段的垂直平分线
性质
定义
)
(
轴对称
)
(
画轴对称图形
)
(
性质
) (
判定
) (
尺规作图
)
(
定义
) (
定义
)
(
辨析
) (
用坐标表示轴对称
)
二、知识点回顾
知识点一、轴对称的概念
1.一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
2.把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.
知识点二、线段的垂直平分线
1.线段的垂直平分线(中垂线):
⑴定义:经过线段的中点并且垂直于这条线段的直线,叫做线段的垂直平分线.
⑵性质:线段垂直平分线上的点到线段两个端点的距离相等;
⑶判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
⑷画法:分别以线段两个端点为圆心,大于长为半径画弧,两弧交于两点C、D,作直线CD,则直线CD是线段AB的垂直平分线.
2.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
类似地,轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
对于轴对称图形(或成轴对称的两个图形),找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
例1.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19cm,△ABD的周长为13cm,则AE的长为( )
A.3cm B.6cm C.12cm D.16cm
【分析】根据线段垂直平分线性质得出AD=DC,AE=CE=AC,求出AB+BC+AC=19cm,AB+BD+AD=AB+BC=13cm,即可求出AC,即可得出答案.
【答案】A
知识点三、轴对称
⑴轴对称图形:如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫轴对称图形.这条直线是对称轴.
注:①轴对称图形指的是一个图形,它被对称轴分成的两部分互相重合;
②一个轴对称图形的对称轴不一定只有一条;
③对称轴是一条直线.
⑵轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形完全重合,就说这两个图形关于这条直线对称,这条直线是对称轴,折叠后重合的点是对应点,叫做对称点.
⑶轴对称、轴对称图形的性质:
①关于某条直线对称的两个图形是全等形;
②如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;
③两个图形关于某直线对称,如果他们的对应线段或延长线相交,那么交点在对称轴上;
注:轴对称图形一定是全等形,全等的图形不一定成轴对称.
⑷轴对称图形和两个图形轴对称的区别和联系:
轴对称图形 两个图形轴对称
区别 图形的个数 1个图形 2个图形
对称轴的条数 一条或多条 只有1条
联系 二者都是关于对称轴对称的
知识点四、画轴对称图形
1.轴对称变换:由一个平面图形可以得到与它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全相同;
2.轴对称变换的性质:
(1)新图形上每一点都是原图形上的某一点关于直线l的对称点;
(2)连接任意一对对应点的线段被对称轴垂直平分.
3.画轴对称图形:
(1)找.在原图形上找特殊点;
(2)画.画出图形中特殊点的对称点;
(3)连.连接这些对称点.
4.在平面直角坐标系中,点关于x轴对称的点的坐标为,即横坐标相同,纵坐标互为相反数;
点关于y轴对称的点的坐标为,即纵坐标相同,横坐标互为相反数.
①画某点关于某直线的对称点
过已知点作已知直线(对称轴)的垂线,标出垂足,在这条直线的另一侧从垂足出发在垂线上截取与已知点到垂足的距离相等的线段,截点就是这点关于该直线的对称点.
②画已知图形关于某直线的对称图形
画出图形的某些特殊点关于这条直线的对称点,把这些对称点顺次连接起来,就形成了一个符合条件的对称图形.
③图形对称轴的作法:要作两个图形的对称轴,只要找到这两个图形的一对对应点,然后连接它们,得到一条线段,再作出这条线段的垂直平分线,这条垂直平分线就是这两个图形的对称轴.
3.常见的轴对称图形
⑴线段:两条对称轴,是线段的垂直平分线和线段本身所在直线;
⑵角:一条对称轴,是角平分线所在直线;
⑶圆:无数条对称轴,是经过圆心的直线;
⑷正方形:四条对称轴,对角线所在直线及对边中点连线所在直线;
⑸矩形:两条对称轴,对边中点连线所在直线;
⑹菱形:两条对称轴,对角线所在直线;
⑺等腰三角形:一条对称轴,底边中线(底边高线或顶角平分线)所在直线;
⑻等边三形:三条对称轴,三边中线(高线或内角平分线)所在直线.
例2.已知:如图,及两点,.求作:在平面内找一点,使得,且点到两边所在直线的距离相等.
【答案】因为是两边所在的直线,所以有两个答案.
答案一:内角平分线与线段的垂直平分线的交点,如左图;
答案二:外角平分线与线段的垂直平分线的交点,如右图.
知识点五、等腰三角形
1.等腰三角形的性质:
性质1: 等腰三角形的两个底角相等(简写成“等边对等角”);
如图,在△ABC中,∵AB=AC,∴∠B=∠C.
性质2: 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”).(可用三角形的全等进行证明)
2.等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
知识点六、等边三角形
1.三边都相等的特殊的等腰三角形.
2.等边三角形的三个内角都相等,并且每一个角都等于60°.
3.等边三角形的判定:
(1)三个角都相等的三角形是等边三角形;
(2)有一个角是60°的等腰三角形是等边三角形.
例3..在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
如图,在Rt△ABC中,若∠A=30°,则.
【例2】在平面直角坐标系中,点A坐标为(2,2),点P在x轴上运动,当以点A、P、O为顶点的三角形为等腰三角形时,点P的个数为( )
A.2个 B.3个 C.4个 D.5个
【解答】
如图,当OA=OP时,以O为圆心,AO为半径画圆,可得P1、P2满足条件;
当PA=PO时,作OA的中垂线,可得P3满足条件;
当AO=AP时,以A为圆心,AO为半径画圆,可得P4满足条件.
【答案】C.
2 / 7
一、思维导图
(
轴对称与轴对称图形
画轴对称图形
画图形的对称轴
轴对称图形
线段的垂直平分线
性质
定义
)
(
轴对称
)
(
画轴对称图形
)
(
性质
) (
判定
) (
尺规作图
)
(
定义
) (
定义
)
(
辨析
) (
用坐标表示轴对称
)
二、知识点回顾
知识点一、轴对称的概念
1.一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
2.把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.
知识点二、线段的垂直平分线
1.线段的垂直平分线(中垂线):
⑴定义:经过线段的中点并且垂直于这条线段的直线,叫做线段的垂直平分线.
⑵性质:线段垂直平分线上的点到线段两个端点的距离相等;
⑶判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
⑷画法:分别以线段两个端点为圆心,大于长为半径画弧,两弧交于两点C、D,作直线CD,则直线CD是线段AB的垂直平分线.
2.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
类似地,轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
对于轴对称图形(或成轴对称的两个图形),找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
例1.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19cm,△ABD的周长为13cm,则AE的长为( )
A.3cm B.6cm C.12cm D.16cm
【分析】根据线段垂直平分线性质得出AD=DC,AE=CE=AC,求出AB+BC+AC=19cm,AB+BD+AD=AB+BC=13cm,即可求出AC,即可得出答案.
【答案】A
知识点三、轴对称
⑴轴对称图形:如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫轴对称图形.这条直线是对称轴.
注:①轴对称图形指的是一个图形,它被对称轴分成的两部分互相重合;
②一个轴对称图形的对称轴不一定只有一条;
③对称轴是一条直线.
⑵轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形完全重合,就说这两个图形关于这条直线对称,这条直线是对称轴,折叠后重合的点是对应点,叫做对称点.
⑶轴对称、轴对称图形的性质:
①关于某条直线对称的两个图形是全等形;
②如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;
③两个图形关于某直线对称,如果他们的对应线段或延长线相交,那么交点在对称轴上;
注:轴对称图形一定是全等形,全等的图形不一定成轴对称.
⑷轴对称图形和两个图形轴对称的区别和联系:
轴对称图形 两个图形轴对称
区别 图形的个数 1个图形 2个图形
对称轴的条数 一条或多条 只有1条
联系 二者都是关于对称轴对称的
知识点四、画轴对称图形
1.轴对称变换:由一个平面图形可以得到与它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全相同;
2.轴对称变换的性质:
(1)新图形上每一点都是原图形上的某一点关于直线l的对称点;
(2)连接任意一对对应点的线段被对称轴垂直平分.
3.画轴对称图形:
(1)找.在原图形上找特殊点;
(2)画.画出图形中特殊点的对称点;
(3)连.连接这些对称点.
4.在平面直角坐标系中,点关于x轴对称的点的坐标为,即横坐标相同,纵坐标互为相反数;
点关于y轴对称的点的坐标为,即纵坐标相同,横坐标互为相反数.
①画某点关于某直线的对称点
过已知点作已知直线(对称轴)的垂线,标出垂足,在这条直线的另一侧从垂足出发在垂线上截取与已知点到垂足的距离相等的线段,截点就是这点关于该直线的对称点.
②画已知图形关于某直线的对称图形
画出图形的某些特殊点关于这条直线的对称点,把这些对称点顺次连接起来,就形成了一个符合条件的对称图形.
③图形对称轴的作法:要作两个图形的对称轴,只要找到这两个图形的一对对应点,然后连接它们,得到一条线段,再作出这条线段的垂直平分线,这条垂直平分线就是这两个图形的对称轴.
3.常见的轴对称图形
⑴线段:两条对称轴,是线段的垂直平分线和线段本身所在直线;
⑵角:一条对称轴,是角平分线所在直线;
⑶圆:无数条对称轴,是经过圆心的直线;
⑷正方形:四条对称轴,对角线所在直线及对边中点连线所在直线;
⑸矩形:两条对称轴,对边中点连线所在直线;
⑹菱形:两条对称轴,对角线所在直线;
⑺等腰三角形:一条对称轴,底边中线(底边高线或顶角平分线)所在直线;
⑻等边三形:三条对称轴,三边中线(高线或内角平分线)所在直线.
例2.已知:如图,及两点,.求作:在平面内找一点,使得,且点到两边所在直线的距离相等.
【答案】因为是两边所在的直线,所以有两个答案.
答案一:内角平分线与线段的垂直平分线的交点,如左图;
答案二:外角平分线与线段的垂直平分线的交点,如右图.
知识点五、等腰三角形
1.等腰三角形的性质:
性质1: 等腰三角形的两个底角相等(简写成“等边对等角”);
如图,在△ABC中,∵AB=AC,∴∠B=∠C.
性质2: 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”).(可用三角形的全等进行证明)
2.等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
知识点六、等边三角形
1.三边都相等的特殊的等腰三角形.
2.等边三角形的三个内角都相等,并且每一个角都等于60°.
3.等边三角形的判定:
(1)三个角都相等的三角形是等边三角形;
(2)有一个角是60°的等腰三角形是等边三角形.
例3..在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
如图,在Rt△ABC中,若∠A=30°,则.
【例2】在平面直角坐标系中,点A坐标为(2,2),点P在x轴上运动,当以点A、P、O为顶点的三角形为等腰三角形时,点P的个数为( )
A.2个 B.3个 C.4个 D.5个
【解答】
如图,当OA=OP时,以O为圆心,AO为半径画圆,可得P1、P2满足条件;
当PA=PO时,作OA的中垂线,可得P3满足条件;
当AO=AP时,以A为圆心,AO为半径画圆,可得P4满足条件.
【答案】C.
2 / 7
