23.1 锐角三角函数 (2) 课件(25张PPT)
文档属性
| 名称 | 23.1 锐角三角函数 (2) 课件(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
沪科版 九年级上册
23.1 锐角三角函数 (2)
教学目标
1.联系生活实际,经历探索直角三角形中边角关系的过程,了解当锐角固定时,它的对边(邻边),斜边中两边比值也是固定不变的,初步理解角度与数值(比值)之间的一一对应关系.
2.了解直角三角形中锐角三角函数的概念,能正确运用sinA、sosA表示直角三角形(锐角)中对边与斜边的比、邻边与斜边的比.
3.根据三角形边角关系,能够由给出的边长求sinA和cosA.
教学重点:锐角的正弦函数和余弦函数的概念.
教学难点:锐角的正弦函数和余弦函数的概念.
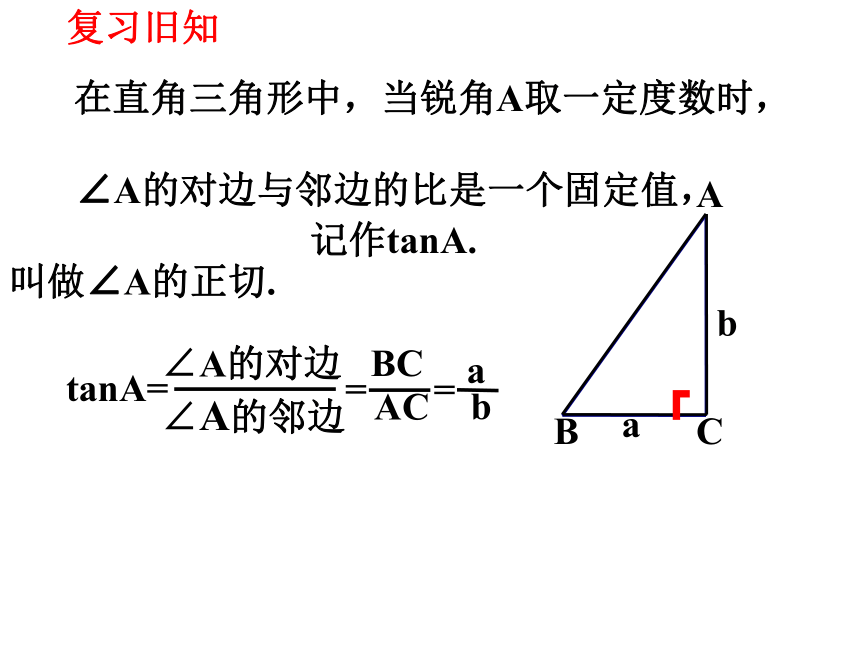
在直角三角形中,当锐角A取一定度数时,
∠A的对边与邻边的比是一个固定值,
叫做∠A的正切.
B
C
A
┏
=
tanA=
∠A的邻边
∠A的对边
BC
AC
=
a
b
a
b
记作tanA.
复习旧知
B
C
A
┏
B1
B2
C1
C2
┏
┏
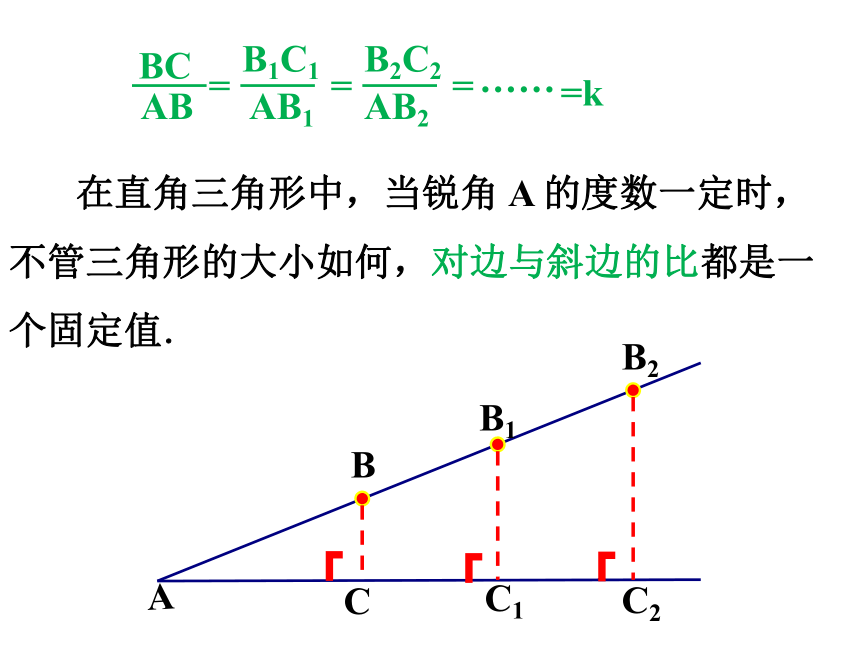
Rt△ABC∽Rt△A1B1 C1∽Rt△A2B2 C2 ……
在直角三角形中,锐角 A 的对边与斜边的比
AB
BC
,
AB1
B1C1
,
AB2
B2C2
,
……,
关系怎样?
AB
BC
=
AB1
B1C1
=
AB2
B2C2
=
……
=k
B
C
A
┏
B1
B2
C1
C2
┏
┏
在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,对边与斜边的比都是一个固定值.
AB
BC
=
AB1
B1C1
=
AB2
B2C2
=
……
=k
在直角三角形中,当锐角A取一定度数时,
∠A的对边与斜边的比是一个固定值,
叫做∠A的正弦.
B
C
A
┏
=
sinA=
斜边
∠A的对边
BC
AB
=
a
c
a
b
记作sinA.
c
B
C
A
┏
B1
B2
C1
C2
┏
┏
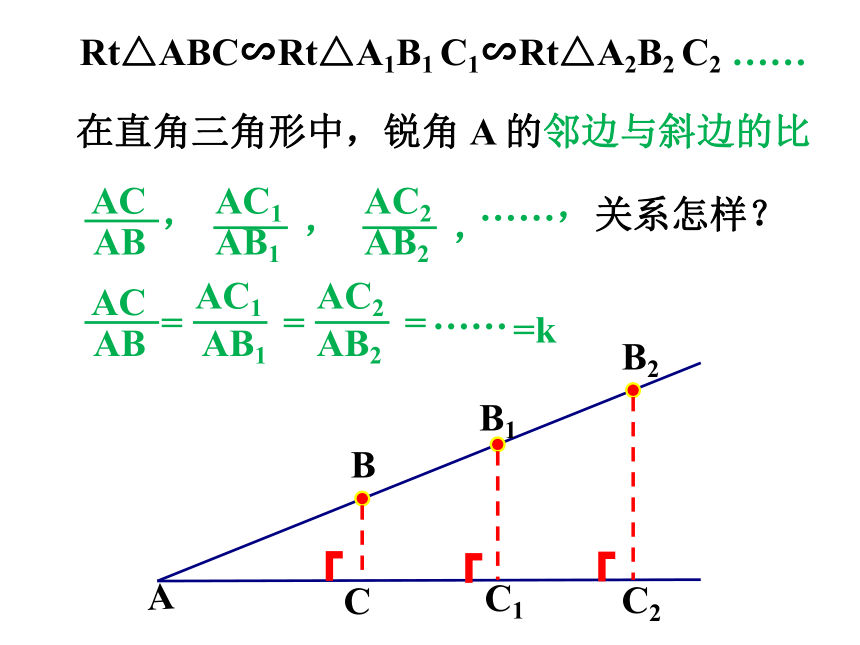
Rt△ABC∽Rt△A1B1 C1∽Rt△A2B2 C2 ……
在直角三角形中,锐角 A 的邻边与斜边的比
AB
AC
,
AB1
AC1
,
AB2
AC2
,
……,
关系怎样?
AB
AC
=
AB1
AC1
=
AB2
AC2
=
……
=k
B
C
A
┏
B1
B2
C1
C2
┏
┏
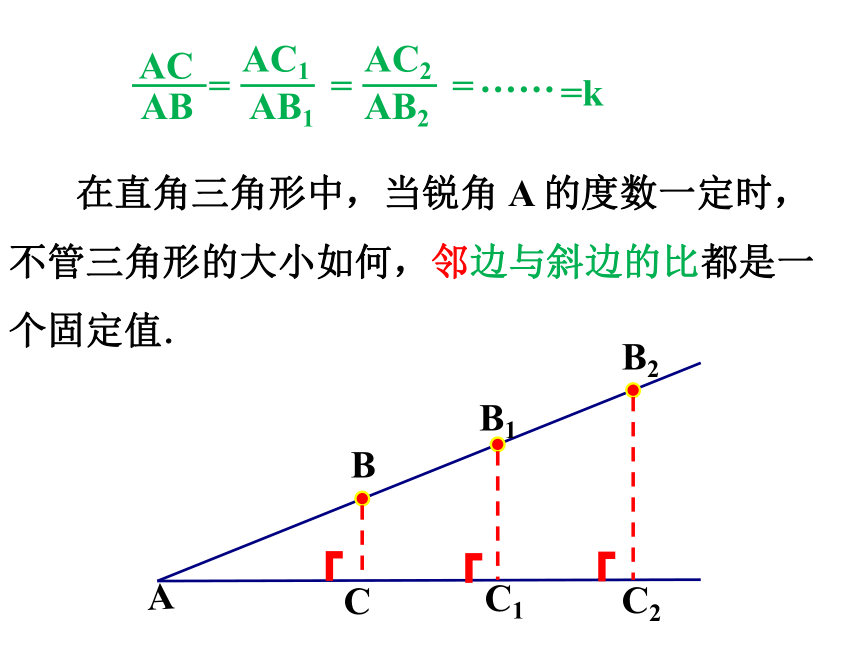
在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,邻边与斜边的比都是一个固定值.
AB
AC
=
AB1
AC1
=
AB2
AC2
=
……
=k
在直角三角形中,当锐角A取一定度数时,
∠A的邻边与斜边的比是一个固定值,
叫做∠A的余弦.
B
C
A
┏
=
cosA=
斜边
∠A的邻边
AC
AB
=
b
c
a
b
记作cosA.
c
B
a
C
b
A
c
┏
∠A的对边
斜边
∠A的对边
=
a
c
=
=
sinA=
BC
AB
=
cosA=
斜边
∠A的邻边
AC
AB
=
b
c
tanA=
∠A的邻边
∠A的对边
BC
AC
=
a
b
∠A的邻边
锐角A的正弦、余弦、和正切叫做∠A的锐角三角函数.
B
a
C
b
A
c
┏
∠B的对边
斜边
∠B的对边
=
b
c
=
=
sinB=
AC
AB
=
cosB=
斜边
∠B的邻边
=
a
c
tanB=
∠B的邻边
∠B的对边
=
b
a
∠B的邻边
写出锐角B的正弦、余弦、和正切.
BC
AB
AC
BC
锐角三角函数中应该注意的几个问题:
1.sinA,cosA,tanA, 是在直角三角形中定义的, ∠A是
锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA,是一个完整的符号, 习惯省去
“∠”号;
3.sinA,cosA,tanA,是一个比值.注意比的顺序,
且sinA,cosA,tanA, 均大于0,无单位.
4.sinA,cosA,tanA, 的大小只与∠A的大小有关,
而与直角三角形的边长无关.
B
a
C
b
A
c
┏
直角三角形边与角的关系
a称为∠A的对边,
b称为∠A的邻边,
∠A与边的关系:
斜边
∠A的对边
=
a
c
斜边
∠A的对边
=
a
c
斜边
∠A的邻边
=
b
c
斜边
∠A的邻边
=
c
b
∠A的邻边
∠A的对边
=
a
b
∠A的邻边
∠A的对边
=
a
b
例2 如图,在Rt△ABC中,∠C=90°,两直角边AC=12,BC=5,求∠A的各个三角函数.
A
B
C
5
12
解:在Rt△ABC中,
∵∠C=90°,AC=12,BC=5,
∴AB=13.
∴ sinA=
=
5
13
cosA=
AC
AB
=
12
13
tanA=
5
12
∴AB2=AC2+BC2=122+52=132,
BC
AB
BC
AC
=
1.如图,在△ABC中,∠C=90°,AB=10, AC=6,
求sinA、cosA、tanA、sinB、cosB、tanB.
解:
B
A
C
∵∠C=90°,AB=10,AC=6,
∴BC2=AB2-AC2=102-62=82,
∴BC=8.
∴ sinA=
=
8
10
BC
AB
=
4
5
cosA=
=
6
10
AC
AB
=
3
5
tanA=
=
8
6
BC
AC
=
4
3
sinB=
=
6
10
AC
AB
=
3
5
cosB=
=
8
10
BC
AB
=
4
5
tanB=
=
6
8
AC
BC
=
3
4
练习巩固
2.如图,在△ABC中,∠C=90°,BC=4, AC=8,
CD⊥AB,求sin∠ACD、cos∠BCD.
∴ sin∠ACD=sinB
=
AC
AB
=
5
cosA=
=
AC
AB
∵∠C=90°,BC=4,AC=8,
∴AB2=AC2+BC2=42+82=80,
∴AB=4 .
解:
5
∵CD⊥AB,
∴∠CDA=∠CDB=90°
∴∠ACD=∠B,
∠BCD=∠A,
=
4
5
8
cos∠BCD=
=
5
4
5
8
2
5
D
2
5
B
A
C
3. 在平面直角坐标系内有一点P( 3,4),连接OP,
求OP与x轴正方向所夹锐角α的各个三角函数.
x
y
O
P( 3,4)
α
Q
∵点P的坐标为( 3,4)
解:
∴OQ=3,
PQ=4,
∴OP2=OQ2+PQ2
∴OP=5 .
=32+42=25,
∴ sinα
PQ
OP
=
cosα=
=
OQ
OP
tanα=
=
4
3
PQ
OQ
3
5
=
4
5
过点P作PQ⊥x轴,垂足为Q,
4. 在平面直角坐标系内有一点P( 2,5),连接OP,
求OP与x轴正方向所夹锐角α的各个三角函数.
x
y
O
P( 2,5)
α
D
∵点P的坐标为( 2,5)
解:
∴OD=2,
PD=5,
∴OP2=OD2+PD2
∴OP= .
29
=22+52=29,
∴ sinα
=
PD
OP
=
29
=
29
5
29
5
cosα=
=
OD
OP
=
29
29
2
2
29
tanα=
=
5
2
PD
OD
5. 菱形ABCD的两条对角线分别为AC=8cm,
BD=6cm,求tan∠BAC.
A
B
C
D
O
∵ AC、BD为菱形ABCD的两条对角线
∴AC⊥BD,
∴∠AOB=90°
AO= AC=4,
BO= BD=3,
BO
AO
∴tan∠BAC=
=
3
4
1
2
1
2
解:
6.在△ABC中,∠C=90°,sinA= ,
求cosA.
3
5
A
B
C
解:
∵ ∠C=90°, sinA= ,
3
5
sinA=
BC
AB
∴ =
BC
AB
3
5
设BC=3k,
则AB=5k,
∴ AC=4k.
∴ cosA=
AC
AB
=
4k
5k
=
4
5
1.将∠AOB放在5×5的正方形方格中,则cos∠ADB值是 .
巩固提高
13
2
13
2.在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若AC= ,BC=2,则sin∠ACD等于( ).
A. B. C. D.
3
2
5
2
5
3
5
3
2
C
A
B
C
2
D
今天作业
课本P116页第3、4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
23.1 锐角三角函数 (2)
教学目标
1.联系生活实际,经历探索直角三角形中边角关系的过程,了解当锐角固定时,它的对边(邻边),斜边中两边比值也是固定不变的,初步理解角度与数值(比值)之间的一一对应关系.
2.了解直角三角形中锐角三角函数的概念,能正确运用sinA、sosA表示直角三角形(锐角)中对边与斜边的比、邻边与斜边的比.
3.根据三角形边角关系,能够由给出的边长求sinA和cosA.
教学重点:锐角的正弦函数和余弦函数的概念.
教学难点:锐角的正弦函数和余弦函数的概念.
在直角三角形中,当锐角A取一定度数时,
∠A的对边与邻边的比是一个固定值,
叫做∠A的正切.
B
C
A
┏
=
tanA=
∠A的邻边
∠A的对边
BC
AC
=
a
b
a
b
记作tanA.
复习旧知
B
C
A
┏
B1
B2
C1
C2
┏
┏
Rt△ABC∽Rt△A1B1 C1∽Rt△A2B2 C2 ……
在直角三角形中,锐角 A 的对边与斜边的比
AB
BC
,
AB1
B1C1
,
AB2
B2C2
,
……,
关系怎样?
AB
BC
=
AB1
B1C1
=
AB2
B2C2
=
……
=k
B
C
A
┏
B1
B2
C1
C2
┏
┏
在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,对边与斜边的比都是一个固定值.
AB
BC
=
AB1
B1C1
=
AB2
B2C2
=
……
=k
在直角三角形中,当锐角A取一定度数时,
∠A的对边与斜边的比是一个固定值,
叫做∠A的正弦.
B
C
A
┏
=
sinA=
斜边
∠A的对边
BC
AB
=
a
c
a
b
记作sinA.
c
B
C
A
┏
B1
B2
C1
C2
┏
┏
Rt△ABC∽Rt△A1B1 C1∽Rt△A2B2 C2 ……
在直角三角形中,锐角 A 的邻边与斜边的比
AB
AC
,
AB1
AC1
,
AB2
AC2
,
……,
关系怎样?
AB
AC
=
AB1
AC1
=
AB2
AC2
=
……
=k
B
C
A
┏
B1
B2
C1
C2
┏
┏
在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,邻边与斜边的比都是一个固定值.
AB
AC
=
AB1
AC1
=
AB2
AC2
=
……
=k
在直角三角形中,当锐角A取一定度数时,
∠A的邻边与斜边的比是一个固定值,
叫做∠A的余弦.
B
C
A
┏
=
cosA=
斜边
∠A的邻边
AC
AB
=
b
c
a
b
记作cosA.
c
B
a
C
b
A
c
┏
∠A的对边
斜边
∠A的对边
=
a
c
=
=
sinA=
BC
AB
=
cosA=
斜边
∠A的邻边
AC
AB
=
b
c
tanA=
∠A的邻边
∠A的对边
BC
AC
=
a
b
∠A的邻边
锐角A的正弦、余弦、和正切叫做∠A的锐角三角函数.
B
a
C
b
A
c
┏
∠B的对边
斜边
∠B的对边
=
b
c
=
=
sinB=
AC
AB
=
cosB=
斜边
∠B的邻边
=
a
c
tanB=
∠B的邻边
∠B的对边
=
b
a
∠B的邻边
写出锐角B的正弦、余弦、和正切.
BC
AB
AC
BC
锐角三角函数中应该注意的几个问题:
1.sinA,cosA,tanA, 是在直角三角形中定义的, ∠A是
锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA,是一个完整的符号, 习惯省去
“∠”号;
3.sinA,cosA,tanA,是一个比值.注意比的顺序,
且sinA,cosA,tanA, 均大于0,无单位.
4.sinA,cosA,tanA, 的大小只与∠A的大小有关,
而与直角三角形的边长无关.
B
a
C
b
A
c
┏
直角三角形边与角的关系
a称为∠A的对边,
b称为∠A的邻边,
∠A与边的关系:
斜边
∠A的对边
=
a
c
斜边
∠A的对边
=
a
c
斜边
∠A的邻边
=
b
c
斜边
∠A的邻边
=
c
b
∠A的邻边
∠A的对边
=
a
b
∠A的邻边
∠A的对边
=
a
b
例2 如图,在Rt△ABC中,∠C=90°,两直角边AC=12,BC=5,求∠A的各个三角函数.
A
B
C
5
12
解:在Rt△ABC中,
∵∠C=90°,AC=12,BC=5,
∴AB=13.
∴ sinA=
=
5
13
cosA=
AC
AB
=
12
13
tanA=
5
12
∴AB2=AC2+BC2=122+52=132,
BC
AB
BC
AC
=
1.如图,在△ABC中,∠C=90°,AB=10, AC=6,
求sinA、cosA、tanA、sinB、cosB、tanB.
解:
B
A
C
∵∠C=90°,AB=10,AC=6,
∴BC2=AB2-AC2=102-62=82,
∴BC=8.
∴ sinA=
=
8
10
BC
AB
=
4
5
cosA=
=
6
10
AC
AB
=
3
5
tanA=
=
8
6
BC
AC
=
4
3
sinB=
=
6
10
AC
AB
=
3
5
cosB=
=
8
10
BC
AB
=
4
5
tanB=
=
6
8
AC
BC
=
3
4
练习巩固
2.如图,在△ABC中,∠C=90°,BC=4, AC=8,
CD⊥AB,求sin∠ACD、cos∠BCD.
∴ sin∠ACD=sinB
=
AC
AB
=
5
cosA=
=
AC
AB
∵∠C=90°,BC=4,AC=8,
∴AB2=AC2+BC2=42+82=80,
∴AB=4 .
解:
5
∵CD⊥AB,
∴∠CDA=∠CDB=90°
∴∠ACD=∠B,
∠BCD=∠A,
=
4
5
8
cos∠BCD=
=
5
4
5
8
2
5
D
2
5
B
A
C
3. 在平面直角坐标系内有一点P( 3,4),连接OP,
求OP与x轴正方向所夹锐角α的各个三角函数.
x
y
O
P( 3,4)
α
Q
∵点P的坐标为( 3,4)
解:
∴OQ=3,
PQ=4,
∴OP2=OQ2+PQ2
∴OP=5 .
=32+42=25,
∴ sinα
PQ
OP
=
cosα=
=
OQ
OP
tanα=
=
4
3
PQ
OQ
3
5
=
4
5
过点P作PQ⊥x轴,垂足为Q,
4. 在平面直角坐标系内有一点P( 2,5),连接OP,
求OP与x轴正方向所夹锐角α的各个三角函数.
x
y
O
P( 2,5)
α
D
∵点P的坐标为( 2,5)
解:
∴OD=2,
PD=5,
∴OP2=OD2+PD2
∴OP= .
29
=22+52=29,
∴ sinα
=
PD
OP
=
29
=
29
5
29
5
cosα=
=
OD
OP
=
29
29
2
2
29
tanα=
=
5
2
PD
OD
5. 菱形ABCD的两条对角线分别为AC=8cm,
BD=6cm,求tan∠BAC.
A
B
C
D
O
∵ AC、BD为菱形ABCD的两条对角线
∴AC⊥BD,
∴∠AOB=90°
AO= AC=4,
BO= BD=3,
BO
AO
∴tan∠BAC=
=
3
4
1
2
1
2
解:
6.在△ABC中,∠C=90°,sinA= ,
求cosA.
3
5
A
B
C
解:
∵ ∠C=90°, sinA= ,
3
5
sinA=
BC
AB
∴ =
BC
AB
3
5
设BC=3k,
则AB=5k,
∴ AC=4k.
∴ cosA=
AC
AB
=
4k
5k
=
4
5
1.将∠AOB放在5×5的正方形方格中,则cos∠ADB值是 .
巩固提高
13
2
13
2.在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若AC= ,BC=2,则sin∠ACD等于( ).
A. B. C. D.
3
2
5
2
5
3
5
3
2
C
A
B
C
2
D
今天作业
课本P116页第3、4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
