23.1 锐角三角函数 (3) 课件(23张PPT)
文档属性
| 名称 | 23.1 锐角三角函数 (3) 课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1006.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 10:42:33 | ||
图片预览


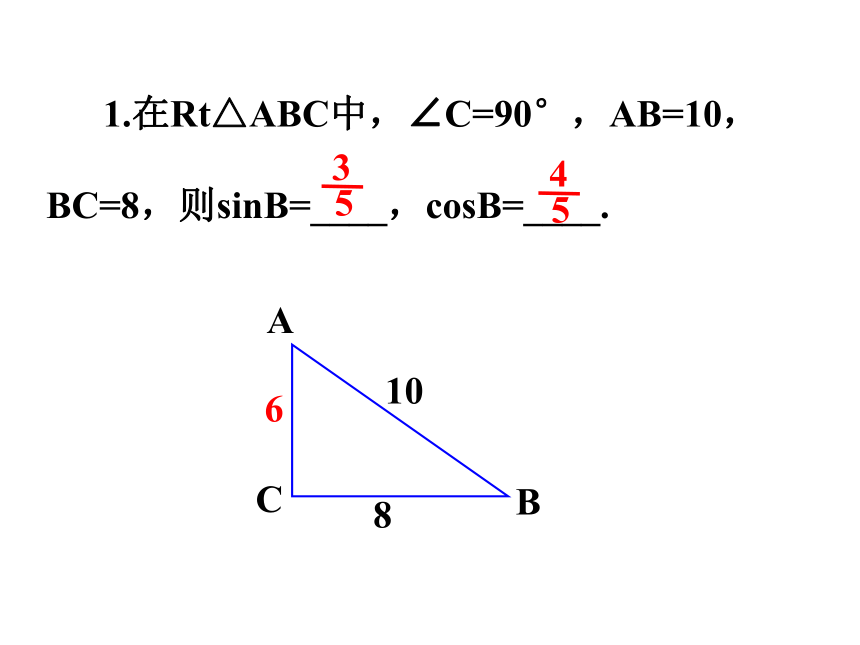


文档简介
(共23张PPT)
沪科版 九年级上册
23.1 锐角三角函数 (3)
教学目标:
1.运用三角函数的概念,自主探究求出三个特殊角的三角函数值.
2.熟记三个特殊角的三角函数值,并能准确地加以运用,即给出特殊角能说出它的三角函数值,反过来,给出特殊角的三角函数值,能说出相应的锐角的度数.
教学重点:三个特殊角的三角函数值及其运用.
教学难点:特殊角三角函数值的应用.
B
a
C
b
A
c
┏
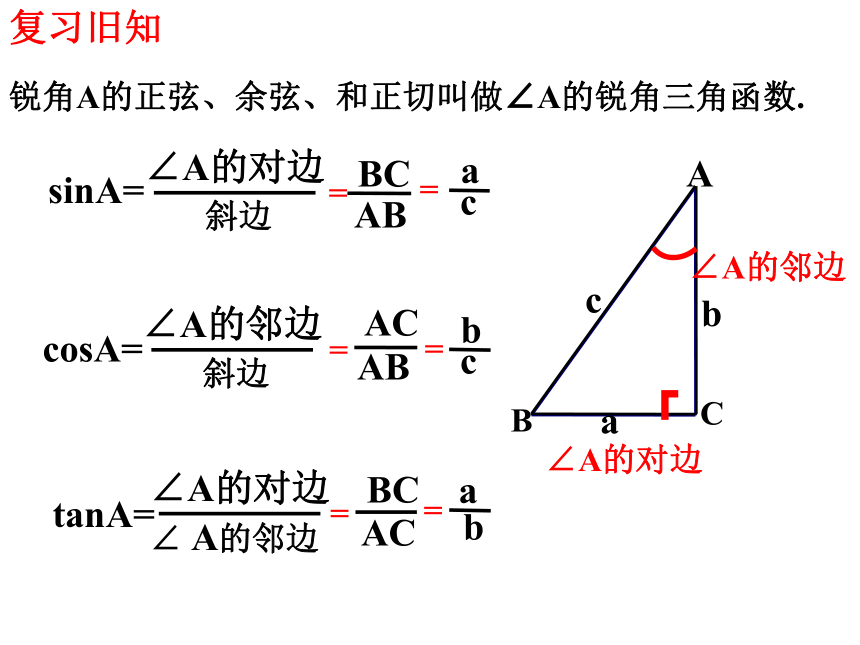
∠A的对边
斜边
∠A的对边
=
a
c
=
=
sinA=
BC
AB
=
cosA=
斜边
∠A的邻边
AC
AB
=
b
c
tanA=
∠ A的邻边
∠A的对边
BC
AC
=
a
b
∠A的邻边
锐角A的正弦、余弦、和正切叫做∠A的锐角三角函数.
复习旧知
1.在Rt△ABC中,∠C=90°,AB=10, BC=8,则sinB=____,cosB=____.
A
B
C
10
8
6
5
3
5
4
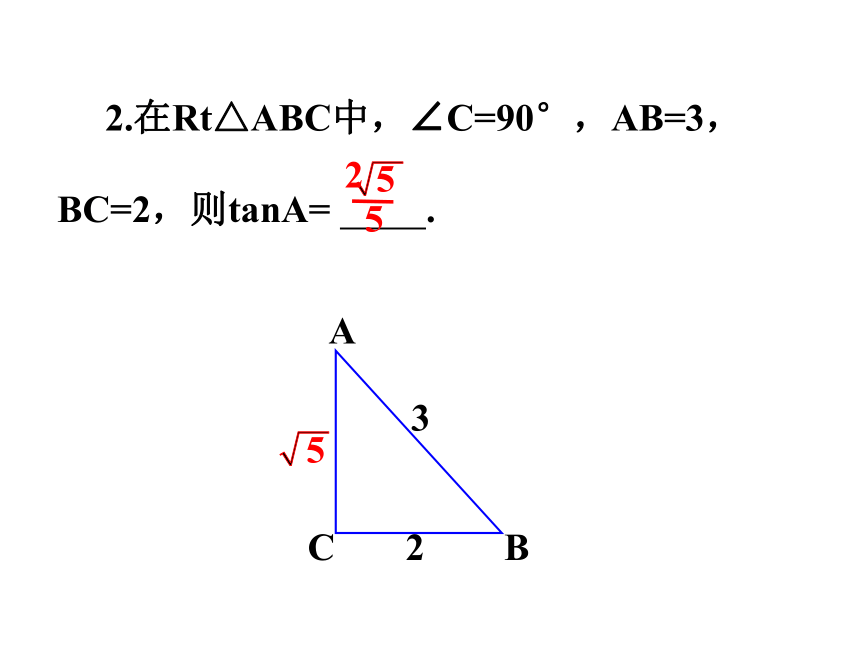
2.在Rt△ABC中,∠C=90°,AB=3,BC=2,则tanA= .
A
B
C
3
2
5
5
5
2
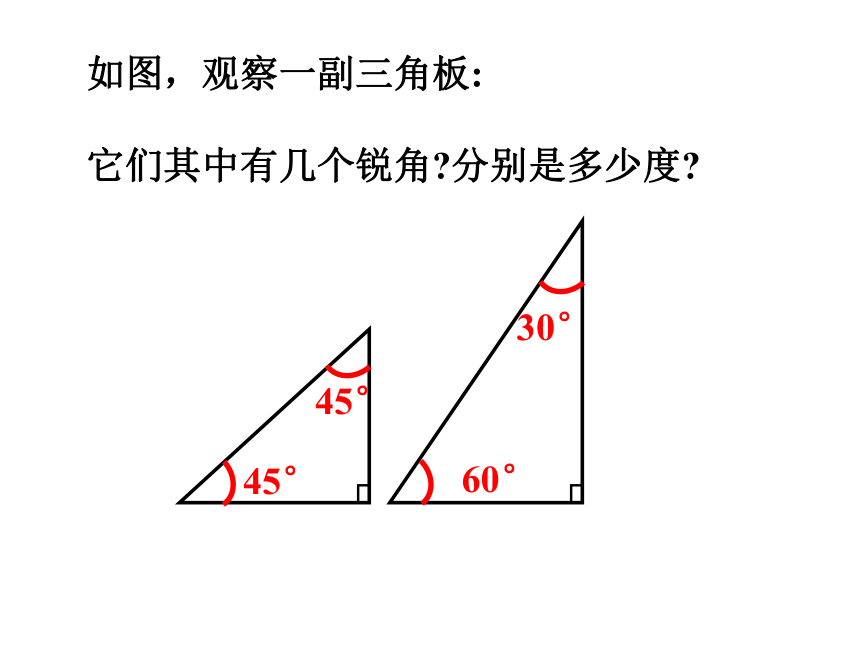
如图,观察一副三角板:
它们其中有几个锐角 分别是多少度
┌
┌
30°
60°
45°
45°
(1)sin30°=
(2)cos30°=
(3)tan30°=
30°角的各类三角函数值的探索
┌
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
1
2
3
1
2
2
3
1
3
3
3
=
30°
(1)sin45°=
(2)cos45°=
(3)tan45°=
45°角的各类三角函数值的探索
1
A
B
C
1
2
2
2
=
2
1
2
2
2
=
1
1
=1
45°
1
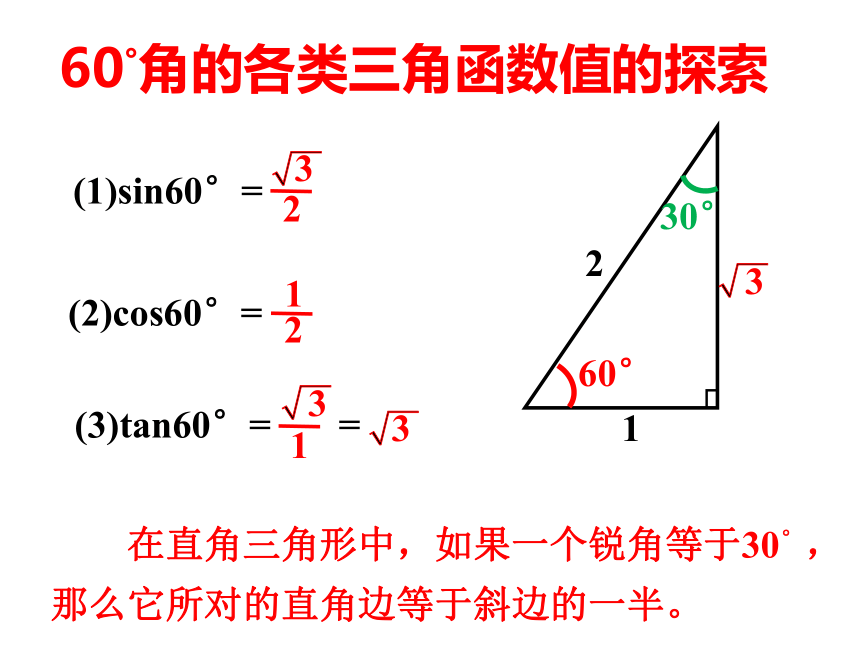
(1)sin60°=
(2)cos60°=
(3)tan60°=
60°角的各类三角函数值的探索
┌
60°
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
1
2
3
30°
2
3
1
2
1
3
3
=
三角函数 锐角α 正弦sinα 余弦cosα 正切tanα
30°
45°
60°
1
2
2
3
3
3
2
2
2
2
1
2
3
1
2
3
三个特殊锐角三角函数数值表
例4: 求下列各式的值:
(1)2sin60°+ 3tan30°+ tan45°;
(2) cos245° + tan60°cos30°.
解:(1)原式=
(2)原式=
1
2
+
2
3
=
+1
3
cos245°= (cos45°)2
( )2
2
2
+
=
2
4
+
3
2
2×
3×
3
3
+
3
+1
=
2
3
+1
3
×
2
3
=
+
3
2
=
2
练习: 计算:
(1) sin245° + cos245°
(2) 2sin30°+ 2cos60°+4 tan45°;
解:(1)原式=
(2)原式=
( )2
2
2
+
=
2
4
+
2
4
=1
( )2
2
2
2×
1
2
+
2×
1
2
+
4×1
=
1+1
+4
=6
练习: 计算:
(3) cos230° + sin245°-tan60°·tan30°.
解:(3)原式=
( )2
2
3
+
=
3
4
+
2
4
=
( )2
2
2
-
3
3
3
×
-1
1
4
2sin30°
2cos30°-1
练习: 计算:
(4)
sin60° -tan45°
tan60°-2tan45°
(5)
解:(4)原式=
2×
-1
1
2
2×
2
3
=
3
1
=
-1
2
3
+1
(5)原式=
-1
-2×1
2
3
3
=
3
-2
2
3
-2
=
1
2
1.如图所示,将30°的三角板的直角顶点放置在直线AB的O占处,使斜边CD∥AB,则α的余弦值为( ).
A. B. C. D.
1
2
3
4
2
2
3
2
A
C
D
O
B
α
巩固提高
D
∽
2.在△ABC中,若∣sinA- ∣+(cosB- )2=0,
则∠C的度数是( ).
A.30° B. 45° C. 75° D. 105°
3
2
2
2
C
3.计算:
2
2
sin45°+ sin60°
-2cos45°.
3
2
解:原式=
2
2
×
2
2
+
3
×
3
2
-
×
2
2
1
2
+
3
2
-
2
=
=
2
-
2
4.求下列各式的值:
(1)tan230°+2sin60°+tan45°sin30° - tan60°+cos230°
(2)
解:(1)原式=
cos60°
tan45° - sin45°
√
cos245° - 2cos45° +1
(3)
3
3
( )2
+
2
3
2×
+
1×
1
2
-
3
+
( )2
2
3
=
1
3
+
3
+
1
2
-
3
+
3
4
=
19
12
4.求下列各式的值:
(1)tan230°+2sin60°+tan45°sin30° - tan60°+cos230°
(2)
cos60°
tan45° - sin45°
√
cos245° - 2cos45° +1
(3)
解:(2)原式=
1 -
2
2
1
2
=
2 -
2
1
=
4 -2
2 +
2
=
2
2 +
2
4.求下列各式的值:
(1)tan230°+2sin60°+tan45°sin30° - tan60°+cos230°
(2)
cos60°
tan45° - sin45°
√
cos245° - 2cos45° +1
(3)
解:(3)原式=
√
(cos45° - 1)2
=
cos45° - 1
=
=
1 -
2
2
2
2
-1
| |
| |
今天作业
课本P122页第1 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
23.1 锐角三角函数 (3)
教学目标:
1.运用三角函数的概念,自主探究求出三个特殊角的三角函数值.
2.熟记三个特殊角的三角函数值,并能准确地加以运用,即给出特殊角能说出它的三角函数值,反过来,给出特殊角的三角函数值,能说出相应的锐角的度数.
教学重点:三个特殊角的三角函数值及其运用.
教学难点:特殊角三角函数值的应用.
B
a
C
b
A
c
┏
∠A的对边
斜边
∠A的对边
=
a
c
=
=
sinA=
BC
AB
=
cosA=
斜边
∠A的邻边
AC
AB
=
b
c
tanA=
∠ A的邻边
∠A的对边
BC
AC
=
a
b
∠A的邻边
锐角A的正弦、余弦、和正切叫做∠A的锐角三角函数.
复习旧知
1.在Rt△ABC中,∠C=90°,AB=10, BC=8,则sinB=____,cosB=____.
A
B
C
10
8
6
5
3
5
4
2.在Rt△ABC中,∠C=90°,AB=3,BC=2,则tanA= .
A
B
C
3
2
5
5
5
2
如图,观察一副三角板:
它们其中有几个锐角 分别是多少度
┌
┌
30°
60°
45°
45°
(1)sin30°=
(2)cos30°=
(3)tan30°=
30°角的各类三角函数值的探索
┌
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
1
2
3
1
2
2
3
1
3
3
3
=
30°
(1)sin45°=
(2)cos45°=
(3)tan45°=
45°角的各类三角函数值的探索
1
A
B
C
1
2
2
2
=
2
1
2
2
2
=
1
1
=1
45°
1
(1)sin60°=
(2)cos60°=
(3)tan60°=
60°角的各类三角函数值的探索
┌
60°
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
1
2
3
30°
2
3
1
2
1
3
3
=
三角函数 锐角α 正弦sinα 余弦cosα 正切tanα
30°
45°
60°
1
2
2
3
3
3
2
2
2
2
1
2
3
1
2
3
三个特殊锐角三角函数数值表
例4: 求下列各式的值:
(1)2sin60°+ 3tan30°+ tan45°;
(2) cos245° + tan60°cos30°.
解:(1)原式=
(2)原式=
1
2
+
2
3
=
+1
3
cos245°= (cos45°)2
( )2
2
2
+
=
2
4
+
3
2
2×
3×
3
3
+
3
+1
=
2
3
+1
3
×
2
3
=
+
3
2
=
2
练习: 计算:
(1) sin245° + cos245°
(2) 2sin30°+ 2cos60°+4 tan45°;
解:(1)原式=
(2)原式=
( )2
2
2
+
=
2
4
+
2
4
=1
( )2
2
2
2×
1
2
+
2×
1
2
+
4×1
=
1+1
+4
=6
练习: 计算:
(3) cos230° + sin245°-tan60°·tan30°.
解:(3)原式=
( )2
2
3
+
=
3
4
+
2
4
=
( )2
2
2
-
3
3
3
×
-1
1
4
2sin30°
2cos30°-1
练习: 计算:
(4)
sin60° -tan45°
tan60°-2tan45°
(5)
解:(4)原式=
2×
-1
1
2
2×
2
3
=
3
1
=
-1
2
3
+1
(5)原式=
-1
-2×1
2
3
3
=
3
-2
2
3
-2
=
1
2
1.如图所示,将30°的三角板的直角顶点放置在直线AB的O占处,使斜边CD∥AB,则α的余弦值为( ).
A. B. C. D.
1
2
3
4
2
2
3
2
A
C
D
O
B
α
巩固提高
D
∽
2.在△ABC中,若∣sinA- ∣+(cosB- )2=0,
则∠C的度数是( ).
A.30° B. 45° C. 75° D. 105°
3
2
2
2
C
3.计算:
2
2
sin45°+ sin60°
-2cos45°.
3
2
解:原式=
2
2
×
2
2
+
3
×
3
2
-
×
2
2
1
2
+
3
2
-
2
=
=
2
-
2
4.求下列各式的值:
(1)tan230°+2sin60°+tan45°sin30° - tan60°+cos230°
(2)
解:(1)原式=
cos60°
tan45° - sin45°
√
cos245° - 2cos45° +1
(3)
3
3
( )2
+
2
3
2×
+
1×
1
2
-
3
+
( )2
2
3
=
1
3
+
3
+
1
2
-
3
+
3
4
=
19
12
4.求下列各式的值:
(1)tan230°+2sin60°+tan45°sin30° - tan60°+cos230°
(2)
cos60°
tan45° - sin45°
√
cos245° - 2cos45° +1
(3)
解:(2)原式=
1 -
2
2
1
2
=
2 -
2
1
=
4 -2
2 +
2
=
2
2 +
2
4.求下列各式的值:
(1)tan230°+2sin60°+tan45°sin30° - tan60°+cos230°
(2)
cos60°
tan45° - sin45°
√
cos245° - 2cos45° +1
(3)
解:(3)原式=
√
(cos45° - 1)2
=
cos45° - 1
=
=
1 -
2
2
2
2
-1
| |
| |
今天作业
课本P122页第1 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
