23.1 锐角三角函数 (1) 课件(28张PPT)
文档属性
| 名称 | 23.1 锐角三角函数 (1) 课件(28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 00:00:00 | ||
图片预览



文档简介
(共28张PPT)
沪科版 九年级上册
23.1 锐角三角函数 (1)
教学目标
1.联系生活实际,经历探索直角三角形中边角关系的过程,了解当锐角固定时,它的对边,邻边中两边比值也是固定不变的,这一事实,初步理解角度与数值(比值)之间的一一对应关系.
2.了解直角三角形中锐角三角函数的概念能正确运用tanA表示直角三角形(锐角)中对边与邻边的比.
3.根据三角形边角关系,能够由给出的边长求tanA.
教学重点:正切函数的概念.
教学难点:正切函数的概念.
这是南宁市青山英华路口一段长约300米的大坡 .
因坡长且陡、路窄车多等因素,导致该路段时常被“卡喉”.
引入课题
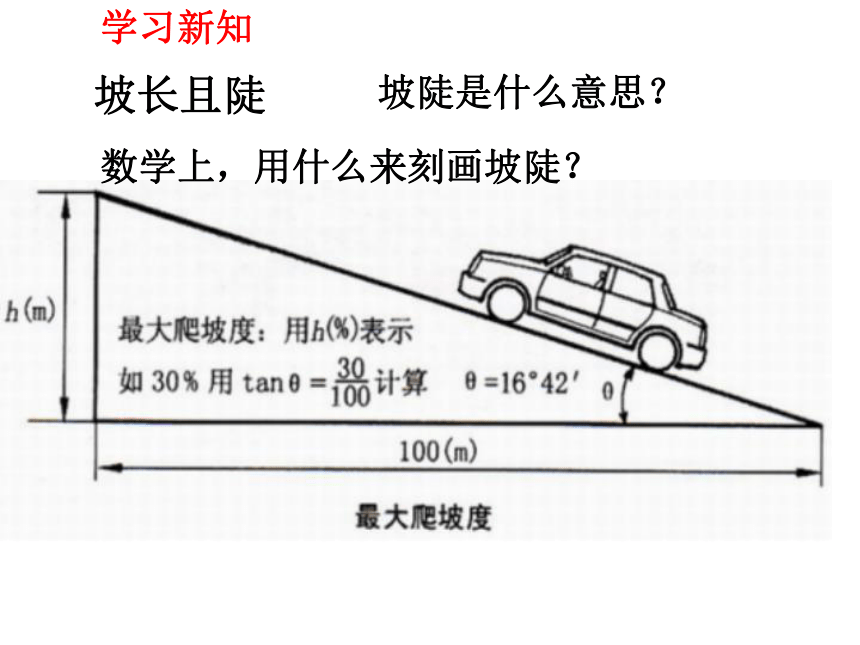
坡长且陡
坡陡是什么意思?
数学上,用什么来刻画坡陡?
学习新知
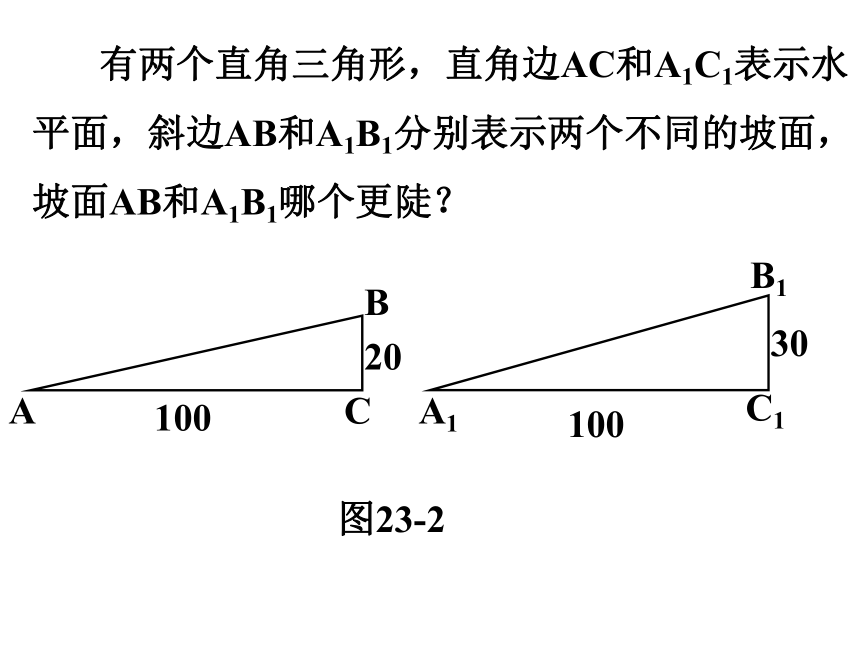
图23-2
100
C1
30
A1
B1
100
C
B
A
20
有两个直角三角形,直角边AC和A1C1表示水平面,斜边AB和A1B1分别表示两个不同的坡面,坡面AB和A1B1哪个更陡?
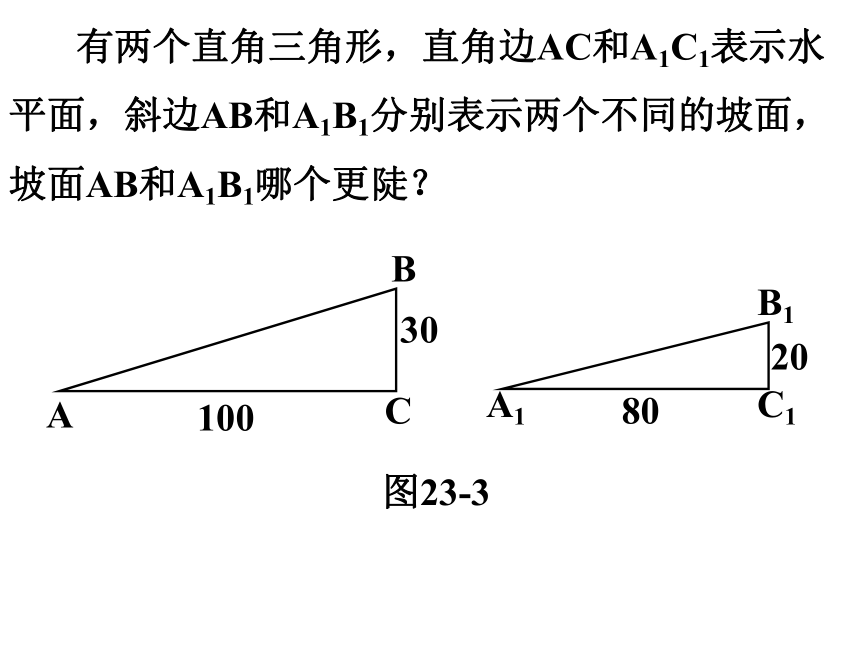
图23-3
80
C1
20
A1
100
C
B
A
30
有两个直角三角形,直角边AC和A1C1表示水平面,斜边AB和A1B1分别表示两个不同的坡面,坡面AB和A1B1哪个更陡?
B1
A
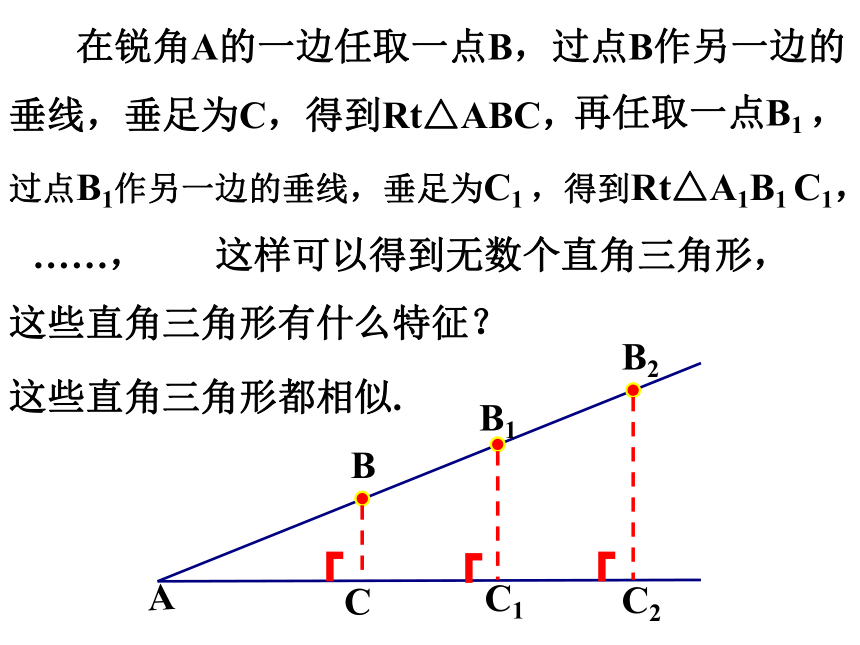
在锐角A的一边任取一点B,过点B作另一边的垂线,垂足为C,得到Rt△ABC,
B1
B2
C1
C2
┏
┏
再任取一点B1 ,
过点B1作另一边的垂线,垂足为C1 ,得到Rt△A1B1 C1,
……,
这样可以得到无数个直角三角形,
这些直角三角形有什么特征?
这些直角三角形都相似.
B
C
┏
B
C
A
┏
B1
B2
C1
C2
┏
┏
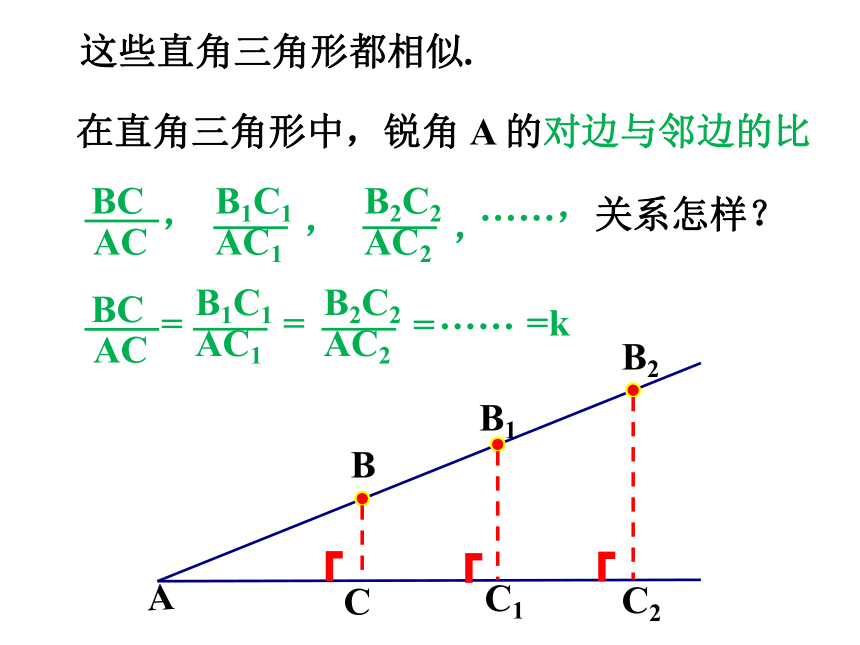
这些直角三角形都相似.
在直角三角形中,锐角 A 的对边与邻边的比
AC
BC
,
AC1
B1C1
,
AC2
B2C2
,
……,
关系怎样?
AC
BC
=
AC1
B1C1
=
AC2
B2C2
=
……
=k
B
C
A
┏
B1
B2
C1
C2
┏
┏
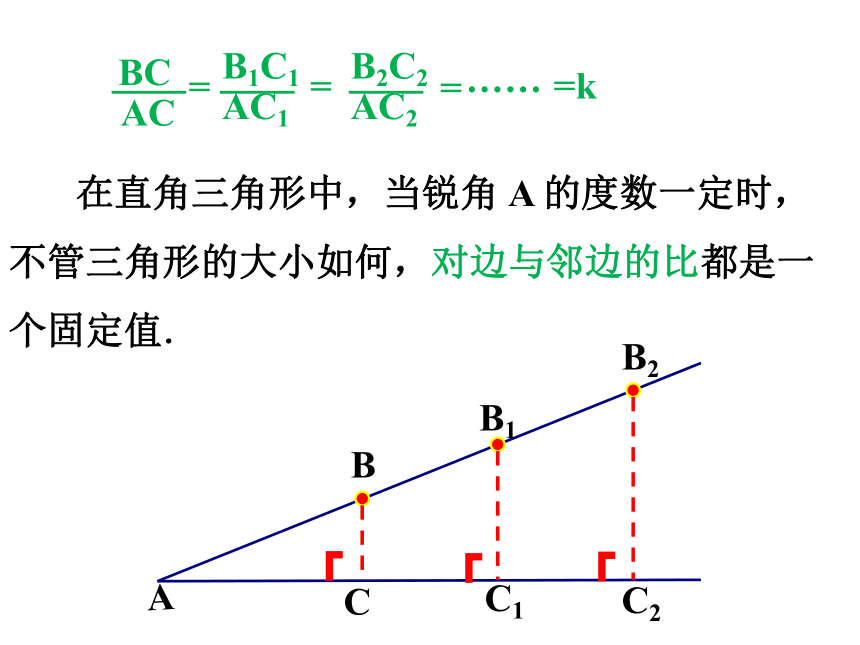
在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,对边与邻边的比都是一个固定值.
AC
BC
=
AC1
B1C1
=
AC2
B2C2
=
……
=k
在直角三角形中,当锐角A取一定度数时,
∠A的对边与邻边的比是一个固定值,
叫做∠A的正切.
B
C
A
┏
=
tanA=
∠A的邻边
∠A的对边
BC
AC
=
a
b
=
tanB=
∠B的邻边
∠B的对边
BC
AC
=
b
a
a
b
记作tanA.
例1 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,求tanA和tanB.
A
B
C
3
4
解:在Rt△ABC中,∵∠C=90°,
tanB=
AC
BC
=
4
3
tanA=
BC
AC
=
3
4
例题解析
∴
1.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则tanB的值是( ).
A. B. C. D.
练习巩固
A
B
C
6
5
D
4
5
3
5
3
4
4
3
C
2.在Rt△ABC中,若CA=CB,AB=9 ,点D在BC上,连接AC若tan∠CAD= ,则BD的长为 .
1
3
A
B
C
D
6
3.在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若AC= ,BC=2. 求tan∠ACD的值.
A
B
C
2
D
解:在Rt△ABC中,∵∠ACB=90°,
∴ ∠A+∠B=90°.
∵CD⊥AB,
∴∠CDA=90°.
∴ ∠A+∠ACD=90°,
∴∠ACD=∠B.
在Rt△ABC中,
tanB=
AC
BC
=
2
∴tan∠ACD=
tanB
=
2
l
h
α
i=h:l
正切经常用来描述坡面的坡度.
坡面的铅直高度h和水平长度l 的比叫做坡面的坡度.
i=
h
l
(坡度通常写成h:l 的形式)
记作i .
学习新知
l
h
α
i=h:l
正切经常用来描述坡面的坡度.
坡面与水平面的夹角叫做坡角(或称倾斜角),
i=
h
l
=tanα
坡度越大,坡角越大,坡面就越陡.
于是有:
记作α .
图23-3
100
C
B
A
30
有两个直角三角形,直角边AC和A1C1表示水平面,斜边AB和A1B1分别表示两个不同的坡面,坡面AB和A1B1哪个更陡?
80
C1
20
A1
B1
练习巩固
1.在Rt△ABC中,当∠A角度固定,对边与邻边比值不变
2.正切概念:在Rt△ABC中,把锐角A的对边与邻边之比叫做正切,记作:tanA=
。
3. 坡度、坡比: i=
4. 坡角α.
课堂小结
i=tanα
∠A的邻边
∠A的对边
h
l
数学花絮
生活中的坡度
数学花絮
生活中的坡度
盘山公路减小了道路坡度、使车辆能够爬坡
数学花絮
生活中的坡度
数学花絮
生活中的坡度
今天作业
课本P114页第2,3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
23.1 锐角三角函数 (1)
教学目标
1.联系生活实际,经历探索直角三角形中边角关系的过程,了解当锐角固定时,它的对边,邻边中两边比值也是固定不变的,这一事实,初步理解角度与数值(比值)之间的一一对应关系.
2.了解直角三角形中锐角三角函数的概念能正确运用tanA表示直角三角形(锐角)中对边与邻边的比.
3.根据三角形边角关系,能够由给出的边长求tanA.
教学重点:正切函数的概念.
教学难点:正切函数的概念.
这是南宁市青山英华路口一段长约300米的大坡 .
因坡长且陡、路窄车多等因素,导致该路段时常被“卡喉”.
引入课题
坡长且陡
坡陡是什么意思?
数学上,用什么来刻画坡陡?
学习新知
图23-2
100
C1
30
A1
B1
100
C
B
A
20
有两个直角三角形,直角边AC和A1C1表示水平面,斜边AB和A1B1分别表示两个不同的坡面,坡面AB和A1B1哪个更陡?
图23-3
80
C1
20
A1
100
C
B
A
30
有两个直角三角形,直角边AC和A1C1表示水平面,斜边AB和A1B1分别表示两个不同的坡面,坡面AB和A1B1哪个更陡?
B1
A
在锐角A的一边任取一点B,过点B作另一边的垂线,垂足为C,得到Rt△ABC,
B1
B2
C1
C2
┏
┏
再任取一点B1 ,
过点B1作另一边的垂线,垂足为C1 ,得到Rt△A1B1 C1,
……,
这样可以得到无数个直角三角形,
这些直角三角形有什么特征?
这些直角三角形都相似.
B
C
┏
B
C
A
┏
B1
B2
C1
C2
┏
┏
这些直角三角形都相似.
在直角三角形中,锐角 A 的对边与邻边的比
AC
BC
,
AC1
B1C1
,
AC2
B2C2
,
……,
关系怎样?
AC
BC
=
AC1
B1C1
=
AC2
B2C2
=
……
=k
B
C
A
┏
B1
B2
C1
C2
┏
┏
在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,对边与邻边的比都是一个固定值.
AC
BC
=
AC1
B1C1
=
AC2
B2C2
=
……
=k
在直角三角形中,当锐角A取一定度数时,
∠A的对边与邻边的比是一个固定值,
叫做∠A的正切.
B
C
A
┏
=
tanA=
∠A的邻边
∠A的对边
BC
AC
=
a
b
=
tanB=
∠B的邻边
∠B的对边
BC
AC
=
b
a
a
b
记作tanA.
例1 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,求tanA和tanB.
A
B
C
3
4
解:在Rt△ABC中,∵∠C=90°,
tanB=
AC
BC
=
4
3
tanA=
BC
AC
=
3
4
例题解析
∴
1.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则tanB的值是( ).
A. B. C. D.
练习巩固
A
B
C
6
5
D
4
5
3
5
3
4
4
3
C
2.在Rt△ABC中,若CA=CB,AB=9 ,点D在BC上,连接AC若tan∠CAD= ,则BD的长为 .
1
3
A
B
C
D
6
3.在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若AC= ,BC=2. 求tan∠ACD的值.
A
B
C
2
D
解:在Rt△ABC中,∵∠ACB=90°,
∴ ∠A+∠B=90°.
∵CD⊥AB,
∴∠CDA=90°.
∴ ∠A+∠ACD=90°,
∴∠ACD=∠B.
在Rt△ABC中,
tanB=
AC
BC
=
2
∴tan∠ACD=
tanB
=
2
l
h
α
i=h:l
正切经常用来描述坡面的坡度.
坡面的铅直高度h和水平长度l 的比叫做坡面的坡度.
i=
h
l
(坡度通常写成h:l 的形式)
记作i .
学习新知
l
h
α
i=h:l
正切经常用来描述坡面的坡度.
坡面与水平面的夹角叫做坡角(或称倾斜角),
i=
h
l
=tanα
坡度越大,坡角越大,坡面就越陡.
于是有:
记作α .
图23-3
100
C
B
A
30
有两个直角三角形,直角边AC和A1C1表示水平面,斜边AB和A1B1分别表示两个不同的坡面,坡面AB和A1B1哪个更陡?
80
C1
20
A1
B1
练习巩固
1.在Rt△ABC中,当∠A角度固定,对边与邻边比值不变
2.正切概念:在Rt△ABC中,把锐角A的对边与邻边之比叫做正切,记作:tanA=
。
3. 坡度、坡比: i=
4. 坡角α.
课堂小结
i=tanα
∠A的邻边
∠A的对边
h
l
数学花絮
生活中的坡度
数学花絮
生活中的坡度
盘山公路减小了道路坡度、使车辆能够爬坡
数学花絮
生活中的坡度
数学花絮
生活中的坡度
今天作业
课本P114页第2,3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
