【新课标】3.5 探索与表达规律 课件(共31张PPT)
文档属性
| 名称 | 【新课标】3.5 探索与表达规律 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 16:58:40 | ||
图片预览





文档简介
(共31张PPT)
3.5 探索与表达规律
北师版七年级上册
教学目标
1.通过探索数量关系,理解探索规律的步骤,在探究知识的过程中培养创新能力,培养良好的思维品质。
2.会用代数式表示简单问题中的数量关系,能用合并同类项、去括号等法则验证所探索的规律。
3.通过动手、动脑以及利用转化、类比的方法去探索,培养观察能力、交往协作能力、动手能力、归纳概括能力、创新能力、应用意识。
教学重难点
重点:
会用代数式表示简单问题中的数量关系,能用合并同类项、去括号等法则验证所探索的规律。
难点:
培养观察力、交往协作能力、动手能力、归纳概括能力、创新能力、应用意识。
新知导入
请大家默选一个你喜欢的两位数,经过提供的运算程序,告诉我你的结果,我能猜出你的喜好!你相信吗?
十位数字
+个位数字
结果
乘以2
?
+3
?
×5
?
新知讲解
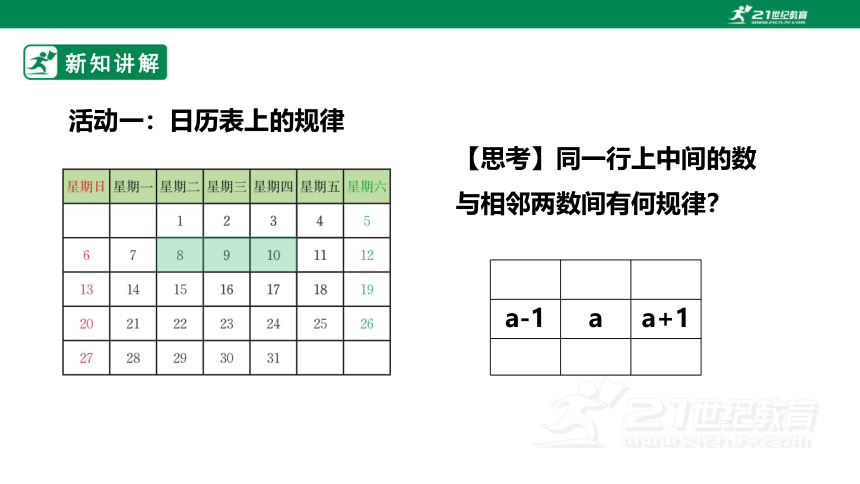
活动一:日历表上的规律
【思考】同一行上中间的数与相邻两数间有何规律?
a-1 a a+1
新知讲解
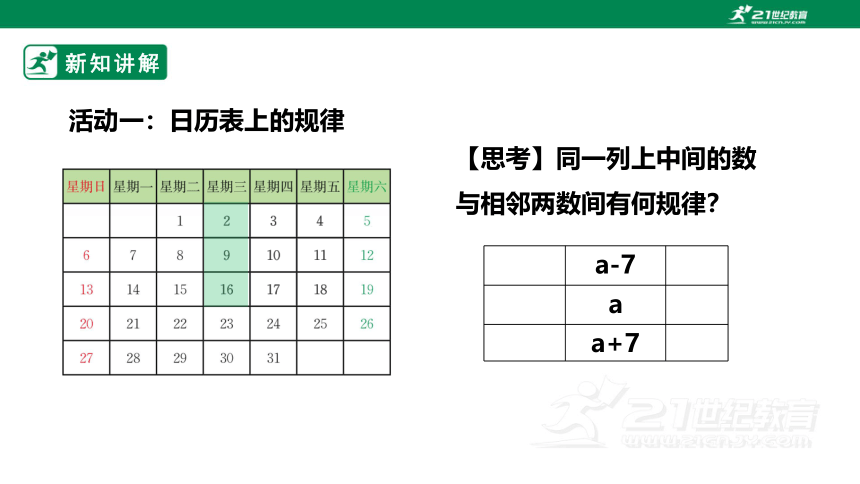
活动一:日历表上的规律
【思考】同一列上中间的数与相邻两数间有何规律?
a-7
a
a+7
新知讲解
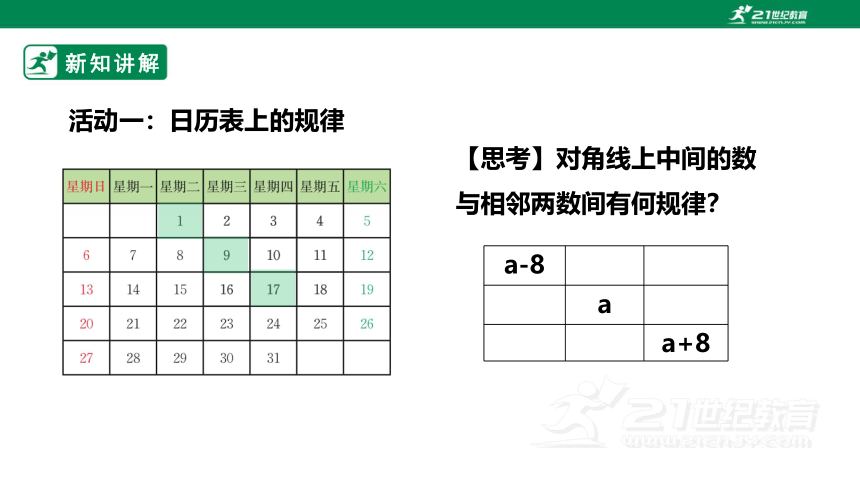
活动一:日历表上的规律
【思考】对角线上中间的数与相邻两数间有何规律?
a-8
a
a+8
新知讲解
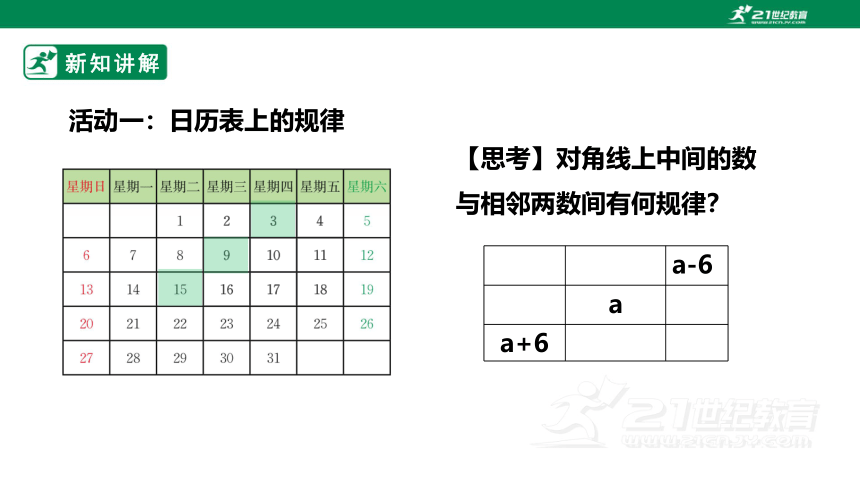
活动一:日历表上的规律
【思考】对角线上中间的数与相邻两数间有何规律?
a-6
a
a+6
新知讲解
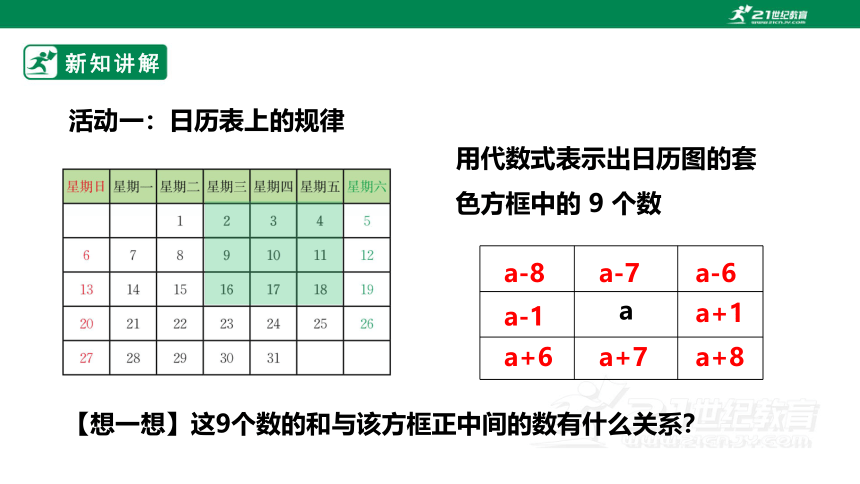
活动一:日历表上的规律
用代数式表示出日历图的套色方框中的 9 个数
a
a-1
a+1
a-7
a+7
a-8
a+6
a+8
a-6
【想一想】这9个数的和与该方框正中间的数有什么关系?
新知讲解
活动一:日历表上的规律
2+3+4+9+10+11+16+17+18
=90=10×9
用代数式表示:
a-8+a-7+a-6+a-1+a+a+1
+a+6+a+7+a+8
=9a
新知讲解
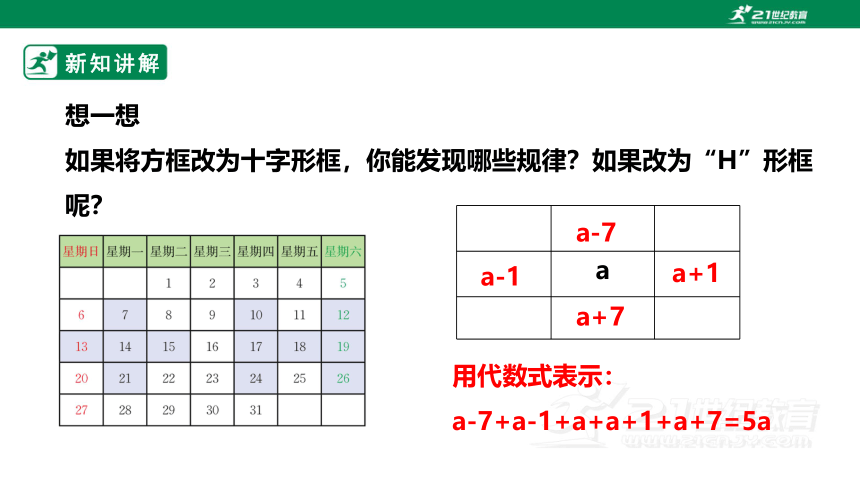
想一想
如果将方框改为十字形框,你能发现哪些规律?如果改为“H”形框呢?
a
a-1
a+1
a-7
a+7
用代数式表示:
a-7+a-1+a+a+1+a+7=5a
新知讲解
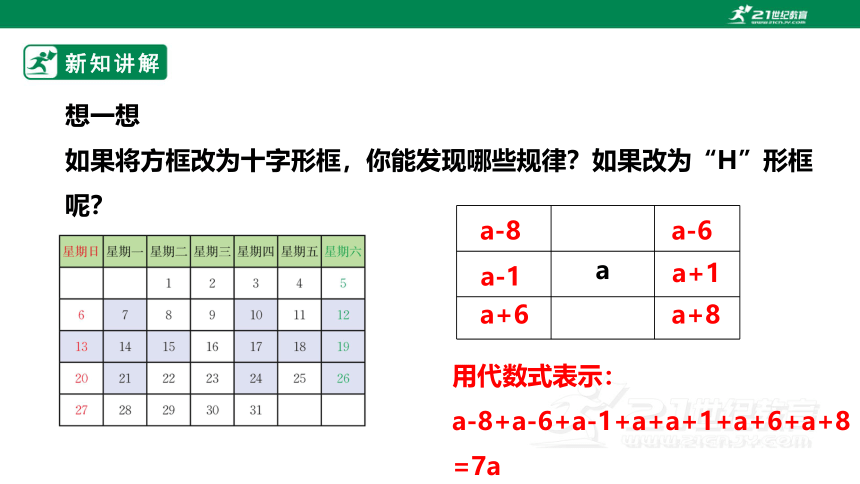
想一想
如果将方框改为十字形框,你能发现哪些规律?如果改为“H”形框呢?
a
a-1
a+1
用代数式表示:
a-8+a-6+a-1+a+a+1+a+6+a+8
=7a
a-8
a+6
a+8
a-6
新知讲解
对于有关数与算式的规律问题,首先要认真观察,从给出的有限的几个入手观察数与数之间的规律及算式本身存在的规律,把等式横向、纵向分别进行比较,找出其中的不变部分与变化部分、数与式子的序号之间的关系,然后找出其中的变化规律.
【总结归纳】
新知讲解
【做一做】下面是用棋子摆成的“小屋子”.摆第 10 个这样的“小屋子”需要多少枚棋子?摆第 n 个这样的“小屋子”呢?你是如何得到的?
新知讲解
第1个“小房子”共有(1+4)枚棋子,
第2个“小房子”共有(1+2+8)枚棋子,
第3个“小房子”共有(1+2×2+12)枚棋子,
第10个“小房子”共有(1+2×9+4×10)枚棋子,即59枚棋子,
第n个“小房子”共有[1+2×(n-1)+4n]枚棋子,即(6n-1)枚棋子,
新知讲解
图形中的规律探究方法通常为将图形转化为一列数,由这一列数寻找规律,或观察图形结构特点,归纳相对于某个基础图形的递推规律,从而将图形转化为一列数或等式,继而探究规律.
【总结归纳】
新知讲解
活动二:猜数游戏
游戏规则:你在心里想好一个两位数,将十位数字乘2,然后加上3,再乘5,然后再加上个位数字.
把你的结果告诉我,我就知道你心里想的两位数.
新知讲解
【想一想】
如果原来的两位数是12,则最后得到的两位数是多少?
如果最后得到的两位数是93 ,你能求出原来的两位数吗?
27
78
填表:
38
54
序号 原数 新数
1 23
2 36
3 69
…
21
新知讲解
小组讨论:每个同学都准备一个数试一试,你能说出其中的规律吗?
设这个两位数的十位数字是a,个位数字是b .
得到的新数是 :5(2a+3) + b.
课堂练习
1.将从1开始的连续自然数按以下规律排列:
则2 022在第________行.
45
课堂练习
2.观察如图所示的“蜂窝图”.
则第n个图案中的“ ”的个数是__________(用含有n的代数式表示).
3n+1
课堂练习
3.下列图形都是由同样大小的黑色正方形纸片组成的,其中第①个图中有3张黑色正方形纸片,第②个图中有5张黑色正方形纸片,第③个图中有7张黑色正方形纸片,…,按此规律排列下去,第⑥个图中黑色正方形纸片的张数为( )
A.11 B.13 C.15 D.17
B
课堂练习
4.将一些相同的“○”按如图所示摆放,观察每个图形中“○ ”的个数,若第n个图形中的“○”的个数是78,则n的值是( )
A.11 B.12 C.13 D.14
B
课堂练习
5.用正三角形、正方形和正六边形按如图所示的规律拼图案,即从第2个图案开始,每个图案中正三角形的个数都比上一个图案中正三角形的个数多4,则第n个图案中正三角形的个数为( )
A.2n-1 B.3n-2 C.4n+2 D.4n-2
C
课堂练习
6.我们知道简便计算的好处,事实上,简便计算在好多地方都存在,观察下列等式:
152=1×2×100+25=225,
252=2×3×100+25=625,
352=3×4×100+25=1 225,….
(1)根据上述等式反映出的规律填空:
952=_________________=___________.
9×10×100+25
9 025
课堂练习
6.我们知道简便计算的好处,事实上,简便计算在好多地方都存在,观察下列等式:
152=1×2×100+25=225,
252=2×3×100+25=625,
352=3×4×100+25=1 225,….
(2)设这类等式左边两位数的十位数字为a,请用一个含a的代数式表示其结果.
解:根据规律得出结论:
(10a+5)2=a·(a+1)×100+25=100a(a+1)+25.
课堂总结
本节课你学到了什么?
1. 探索规律的关键:注意观察已知的对应数值(图形)的变化规律,从中发现数量关系或图形的变化规律,即得到规律.
2. 探索规律的步骤:(1)从具体的题目出发,用列表或列举的方式,把各数量或图形的变化特点展现在图表当中;(2)认真观察图表或图形,通过合理联想,大胆猜想,总结归纳,得出数字或图形间的变化规律,形成结论;(3)验证结论的正误.
板书设计
课题:3.5 探索与表达规律
教师板演区
学生展示区
一、日历表上的规律
二、猜数游戏
三、探索规律的步骤.
作业布置
课本 P99 习题3.8
P100 习题3.9
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.5 探索与表达规律
北师版七年级上册
教学目标
1.通过探索数量关系,理解探索规律的步骤,在探究知识的过程中培养创新能力,培养良好的思维品质。
2.会用代数式表示简单问题中的数量关系,能用合并同类项、去括号等法则验证所探索的规律。
3.通过动手、动脑以及利用转化、类比的方法去探索,培养观察能力、交往协作能力、动手能力、归纳概括能力、创新能力、应用意识。
教学重难点
重点:
会用代数式表示简单问题中的数量关系,能用合并同类项、去括号等法则验证所探索的规律。
难点:
培养观察力、交往协作能力、动手能力、归纳概括能力、创新能力、应用意识。
新知导入
请大家默选一个你喜欢的两位数,经过提供的运算程序,告诉我你的结果,我能猜出你的喜好!你相信吗?
十位数字
+个位数字
结果
乘以2
?
+3
?
×5
?
新知讲解
活动一:日历表上的规律
【思考】同一行上中间的数与相邻两数间有何规律?
a-1 a a+1
新知讲解
活动一:日历表上的规律
【思考】同一列上中间的数与相邻两数间有何规律?
a-7
a
a+7
新知讲解
活动一:日历表上的规律
【思考】对角线上中间的数与相邻两数间有何规律?
a-8
a
a+8
新知讲解
活动一:日历表上的规律
【思考】对角线上中间的数与相邻两数间有何规律?
a-6
a
a+6
新知讲解
活动一:日历表上的规律
用代数式表示出日历图的套色方框中的 9 个数
a
a-1
a+1
a-7
a+7
a-8
a+6
a+8
a-6
【想一想】这9个数的和与该方框正中间的数有什么关系?
新知讲解
活动一:日历表上的规律
2+3+4+9+10+11+16+17+18
=90=10×9
用代数式表示:
a-8+a-7+a-6+a-1+a+a+1
+a+6+a+7+a+8
=9a
新知讲解
想一想
如果将方框改为十字形框,你能发现哪些规律?如果改为“H”形框呢?
a
a-1
a+1
a-7
a+7
用代数式表示:
a-7+a-1+a+a+1+a+7=5a
新知讲解
想一想
如果将方框改为十字形框,你能发现哪些规律?如果改为“H”形框呢?
a
a-1
a+1
用代数式表示:
a-8+a-6+a-1+a+a+1+a+6+a+8
=7a
a-8
a+6
a+8
a-6
新知讲解
对于有关数与算式的规律问题,首先要认真观察,从给出的有限的几个入手观察数与数之间的规律及算式本身存在的规律,把等式横向、纵向分别进行比较,找出其中的不变部分与变化部分、数与式子的序号之间的关系,然后找出其中的变化规律.
【总结归纳】
新知讲解
【做一做】下面是用棋子摆成的“小屋子”.摆第 10 个这样的“小屋子”需要多少枚棋子?摆第 n 个这样的“小屋子”呢?你是如何得到的?
新知讲解
第1个“小房子”共有(1+4)枚棋子,
第2个“小房子”共有(1+2+8)枚棋子,
第3个“小房子”共有(1+2×2+12)枚棋子,
第10个“小房子”共有(1+2×9+4×10)枚棋子,即59枚棋子,
第n个“小房子”共有[1+2×(n-1)+4n]枚棋子,即(6n-1)枚棋子,
新知讲解
图形中的规律探究方法通常为将图形转化为一列数,由这一列数寻找规律,或观察图形结构特点,归纳相对于某个基础图形的递推规律,从而将图形转化为一列数或等式,继而探究规律.
【总结归纳】
新知讲解
活动二:猜数游戏
游戏规则:你在心里想好一个两位数,将十位数字乘2,然后加上3,再乘5,然后再加上个位数字.
把你的结果告诉我,我就知道你心里想的两位数.
新知讲解
【想一想】
如果原来的两位数是12,则最后得到的两位数是多少?
如果最后得到的两位数是93 ,你能求出原来的两位数吗?
27
78
填表:
38
54
序号 原数 新数
1 23
2 36
3 69
…
21
新知讲解
小组讨论:每个同学都准备一个数试一试,你能说出其中的规律吗?
设这个两位数的十位数字是a,个位数字是b .
得到的新数是 :5(2a+3) + b.
课堂练习
1.将从1开始的连续自然数按以下规律排列:
则2 022在第________行.
45
课堂练习
2.观察如图所示的“蜂窝图”.
则第n个图案中的“ ”的个数是__________(用含有n的代数式表示).
3n+1
课堂练习
3.下列图形都是由同样大小的黑色正方形纸片组成的,其中第①个图中有3张黑色正方形纸片,第②个图中有5张黑色正方形纸片,第③个图中有7张黑色正方形纸片,…,按此规律排列下去,第⑥个图中黑色正方形纸片的张数为( )
A.11 B.13 C.15 D.17
B
课堂练习
4.将一些相同的“○”按如图所示摆放,观察每个图形中“○ ”的个数,若第n个图形中的“○”的个数是78,则n的值是( )
A.11 B.12 C.13 D.14
B
课堂练习
5.用正三角形、正方形和正六边形按如图所示的规律拼图案,即从第2个图案开始,每个图案中正三角形的个数都比上一个图案中正三角形的个数多4,则第n个图案中正三角形的个数为( )
A.2n-1 B.3n-2 C.4n+2 D.4n-2
C
课堂练习
6.我们知道简便计算的好处,事实上,简便计算在好多地方都存在,观察下列等式:
152=1×2×100+25=225,
252=2×3×100+25=625,
352=3×4×100+25=1 225,….
(1)根据上述等式反映出的规律填空:
952=_________________=___________.
9×10×100+25
9 025
课堂练习
6.我们知道简便计算的好处,事实上,简便计算在好多地方都存在,观察下列等式:
152=1×2×100+25=225,
252=2×3×100+25=625,
352=3×4×100+25=1 225,….
(2)设这类等式左边两位数的十位数字为a,请用一个含a的代数式表示其结果.
解:根据规律得出结论:
(10a+5)2=a·(a+1)×100+25=100a(a+1)+25.
课堂总结
本节课你学到了什么?
1. 探索规律的关键:注意观察已知的对应数值(图形)的变化规律,从中发现数量关系或图形的变化规律,即得到规律.
2. 探索规律的步骤:(1)从具体的题目出发,用列表或列举的方式,把各数量或图形的变化特点展现在图表当中;(2)认真观察图表或图形,通过合理联想,大胆猜想,总结归纳,得出数字或图形间的变化规律,形成结论;(3)验证结论的正误.
板书设计
课题:3.5 探索与表达规律
教师板演区
学生展示区
一、日历表上的规律
二、猜数游戏
三、探索规律的步骤.
作业布置
课本 P99 习题3.8
P100 习题3.9
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
