18.1.1勾股定理[下学期]
文档属性
| 名称 | 18.1.1勾股定理[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-10 13:58:00 | ||
图片预览





文档简介
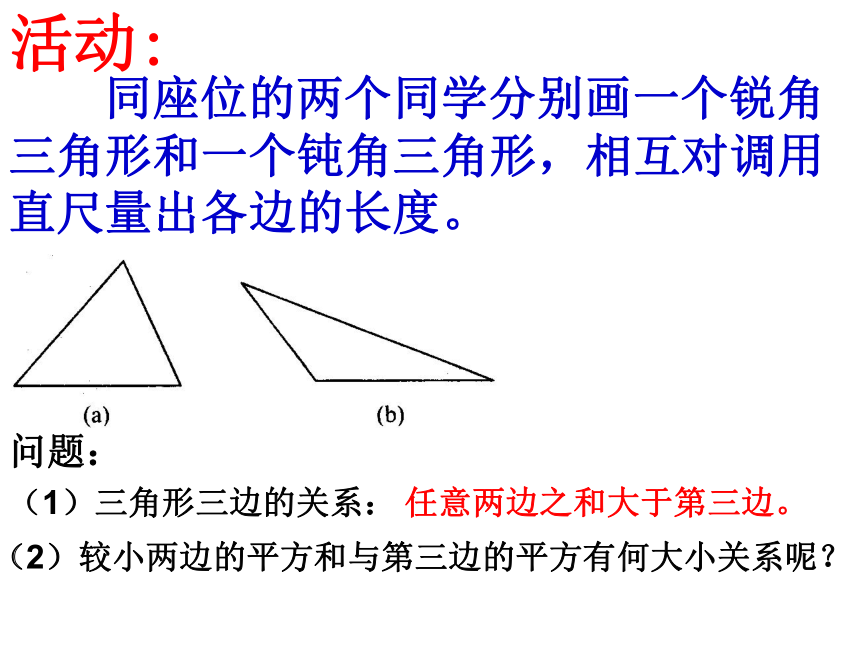
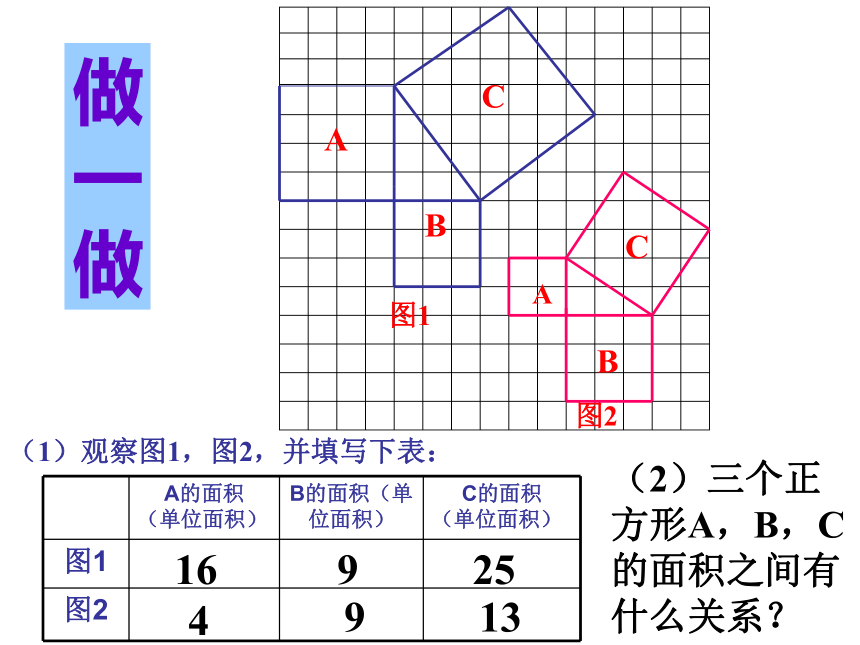
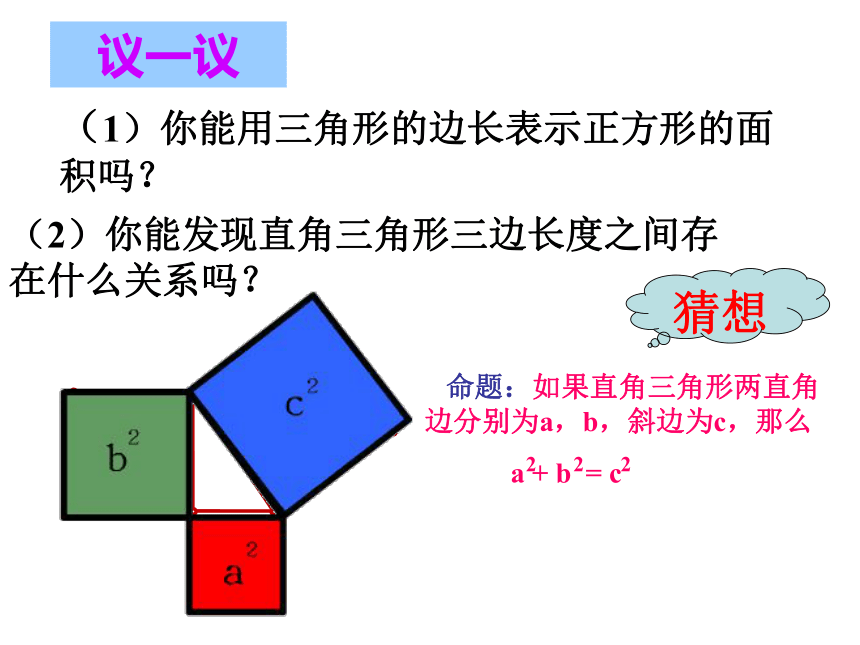
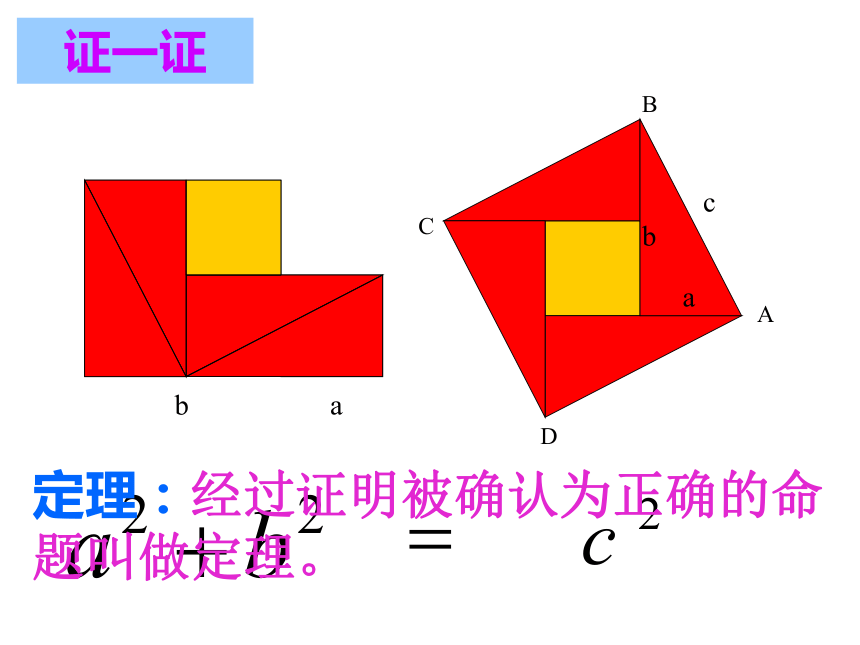
课件25张PPT。18.1.1勾股定理玉环县实验学校 黄成满活动: 同座位的两个同学分别画一个锐角三角形和一个钝角三角形,相互对调用直尺量出各边的长度。(2)较小两边的平方和与第三边的平方有何大小关系呢?问题:(1)三角形三边的关系:任意两边之和大于第三边。讲故事同学们,我们也来观察图中的地面,看看你能发现什么?是否和大哲学家有同样的发现呢?你能发现图中的等腰直角三角形有什么性质吗?做一做(1)观察图1,图2,并填写下表:(2)三个正方形A,B,C的面积之间有什么关系?169254913议一议(1)你能用三角形的边长表示正方形的面积吗?猜想(2)你能发现直角三角形三边长度之间存在什么关系吗?证一证定理:经过证明被确认为正确的命题叫做定理。2002年,在北京举行的国际数学家大会会标在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.在西方又称毕达哥拉斯定理!a2 + b2c2 - b2c2 - a2=c2 =a2=b2 勾股定理(gou-gu theorem)美国总统的证明加菲尔德 (James A. Garfield; 1831 ? 1881)1881 年成为美国第 20 任总统
1876 年提出有关证明aabbcc∟∟∟你还有其他证明方法吗?求下列图中字母所表示的正方形的面积=625=144 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7cm,求正方形A,B,C,D的面积的和S1S2解:∵ SE= 49S1=SA+SBS2=SC+SD∴ SA+SB+SC+SD
= S1+S2 = SE = 49美丽的勾股树(一)美丽的勾股树(二)挑战自我1、本节课我们经历了怎样的过程? 经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。3、学了本节课后我们有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。同学们,想一想,这节课你有什么收获?思考题:一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少? AB0当木梯顶端下滑0.5米,这时梯脚与墙的距离是否向右滑动0.5米?2.52.4CD0.50.5 ?再见观察下列表格:……请你结合该表格及相关知识,求出b、c的值.
即b= ,c= 。
8485阿满想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗? ABC5米(x+1)米x米DA蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE(2004年中考·黄冈)如图所示,是一种“羊头”形图案,其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②′,…,依次类推,若正方形①的边长为64cm,则正方形⑦的边长为_________cm.
受台风麦莎影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
1876 年提出有关证明aabbcc∟∟∟你还有其他证明方法吗?求下列图中字母所表示的正方形的面积=625=144 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7cm,求正方形A,B,C,D的面积的和S1S2解:∵ SE= 49S1=SA+SBS2=SC+SD∴ SA+SB+SC+SD
= S1+S2 = SE = 49美丽的勾股树(一)美丽的勾股树(二)挑战自我1、本节课我们经历了怎样的过程? 经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。3、学了本节课后我们有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。同学们,想一想,这节课你有什么收获?思考题:一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少? AB0当木梯顶端下滑0.5米,这时梯脚与墙的距离是否向右滑动0.5米?2.52.4CD0.50.5 ?再见观察下列表格:……请你结合该表格及相关知识,求出b、c的值.
即b= ,c= 。
8485阿满想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗? ABC5米(x+1)米x米DA蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE(2004年中考·黄冈)如图所示,是一种“羊头”形图案,其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②′,…,依次类推,若正方形①的边长为64cm,则正方形⑦的边长为_________cm.
受台风麦莎影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
