3.1.2 等式的性质课件
文档属性
| 名称 | 3.1.2 等式的性质课件 |  | |
| 格式 | zip | ||
| 文件大小 | 980.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-22 09:48:10 | ||
图片预览




文档简介
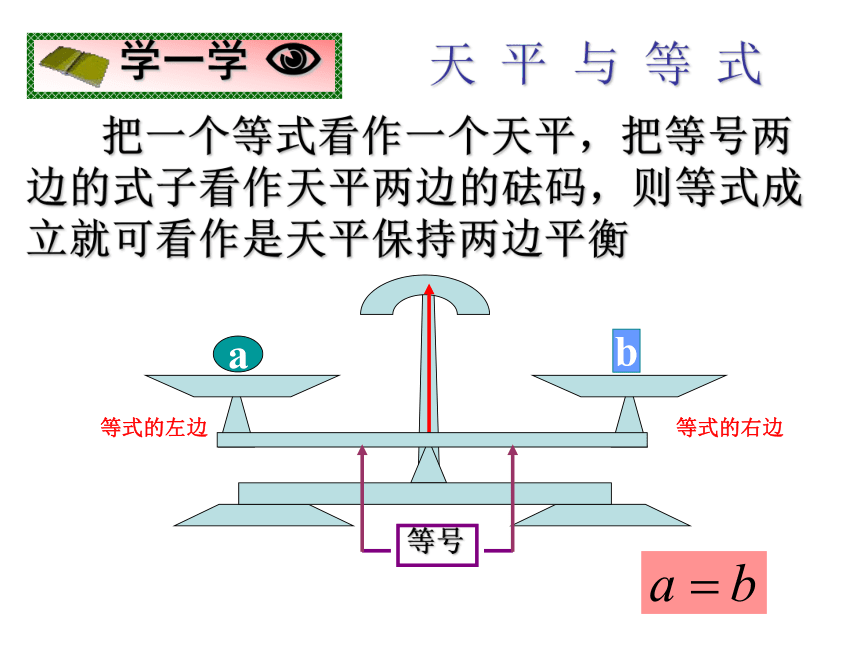
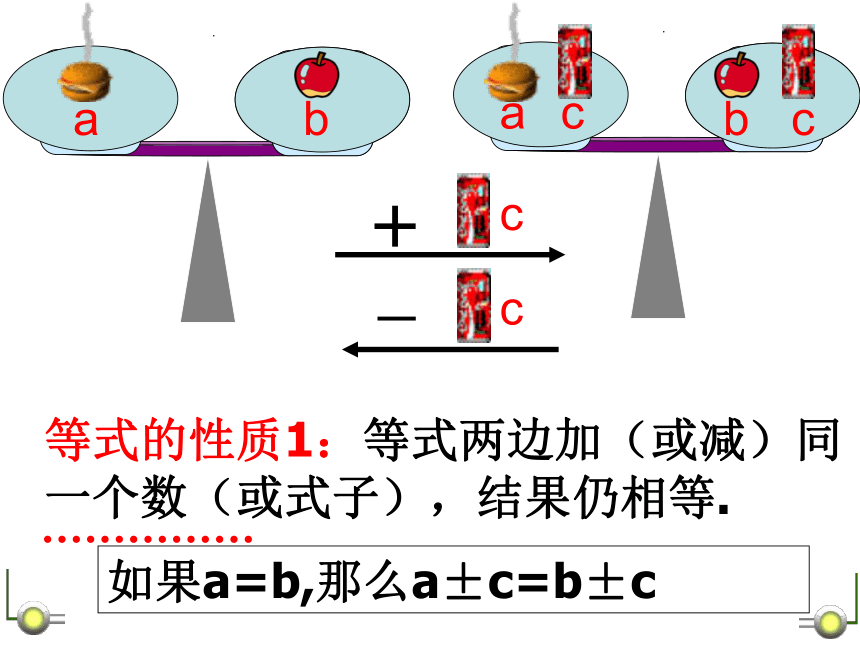
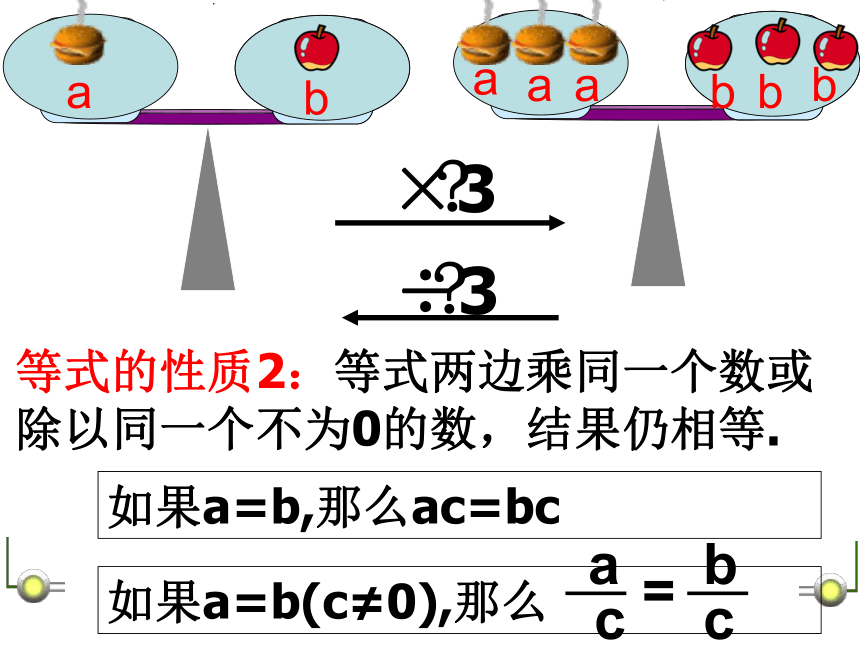
课件19张PPT。等式的性质这是什么?ba天 平 与 等 式 把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡等式的左边等式的右边+—等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.如果a=b,那么a±c=b±c等式的性质2:等式两边乘同一个数或除以同一个不为0的数,结果仍相等.×3÷3??如果a=b,那么ac=bc如果a=b(c≠0),那么等 式 的 性 质【等式性质 2 】【等式性质1】【例1】用等式的性质回答下列各题
(1) 从x=y能不能得到x+5=y+5呢?为什么?
(2)从a+2=b+2能不能得到a=b呢?为什么?
(3)从-3a=-3b能不能得到a=b呢?为什么?
(4)从x=y能不能得到 呢?为什么?
(5)从x=y能否得到 呢?为什么?
(6)从x=y能否得到 呢?为什么?
能,等式的性质1能,等式的性质1能,等式的性质2能,等式的性质2不能,因不确定a是否为0能,等式的性质2判断对错:
对的说明根据等式的哪一条性质;错的说出为什么。×√××√×注意:除以同一个不为0的数√D D在下面的括号内填上适当的数或代数式(1)因为 : x – 6 = 4
所以 : x – 6 + 6 = 4 + ( )
即: x = ( )(2)因为: 3x = 2x – 8
所以: 3x –( ) = 2x – 8 – 2x
即: x = ( )6102x-8(因为x可能等于0)(等量代换)(对称性)×√√ 经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的形式:
x = a(常数)
即方程左边只一个未知数项、且未知数项的系数是 1,右边只一个常数项.解下列方程:思考:(1)每一步的依据分别是什么?
(2)求方程的解就是把方程化成什么形式?解:(1)两边减7得:
化简,得:
(2)两边除以2得:
化简得:等式的性质1或2化成x=a的形式例:利用等式的性质解方程:(1)解:两边减0.6得: 化简,得: 两边同乘-1得:小结:(1)这个方程的解答中两次运用了等式的性质;
(2)解方程的目标是把方程最终化为 的形式,在运用等式性质进行变形时,始终要朝着这个目标去转化。(2)解:两边加5 得: 化简,得: 两边同乘-3得:思考:(1)第2题能否先在方程的两边同乘-3?
(2)你认为哪种方法更好,为什么?
(3) 是方程(2)的解吗?【例2】用等式的性质解下列方程(1)解:两边减2得:
化简,得:
两边乘-2得:(2)解:两边减2得:
化简,得:
两边除以-3得:
利用等式的基本性质解下列方程(3) 解:两边加5,得
化简,得
两边同乘 (-3),得m - 5= 4你会检验吗?我会应用 (3)、如果4x=-12y,那么x= , 根据 。 (4)、如果-0.2x=6,那么x= , 根据 。(2)、如果x-3=2,那么x-3+3= ,2x0.5等式性质2,在等式两边同时乘2等式性质1,在等式两边同加32+3-3y等式性质2,在等式两边同时除以4-30等式性质2,在等式两边同除以-0.2或乘-5我来当法官! 在学习了等式的性质后,小红发现运用等式的性质可以使复杂的等式变得简洁,这使她异常兴奋,于是她随手写了一个等式:3a+b-2=7a+b-2,并开始运用等式性质对这个等式进行变形,其过程如下:
3a+b=7a+b(等式两边同时加上2)
3a=7a(等式两边同时减去b)
3=7(等式两边同时除以a)
变形到此,小红顿时就傻了:居然得出如此等式!于是小红开始检查自己的变形过程,但怎么也找不出错误来。
聪明的同学,你能让小红的愁眉在恍然大悟中舒展开来吗?
(1) 从x=y能不能得到x+5=y+5呢?为什么?
(2)从a+2=b+2能不能得到a=b呢?为什么?
(3)从-3a=-3b能不能得到a=b呢?为什么?
(4)从x=y能不能得到 呢?为什么?
(5)从x=y能否得到 呢?为什么?
(6)从x=y能否得到 呢?为什么?
能,等式的性质1能,等式的性质1能,等式的性质2能,等式的性质2不能,因不确定a是否为0能,等式的性质2判断对错:
对的说明根据等式的哪一条性质;错的说出为什么。×√××√×注意:除以同一个不为0的数√D D在下面的括号内填上适当的数或代数式(1)因为 : x – 6 = 4
所以 : x – 6 + 6 = 4 + ( )
即: x = ( )(2)因为: 3x = 2x – 8
所以: 3x –( ) = 2x – 8 – 2x
即: x = ( )6102x-8(因为x可能等于0)(等量代换)(对称性)×√√ 经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的形式:
x = a(常数)
即方程左边只一个未知数项、且未知数项的系数是 1,右边只一个常数项.解下列方程:思考:(1)每一步的依据分别是什么?
(2)求方程的解就是把方程化成什么形式?解:(1)两边减7得:
化简,得:
(2)两边除以2得:
化简得:等式的性质1或2化成x=a的形式例:利用等式的性质解方程:(1)解:两边减0.6得: 化简,得: 两边同乘-1得:小结:(1)这个方程的解答中两次运用了等式的性质;
(2)解方程的目标是把方程最终化为 的形式,在运用等式性质进行变形时,始终要朝着这个目标去转化。(2)解:两边加5 得: 化简,得: 两边同乘-3得:思考:(1)第2题能否先在方程的两边同乘-3?
(2)你认为哪种方法更好,为什么?
(3) 是方程(2)的解吗?【例2】用等式的性质解下列方程(1)解:两边减2得:
化简,得:
两边乘-2得:(2)解:两边减2得:
化简,得:
两边除以-3得:
利用等式的基本性质解下列方程(3) 解:两边加5,得
化简,得
两边同乘 (-3),得m - 5= 4你会检验吗?我会应用 (3)、如果4x=-12y,那么x= , 根据 。 (4)、如果-0.2x=6,那么x= , 根据 。(2)、如果x-3=2,那么x-3+3= ,2x0.5等式性质2,在等式两边同时乘2等式性质1,在等式两边同加32+3-3y等式性质2,在等式两边同时除以4-30等式性质2,在等式两边同除以-0.2或乘-5我来当法官! 在学习了等式的性质后,小红发现运用等式的性质可以使复杂的等式变得简洁,这使她异常兴奋,于是她随手写了一个等式:3a+b-2=7a+b-2,并开始运用等式性质对这个等式进行变形,其过程如下:
3a+b=7a+b(等式两边同时加上2)
3a=7a(等式两边同时减去b)
3=7(等式两边同时除以a)
变形到此,小红顿时就傻了:居然得出如此等式!于是小红开始检查自己的变形过程,但怎么也找不出错误来。
聪明的同学,你能让小红的愁眉在恍然大悟中舒展开来吗?
