活动单导学课程 苏教版高中数学选择性必修第一册第5章导数及其应用5.3.3 最大值与最小值(1)(有答案
文档属性
| 名称 | 活动单导学课程 苏教版高中数学选择性必修第一册第5章导数及其应用5.3.3 最大值与最小值(1)(有答案 |
|
|
| 格式 | docx | ||
| 文件大小 | 124.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-29 20:54:19 | ||
图片预览



文档简介
5.3.3 最大值与最小值(1)
1. 理解最值的概念,掌握极值与最值的联系与区别.
2. 能熟练、准确地求函数的最值.
3. 初步掌握解决与最值有关的求参、恒成立、方程根、函数图象等问题的方法.
活动一 掌握最值的概念,理解极值与最值的联系与区别
1. (1) 复习巩固:极值的概念与极值的求法:
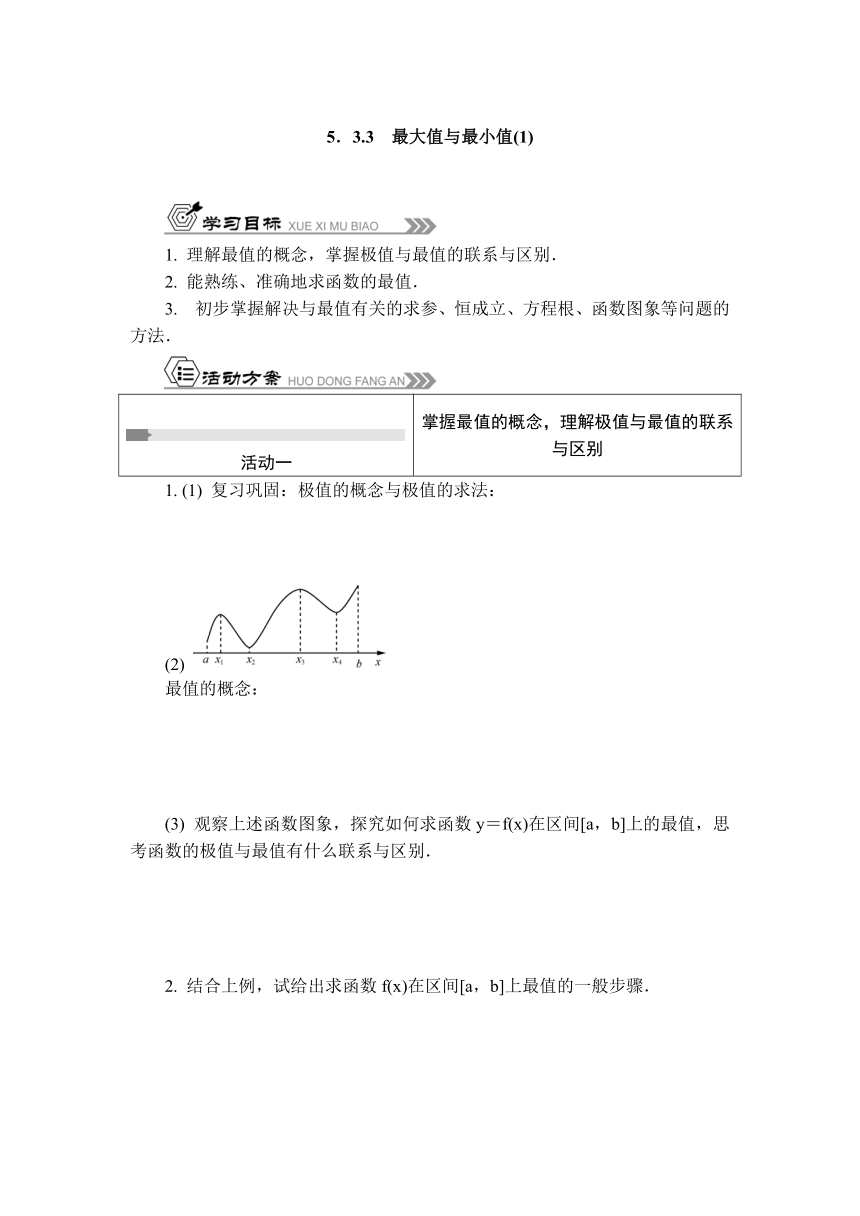
(2)
最值的概念:
(3) 观察上述函数图象,探究如何求函数y=f(x)在区间[a,b]上的最值,思考函数的极值与最值有什么联系与区别.
2. 结合上例,试给出求函数f(x)在区间[a,b]上最值的一般步骤.
活动二 掌握求函数最值的方法
例1 求函数f(x)=x2-4x+3在区间[-1,4]上的最大值与最小值.
思考1
若将区间[-1,4]改为区间(-1,4),结果会怎样?
例2 求函数f(x)=x+sinx在区间[0,2π]上的最大值与最小值.
思考2
试根据上述求解过程,作出函数f(x)=x+sinx 在区间[0,2π]上的大致图象.
活动三 掌握与函数最值有关的参数的取值范围问题
例3 已知函数f(x)=ax3-6ax2+b,是否存在实数a,b,使函数f(x)在区间[-1,2]上取得最大值3,最小值-29?若存在,求出a,b的值;若不存在,请说明理由.
例4 设函数f(x)=3x2+(x>0),?x∈(0,+∞),f(x)≥20恒成立,求正实数a的取值范围.
1. 函数f(x)=x3-3x2+2在区间[-1,1]上的最大值是( )
A. -2 B. 0 C. 2 D. 4
2. 函数y=x·lnx的最小值为( )
A. e B. -e C. - D.
3. (多选)下列结论中,正确的是( )
A. f(x)=x+(x∈R)的最小值为1
B. f(x)=(x>0)的最小值为1
C. f(x)=x-ln x(x>0)的最小值为1
D. f(x)=xe(x>0)的最小值1
4. 函数f(x)=(x+1)ex的最小值是________.
5. 已知函数f(x)=x3+3x2-9x.
(1) 求曲线f(x)在点(1,-5)处的切线方程;
(2) 求函数f(x)在区间[-1,2]上的最小值和最大值.
参考答案与解析
【活动方案】
1. (1) 略
(2) 最值的概念:如果在定义域I内存在x0,使得对任意的x∈I,总有f(x)≤f(x0)(f(x)≥f(x0)),那么f(x0)为函数在定义域上的最大值(最小值).
(3) 观察函数图象可知,f(x1),f(x3)是极大值,而f(b)>f(x3)>f(x1),所以f(b)是最大值;
f(x2),f(x4)是极小值,而f(x2)联系:若函数f(x)在区间[a,b]上是连续的,其最值只能在极值点或端点处取得.
区别:最值是整体概念,极值是局部概念.
2. ①求函数f(x)在区间(a,b)上的极值;
②将求得的极值与f(a),f(b)比较,得到f(x)在区间[a,b]上的最大值与最小值.
例1 由f′(x)=2x-4=0,得x=2.列表如下:
x -1 (-1,2) 2 (2,4) 4
f′(x) - 0 +
f(x) 8 ?↘ -1 ?↗ 3
由上表可知,函数f(x)在区间[-1,4]上的最大值是8,最小值是-1.
思考1:无最大值,最小值是-1.
例2 由f′(x)=+cosx=0,x∈[0,2π],得x1=,x2=.列表如下:
x 0 (0,) (,) (,2π) 2π
f′(x) + 0 - 0 +
f(x) 0 ↗? + ↘? - ?↗ π
由上表可知,函数f(x)在区间[0,2π]上的最大值是π,最小值是0.
思考2:
例3 显然a=0不符合题意.
f′(x)=3ax2-12ax=3ax(x-4).
①若a>0,由f′(x)>0,得x<0或x>4,
所以函数f(x)在区间[-1,0]上单调递增,在区间(0,2]上单调递减,
所以f(x)max=f(0)=b=3.
又f(-1)=3-7a,f(2)=3-16a,
所以f(x)min=f(2)=3-16a=-29,
解得a=2;
②若a<0,由f′(x)>0,得0所以函数f(x)在区间[-1,0]上单调递减,在区间(0,2]上单调递增,
所以f(x)min=f(0)=b=-29.
又f(-1)=-7a-29,f(2)=-16a-29,
所以f(x)max=f(2)=-16a-29=3,
解得a=-2.
综上,a=2,b=3或a=-2,b=-29.
例4 由题意,得3x2+≥20在区间(0,+∞)上恒成立,即a≥x3(20-3x2)在区间(0,+∞)上恒成立.
令h(x)=20x3-3x5,x>0,
则h′(x)=60x2-15x4.
由h′(x)>0,得-2所以函数h(x)在区间(0,2)上单调递增,在区间(2,+∞)上单调递减,
所以h(x)max=h(2)=20×23-3×25=64,
所以a≥64.
综上,正实数a的取值范围是[64,+∞).
【检测反馈】
1. C 解析:由f′(x)=3x2-6x>0,得x<0或x>2,所以函数f(x)在区间[-1,0)上单调递增,在区间[0,1]上单调递减,所以f(x)max=f(0)=2.
2. C 解析:由题意,得y′=lnx+1.由y′=lnx+1>0,得x>;由y′=lnx+1<0,得03. AC 解析:对于A,f(x)=x+(x∈R),则f′(x)=1-=,所以函数f(x)在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增,故函数f(x)的最小值为f(0)=1,故A正确;对于B,f(x)=(x>0),则f′(x)=,所以函数f(x)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,故函数f(x)的最小值为f(1)=e,故B错误;对于C,f(x)=x-ln x(x>0),则f′(x)=1-=,所以函数f(x)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,故函数f(x)的最小值为f(1)=1,故C正确;对于D,f(x)=xe(x>0),则f′(x)=e+x·e·=,所以函数f(x)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,故函数f(x)的最小值为f(1)=e,故D错误.故选AC.
4. - 解析:由题意,得f′(x)=(x+2)ex,当x>-2时,f′(x)>0,函数f(x)单调递增;当x<-2时,f′(x)<0,函数f(x)单调递减,所以当x=-2时,函数取得极小值也是最小值,最小值为f(-2)=(-2+1)e-2=-.
5. (1) 因为f(x)=x3+3x2-9x,
所以f′(x)=3x2+6x-9,
所以f′(1)=0,f(1)=-5,
所以曲线y=f(x)在点(1,-5)处的切线方程为y=-5.
(2) 令f′(x)=3(x2+2x-3)=0,解得x=-3(舍去)或x=1.
列表如下:
x [-1,1) 1 (1,2]
f′(x) - 0 +
f(x) ↘? 极小值 ?↗
所以函数f(x)在区间[-1,1)上单调递减,在区间(1,2]上单调递增,
所以函数f(x)的极小值为f(1)=-5.
又f(-1)=-1+3+9=11,f(2)=23+3×22-9×2=2,
所以函数f(x)在区间[-1,2]上的最小值为-5,最大值为11.
1. 理解最值的概念,掌握极值与最值的联系与区别.
2. 能熟练、准确地求函数的最值.
3. 初步掌握解决与最值有关的求参、恒成立、方程根、函数图象等问题的方法.
活动一 掌握最值的概念,理解极值与最值的联系与区别
1. (1) 复习巩固:极值的概念与极值的求法:
(2)
最值的概念:
(3) 观察上述函数图象,探究如何求函数y=f(x)在区间[a,b]上的最值,思考函数的极值与最值有什么联系与区别.
2. 结合上例,试给出求函数f(x)在区间[a,b]上最值的一般步骤.
活动二 掌握求函数最值的方法
例1 求函数f(x)=x2-4x+3在区间[-1,4]上的最大值与最小值.
思考1
若将区间[-1,4]改为区间(-1,4),结果会怎样?
例2 求函数f(x)=x+sinx在区间[0,2π]上的最大值与最小值.
思考2
试根据上述求解过程,作出函数f(x)=x+sinx 在区间[0,2π]上的大致图象.
活动三 掌握与函数最值有关的参数的取值范围问题
例3 已知函数f(x)=ax3-6ax2+b,是否存在实数a,b,使函数f(x)在区间[-1,2]上取得最大值3,最小值-29?若存在,求出a,b的值;若不存在,请说明理由.
例4 设函数f(x)=3x2+(x>0),?x∈(0,+∞),f(x)≥20恒成立,求正实数a的取值范围.
1. 函数f(x)=x3-3x2+2在区间[-1,1]上的最大值是( )
A. -2 B. 0 C. 2 D. 4
2. 函数y=x·lnx的最小值为( )
A. e B. -e C. - D.
3. (多选)下列结论中,正确的是( )
A. f(x)=x+(x∈R)的最小值为1
B. f(x)=(x>0)的最小值为1
C. f(x)=x-ln x(x>0)的最小值为1
D. f(x)=xe(x>0)的最小值1
4. 函数f(x)=(x+1)ex的最小值是________.
5. 已知函数f(x)=x3+3x2-9x.
(1) 求曲线f(x)在点(1,-5)处的切线方程;
(2) 求函数f(x)在区间[-1,2]上的最小值和最大值.
参考答案与解析
【活动方案】
1. (1) 略
(2) 最值的概念:如果在定义域I内存在x0,使得对任意的x∈I,总有f(x)≤f(x0)(f(x)≥f(x0)),那么f(x0)为函数在定义域上的最大值(最小值).
(3) 观察函数图象可知,f(x1),f(x3)是极大值,而f(b)>f(x3)>f(x1),所以f(b)是最大值;
f(x2),f(x4)是极小值,而f(x2)
区别:最值是整体概念,极值是局部概念.
2. ①求函数f(x)在区间(a,b)上的极值;
②将求得的极值与f(a),f(b)比较,得到f(x)在区间[a,b]上的最大值与最小值.
例1 由f′(x)=2x-4=0,得x=2.列表如下:
x -1 (-1,2) 2 (2,4) 4
f′(x) - 0 +
f(x) 8 ?↘ -1 ?↗ 3
由上表可知,函数f(x)在区间[-1,4]上的最大值是8,最小值是-1.
思考1:无最大值,最小值是-1.
例2 由f′(x)=+cosx=0,x∈[0,2π],得x1=,x2=.列表如下:
x 0 (0,) (,) (,2π) 2π
f′(x) + 0 - 0 +
f(x) 0 ↗? + ↘? - ?↗ π
由上表可知,函数f(x)在区间[0,2π]上的最大值是π,最小值是0.
思考2:
例3 显然a=0不符合题意.
f′(x)=3ax2-12ax=3ax(x-4).
①若a>0,由f′(x)>0,得x<0或x>4,
所以函数f(x)在区间[-1,0]上单调递增,在区间(0,2]上单调递减,
所以f(x)max=f(0)=b=3.
又f(-1)=3-7a,f(2)=3-16a,
所以f(x)min=f(2)=3-16a=-29,
解得a=2;
②若a<0,由f′(x)>0,得0
所以f(x)min=f(0)=b=-29.
又f(-1)=-7a-29,f(2)=-16a-29,
所以f(x)max=f(2)=-16a-29=3,
解得a=-2.
综上,a=2,b=3或a=-2,b=-29.
例4 由题意,得3x2+≥20在区间(0,+∞)上恒成立,即a≥x3(20-3x2)在区间(0,+∞)上恒成立.
令h(x)=20x3-3x5,x>0,
则h′(x)=60x2-15x4.
由h′(x)>0,得-2
所以h(x)max=h(2)=20×23-3×25=64,
所以a≥64.
综上,正实数a的取值范围是[64,+∞).
【检测反馈】
1. C 解析:由f′(x)=3x2-6x>0,得x<0或x>2,所以函数f(x)在区间[-1,0)上单调递增,在区间[0,1]上单调递减,所以f(x)max=f(0)=2.
2. C 解析:由题意,得y′=lnx+1.由y′=lnx+1>0,得x>;由y′=lnx+1<0,得0
4. - 解析:由题意,得f′(x)=(x+2)ex,当x>-2时,f′(x)>0,函数f(x)单调递增;当x<-2时,f′(x)<0,函数f(x)单调递减,所以当x=-2时,函数取得极小值也是最小值,最小值为f(-2)=(-2+1)e-2=-.
5. (1) 因为f(x)=x3+3x2-9x,
所以f′(x)=3x2+6x-9,
所以f′(1)=0,f(1)=-5,
所以曲线y=f(x)在点(1,-5)处的切线方程为y=-5.
(2) 令f′(x)=3(x2+2x-3)=0,解得x=-3(舍去)或x=1.
列表如下:
x [-1,1) 1 (1,2]
f′(x) - 0 +
f(x) ↘? 极小值 ?↗
所以函数f(x)在区间[-1,1)上单调递减,在区间(1,2]上单调递增,
所以函数f(x)的极小值为f(1)=-5.
又f(-1)=-1+3+9=11,f(2)=23+3×22-9×2=2,
所以函数f(x)在区间[-1,2]上的最小值为-5,最大值为11.
