18.1 勾股定理(3)[下学期]
文档属性
| 名称 | 18.1 勾股定理(3)[下学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 163.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-17 00:00:00 | ||
图片预览



文档简介
(共40张PPT)
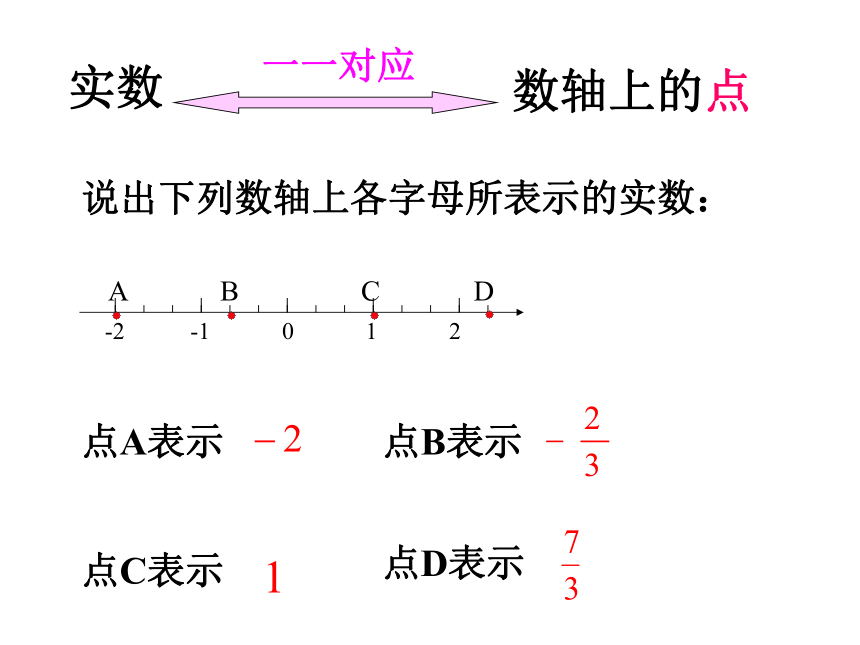
实数
数轴上的点
一一对应
说出下列数轴上各字母所表示的实数:
A B C D
-2 -1 0 1 2
点C表示
点D表示
点B表示
点A表示
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上表示出 的点吗?
0
1
2
3
4
步骤:
l
A
B
C
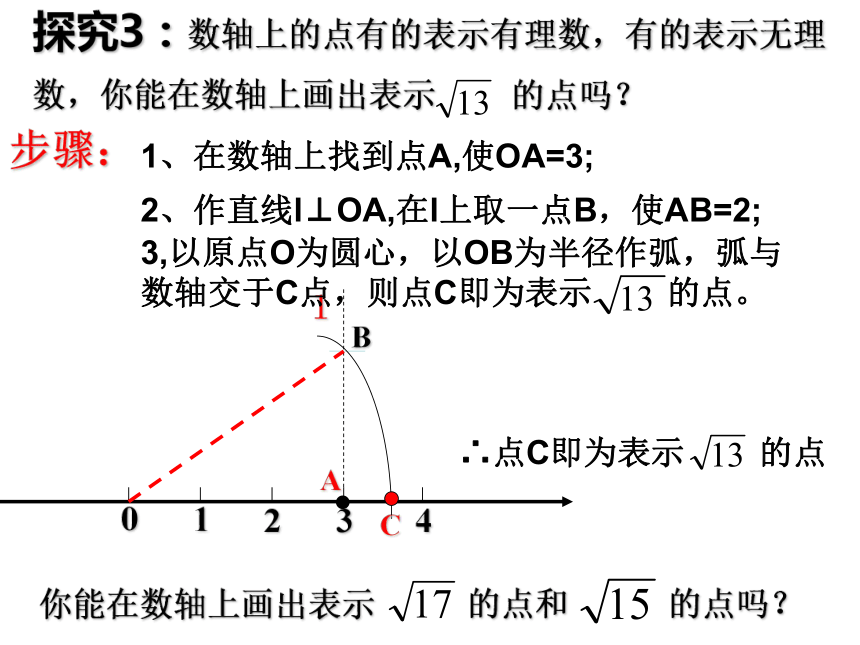
1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
3,以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。
探究3:数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
你能在数轴上画出表示 的点和 的点吗?
∴点C即为表示 的点
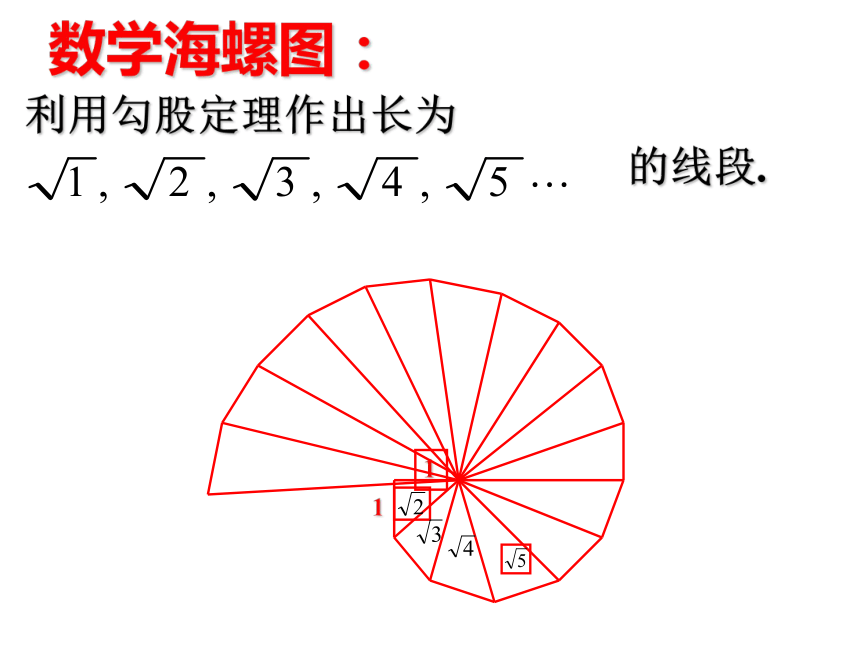
数学海螺图:
利用勾股定理作出长为
的线段.
1
1
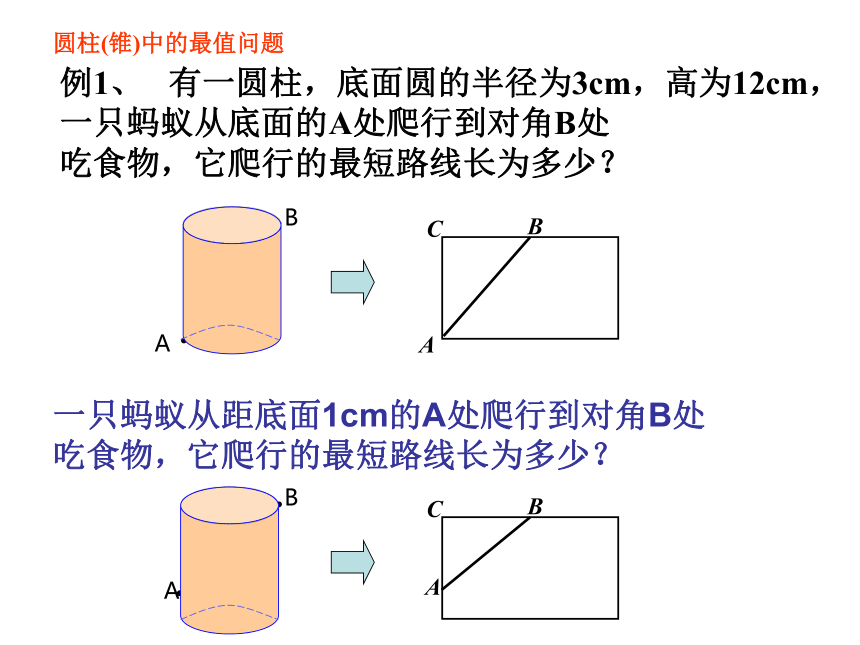
圆柱(锥)中的最值问题
例1、 有一圆柱,底面圆的半径为3cm,高为12cm,一只蚂蚁从底面的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?
A
B
B
A
C
一只蚂蚁从距底面1cm的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?
A
B
B
A
C
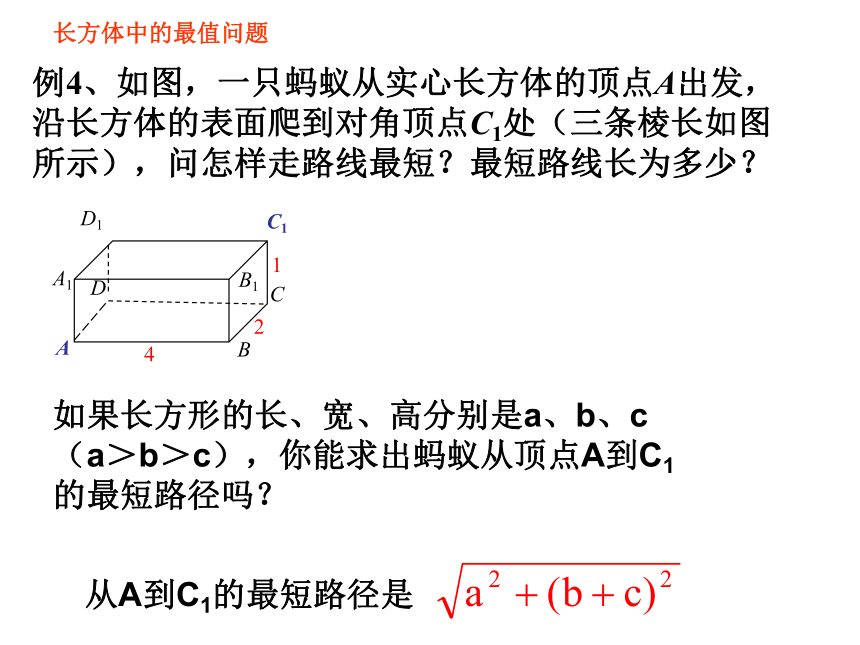
例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
长方体中的最值问题
如果长方形的长、宽、高分别是a、b、c(a>b>c),你能求出蚂蚁从顶点A到C1的最短路径吗?
从A到C1的最短路径是
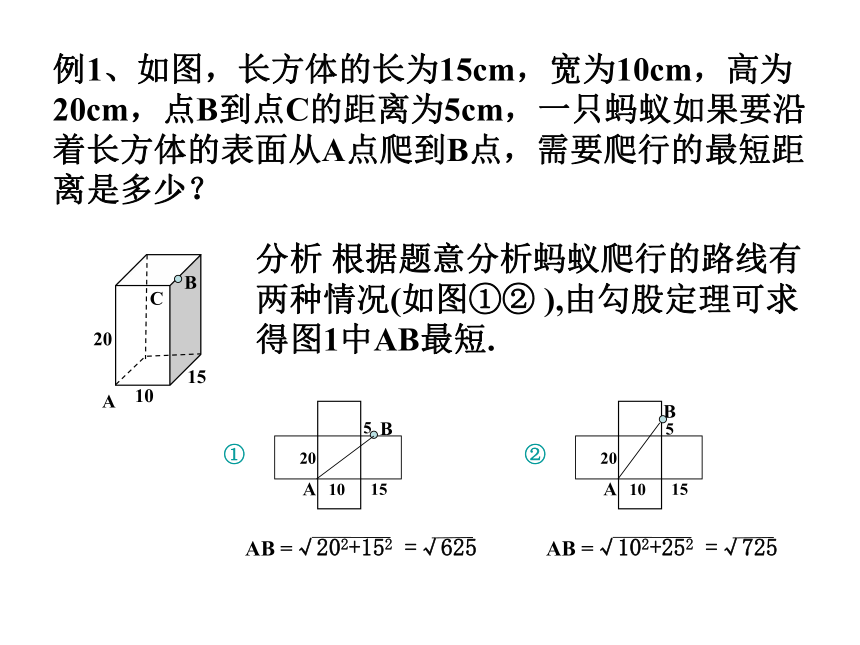
例1、如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离为5cm,一只蚂蚁如果要沿着长方体的表面从A点爬到B点,需要爬行的最短距离是多少?
20
10
15
B
C
A
分析 根据题意分析蚂蚁爬行的路线有两种情况(如图①② ),由勾股定理可求得图1中AB最短.
①
B
A
20
10
15
5
AB =√202+152 =√625
B
AB =√102+252 =√725
②
A
20
10
15
5
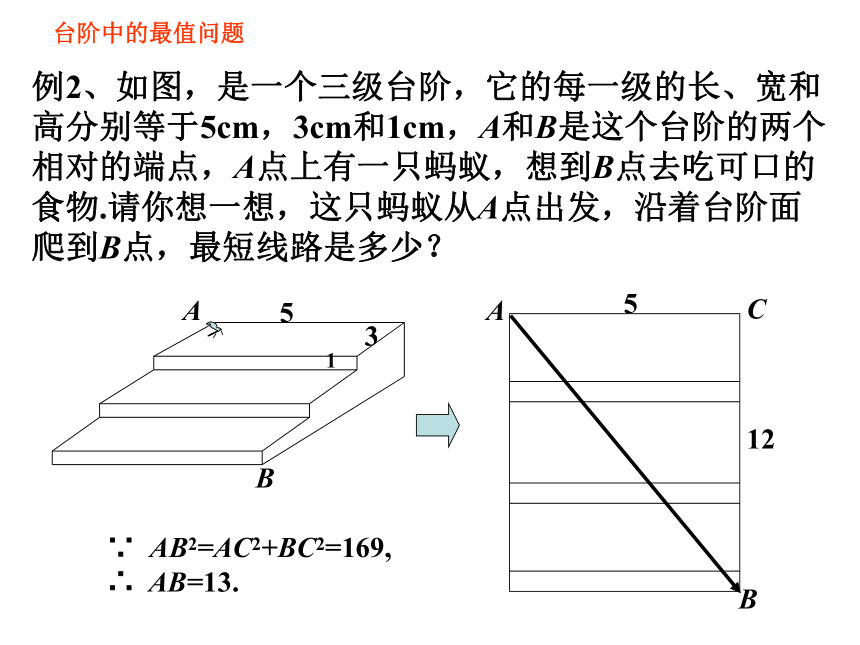
例2、如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
5
3
1
5
12
台阶中的最值问题
∵ AB2=AC2+BC2=169,
∴ AB=13.
D
A
B
C
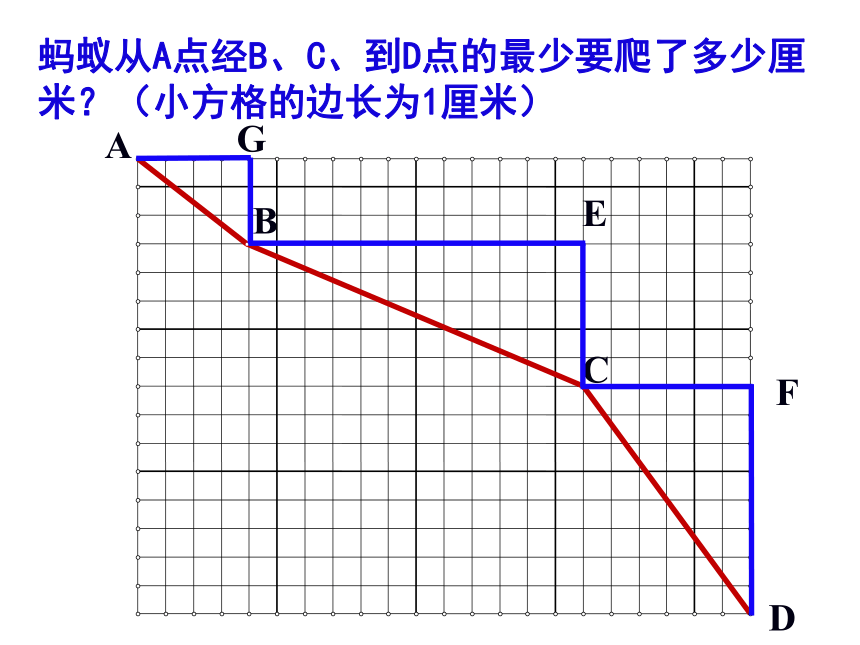
蚂蚁从A点经B、C、到D点的最少要爬了多少厘米?(小方格的边长为1厘米)
G
F
E
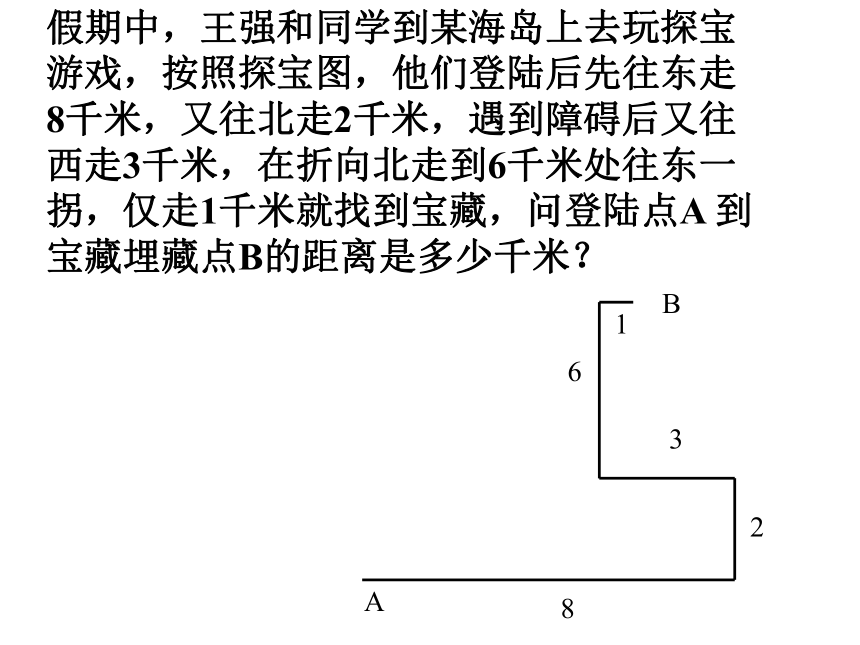
假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,在折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏埋藏点B的距离是多少千米?
A
B
8
2
3
6
1
小溪边长着两棵树,恰好隔岸相望,一棵树高30尺,另外一棵树高20尺;两棵树干间的距离是50尺,每棵树上都停着一只鸟,忽然两只鸟同时看到两树间水面上游出一条鱼,它们立刻以同样的速度飞去抓鱼,结果同时到达目标。问这条鱼出现在两树之间的何处?
如图,等边三角形的边长是2。
(1)求高AD的长;
(2)求这个三角形的面积。
A
B
D
C
若等边三角形的边长是a呢?
如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积。
A
B
C
15
14
13
如图,在△ABC中,∠ACB=900,AB=50cm,BC=30cm,CD⊥AB于D,求CD的长。
A
B
C
D
已知,一轮船以16海里/时的速度从港口A出发向西北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东北方向航行,离开港口2小时后,则两船相距( )
A、25海里 B、30海里
C、35海里 D、40海里
一个圆柱状的杯子,由内部测得其底面直径为4cm,高为10cm,现有一支12cm的吸管任意斜放于杯中,则吸管 _露出杯口外. (填“能”或“不能”)
1、放学以后,小红和小颖从学校分手,分别沿着东方向和南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米 B、800米
C、1000米 D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米 B、 8厘米
C、 80/13厘米; D、 60/13厘米;
C
D
例2:
如图,求矩形零件上两孔中心A、B的距离.
21
21
40
60
A
B
C
(一)、
折叠四边形
例1:折叠矩形纸片,先折出折痕对角线BD,在绕点D折叠,使点A落在BD的E处,折痕DG,若AB=2,BC=1,求AG的长。
D
A
G
B
C
E
例2:矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。
A
B
C
D
F
E
例3:矩形ABCD中,AB=6,BC=8,先把它对折,折痕为EF,展开后再沿BG折叠,使A落在EF上的A1,求第二次折痕BG的长。
A
B
C
D
E
F
A1
G
正三角形AA1B
例4:边长为8和4的矩形OABC的两边分别在直角坐标系的X轴和Y轴上,若 沿对角线AC折叠后,点B落在第四象限B1处,设B1C交X轴于点D,求(1)三角形ADC的面积,(2)点B1的坐标,(3)AB1所在的直线解析式。
O
C
B
A
B1
D
1
2
3
E
(二)
折叠三角形
例1、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
例2:三角形ABC是等腰三角形AB=AC=13,BC=10,将AB向AC方向对折,再将CD折叠到CA边上,折痕CE,求三角形ACE的面积
A
B
C
D
A
D
C
D
C
A
D1
E
勾股定理的拓展训 练
三
1.如图,在四边形ABCD中,∠BAD =900,∠DBC = 900 , AD = 3,AB = 4,BC = 12, 求CD;
A
B
C
D
2.已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四边形ABCD的面积。
3、在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。
A
B
C
D
13
13
10
H
提示:利用面积相等的关系
4、 已知等边三角形ABC的边长是6cm,(1)求高AD的长;(2)S△ABC
A
B
C
D
解:(1)
∵△ABC是等边三角形,AD是高
在Rt△ABD中
,根据勾股定理
5、 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。
解:
∵∠ABD=90°,∠DAB=30°
∴BD= AD=4
在Rt△ABD中
,根据勾股定理
在Rt△ABC中,
又AD=8
A
B
C
D
30°
8
6、 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD
A
B
C
D
证明:
过A作AE⊥BC于E
E
∵AB=AC,∴BE=CE
在Rt △ADE中,
AD2=AE2+DE2
在Rt △ABE中,
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD
实数
数轴上的点
一一对应
说出下列数轴上各字母所表示的实数:
A B C D
-2 -1 0 1 2
点C表示
点D表示
点B表示
点A表示
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上表示出 的点吗?
0
1
2
3
4
步骤:
l
A
B
C
1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
3,以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。
探究3:数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
你能在数轴上画出表示 的点和 的点吗?
∴点C即为表示 的点
数学海螺图:
利用勾股定理作出长为
的线段.
1
1
圆柱(锥)中的最值问题
例1、 有一圆柱,底面圆的半径为3cm,高为12cm,一只蚂蚁从底面的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?
A
B
B
A
C
一只蚂蚁从距底面1cm的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?
A
B
B
A
C
例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
长方体中的最值问题
如果长方形的长、宽、高分别是a、b、c(a>b>c),你能求出蚂蚁从顶点A到C1的最短路径吗?
从A到C1的最短路径是
例1、如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离为5cm,一只蚂蚁如果要沿着长方体的表面从A点爬到B点,需要爬行的最短距离是多少?
20
10
15
B
C
A
分析 根据题意分析蚂蚁爬行的路线有两种情况(如图①② ),由勾股定理可求得图1中AB最短.
①
B
A
20
10
15
5
AB =√202+152 =√625
B
AB =√102+252 =√725
②
A
20
10
15
5
例2、如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
5
3
1
5
12
台阶中的最值问题
∵ AB2=AC2+BC2=169,
∴ AB=13.
D
A
B
C
蚂蚁从A点经B、C、到D点的最少要爬了多少厘米?(小方格的边长为1厘米)
G
F
E
假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,在折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏埋藏点B的距离是多少千米?
A
B
8
2
3
6
1
小溪边长着两棵树,恰好隔岸相望,一棵树高30尺,另外一棵树高20尺;两棵树干间的距离是50尺,每棵树上都停着一只鸟,忽然两只鸟同时看到两树间水面上游出一条鱼,它们立刻以同样的速度飞去抓鱼,结果同时到达目标。问这条鱼出现在两树之间的何处?
如图,等边三角形的边长是2。
(1)求高AD的长;
(2)求这个三角形的面积。
A
B
D
C
若等边三角形的边长是a呢?
如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积。
A
B
C
15
14
13
如图,在△ABC中,∠ACB=900,AB=50cm,BC=30cm,CD⊥AB于D,求CD的长。
A
B
C
D
已知,一轮船以16海里/时的速度从港口A出发向西北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东北方向航行,离开港口2小时后,则两船相距( )
A、25海里 B、30海里
C、35海里 D、40海里
一个圆柱状的杯子,由内部测得其底面直径为4cm,高为10cm,现有一支12cm的吸管任意斜放于杯中,则吸管 _露出杯口外. (填“能”或“不能”)
1、放学以后,小红和小颖从学校分手,分别沿着东方向和南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米 B、800米
C、1000米 D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米 B、 8厘米
C、 80/13厘米; D、 60/13厘米;
C
D
例2:
如图,求矩形零件上两孔中心A、B的距离.
21
21
40
60
A
B
C
(一)、
折叠四边形
例1:折叠矩形纸片,先折出折痕对角线BD,在绕点D折叠,使点A落在BD的E处,折痕DG,若AB=2,BC=1,求AG的长。
D
A
G
B
C
E
例2:矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。
A
B
C
D
F
E
例3:矩形ABCD中,AB=6,BC=8,先把它对折,折痕为EF,展开后再沿BG折叠,使A落在EF上的A1,求第二次折痕BG的长。
A
B
C
D
E
F
A1
G
正三角形AA1B
例4:边长为8和4的矩形OABC的两边分别在直角坐标系的X轴和Y轴上,若 沿对角线AC折叠后,点B落在第四象限B1处,设B1C交X轴于点D,求(1)三角形ADC的面积,(2)点B1的坐标,(3)AB1所在的直线解析式。
O
C
B
A
B1
D
1
2
3
E
(二)
折叠三角形
例1、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
例2:三角形ABC是等腰三角形AB=AC=13,BC=10,将AB向AC方向对折,再将CD折叠到CA边上,折痕CE,求三角形ACE的面积
A
B
C
D
A
D
C
D
C
A
D1
E
勾股定理的拓展训 练
三
1.如图,在四边形ABCD中,∠BAD =900,∠DBC = 900 , AD = 3,AB = 4,BC = 12, 求CD;
A
B
C
D
2.已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四边形ABCD的面积。
3、在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。
A
B
C
D
13
13
10
H
提示:利用面积相等的关系
4、 已知等边三角形ABC的边长是6cm,(1)求高AD的长;(2)S△ABC
A
B
C
D
解:(1)
∵△ABC是等边三角形,AD是高
在Rt△ABD中
,根据勾股定理
5、 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。
解:
∵∠ABD=90°,∠DAB=30°
∴BD= AD=4
在Rt△ABD中
,根据勾股定理
在Rt△ABC中,
又AD=8
A
B
C
D
30°
8
6、 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD
A
B
C
D
证明:
过A作AE⊥BC于E
E
∵AB=AC,∴BE=CE
在Rt △ADE中,
AD2=AE2+DE2
在Rt △ABE中,
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD
