勾股定理复习[下学期]
图片预览









文档简介
课件31张PPT。 八年级数学(下册)? 人教版
初二数学教研组第 十八 章
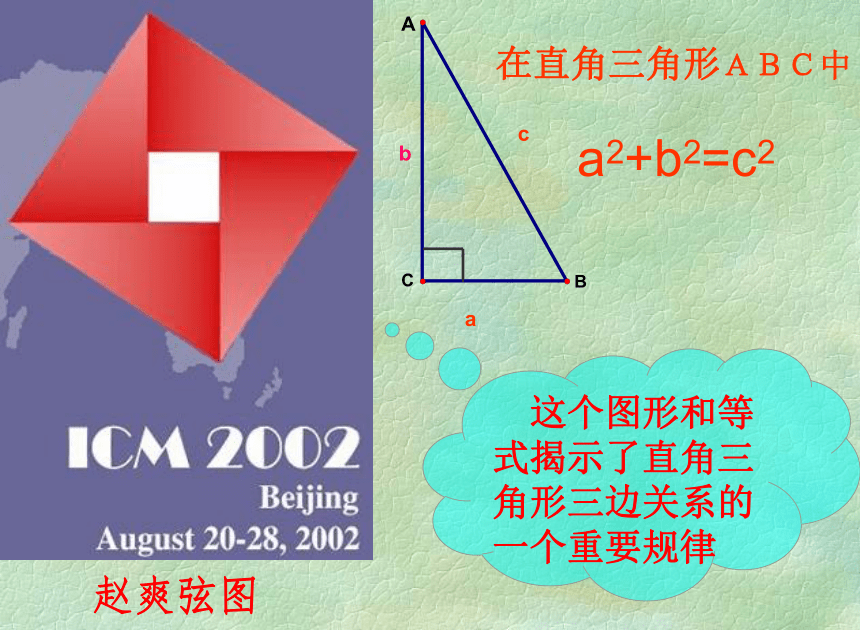
勾股定理的复习 如果直角三角形的两条直角边长分别为a、b,斜边为c,那么 a2 + b2 = c2 直角三角形两直角边的平方和等于斜边的平方。 注意:勾股定理只适用在直角三角形中求边之间的关系!勾股定理什么叫勾股定理?赵爽弦图 这个图形和等式揭示了直角三角形三边关系的一个重要规律
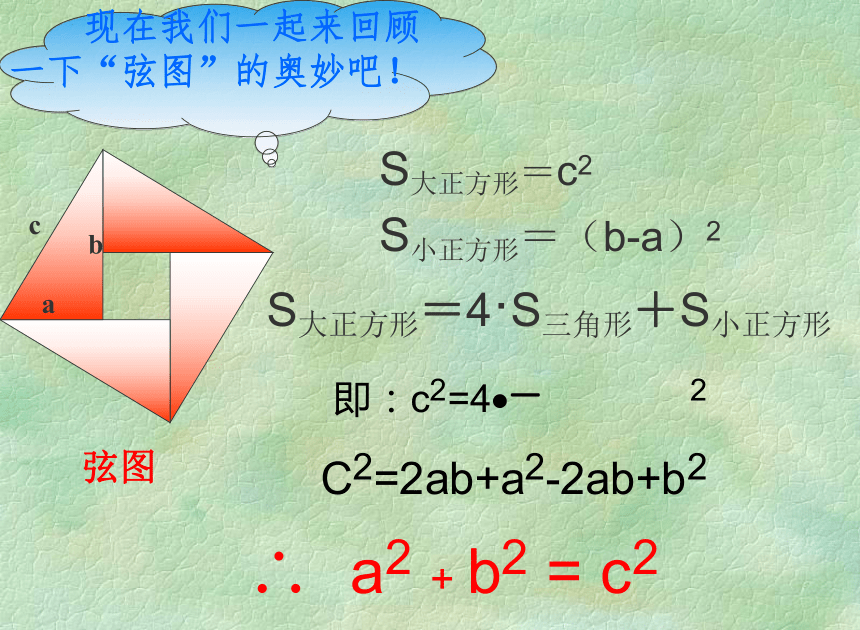
a2+b2=c2abc在直角三角形ABC中赵爽弦图它标志着我国古代数学的伟大成就!abcS大正方形=c2S小正方形=(b-a)2S大正方形=4·S三角形+S小正方形弦图 现在我们一起来回顾一下“弦图”的奥妙吧!用面积法证明等式是数学中常用的方法
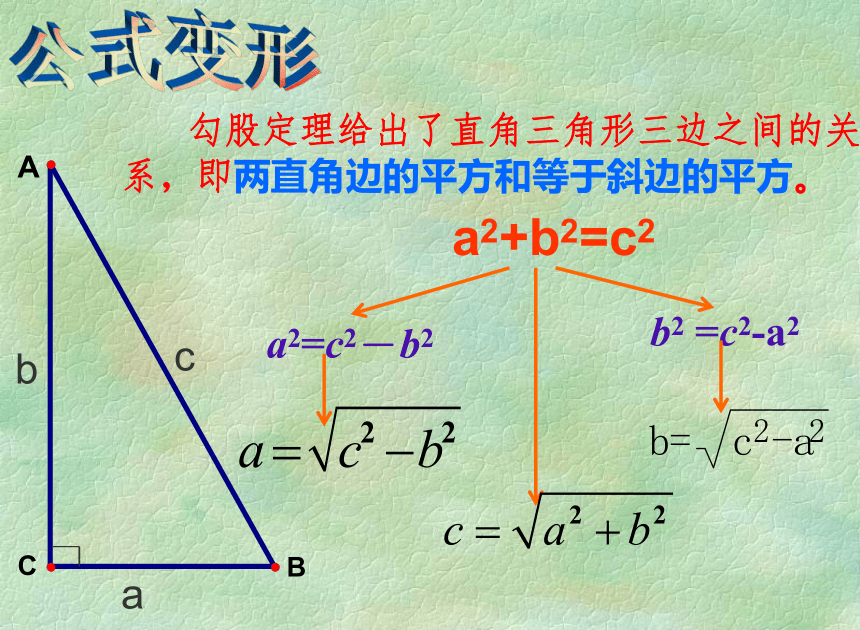
它是数形结合的数学思想的精巧展现方法与思想 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形a2=c2-b2b2 =c2-a2a2+b2=c2
比一比,看谁快!在Rt△ABC中,∠C=900
①若a=6,b=8, 则c=___;
②若a=40,c=41,则b=____;
③若a:b=1:2,c= 2 则S△ABC=____;
④若∠A=30°,a=2,则c=____,b=___,
a:b:c=_______;
⑤若∠A= ∠C,c= ,
则a=___,a:b:c=________.109414勾股定理的运用想一想:例1 印度有一数学家婆什迦罗曾提出过“荷花问题”:“平平湖水清可鉴, 面上半尺生红莲;
出泥不染亭亭立, 忽被强风吹水面。
渔人观看忙向前, 花离原位二尺远;
能算诸君请解题, 湖水如何知深浅?”“平平湖水清可鉴, 面上半尺生红莲; 出泥不染亭亭立, 忽被强风吹水面。
渔人观看忙向前, 花离原位二尺远;能算诸君请解题, 湖水如何知深浅?”分析:先把实际问题转化成
数学问题。求:AB的长。已知:AD = 0.5 尺, AC = 2尺,
且∠CAB = 90o,BD =BC根据勾股定理得: 解得 x = 3.75 (尺)答:湖水深3.75尺。解:设AB= x,则BD = x + 0.5,所以BC = BD = x + 0.5,在Rt△ABC中,∠BAC = 90o ,所以有:( x + 0.5 )2 = x2 + 22求:AB的长。已知:AD = 0.5 尺, AC = 2尺,
且∠CAB = 90o,BD = BC你能利用勾股定理设计一个测量学校旗杆高度的方案吗?想一想mnxX+m解:设旗杆高为x米,则绳长为(x+m)米在直角三角形中,有
X2+n2=(x+m)2
解得:x=(n2-m2)/2m你能用其它方法
测量吗? 试一试
将长为10米的梯子AC斜靠在墙上,BC长为6米.
(1)梯子上端A下滑2米后,底端将
水平滑动2米吗?
(2)换个下滑的数据算算,你能得
到什么结论?ACBA1C1例2、如图,点A是一个半径为 250 m的圆形森林公园的中心,在森林公园附近有 B .C 两个小镇,现要在 B.C 两小镇之间修一条长为 1000 m 的笔直公路将两镇连通,经测得 ∠B=60°,∠C=30°,问?请通过计算说明此公路会不会穿过该森林公园.250100060°30°D解:在△ABC中∠B=60°,∠C=30°,
∴∠BAC=900
∴在Rt△ABC中,AB= BC=500
AC= =500
∵2S△ABC=AD×BC=AB×AC
∴AD=250 >250
∴此公路不会穿过该森林公园例3 如图,将长方形ABCD沿着BD所在直线折叠,
BC交AD于点E,
(1)求证:△EBD是等腰三角形
(2)当AD=8,AB=4时,求△EBD的面积AECBD试一试如图,有一张直角三角形纸片,两
直角边长AC=6cm,BC=8cm,现将直角边
AC沿直线AD折叠,使它落在斜边AB上,且
与AE重合,则CD等于( )
A 2cm B 3cm C 4cm D 5cmBECADB68XX61048-X(8-X)2=X2+42解得:X=3 总结规律:
1、关于折叠问题,能得到:
(1)相等的线段,相等的角;
(2)全等三角形。
2、解这类题通常将一些未知的、
已知的元素挤入一个三角形中。 如果三角形的三边长边长a、b,c,
满足 a2 + b2 = c2 ,
那么这个三角形是直角三角形 根据三角形三边关系判断三角形的形状勾股定理的逆定理 赛一赛,看谁准 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ;(5)a=2m b=m2-1 c=m2+1是∠ C=900勾股定理逆定理的运用 ⒉ 小明向东走80m后,又走了60m,再走100m
回到原地,小明向东走80m后,又向
方向走的.南或北例4、△ABC中,AB=13cm,BC=10cm,
BC边上的中线AD=12cm,
试判断△ABC的形状解:∵AD是BC边上的中线,BC=10
∴BD=CD=5
在△ABD中,BD=5,AD=12,
AB=13
∴BD2+AD2=AB2
∴∠ADB= ∠ADC=90 °
∴AC2=CD2+AD2=169,
∴AC=13=AB
∴ △ABC是等腰三角形
勾股定理和它的逆定理的综合运用例5 一个零件的形状如图,量得一个零件的尺寸下:
AB=3cm ,AD=4cm,BC=13cm,CD=12cm
且∠DAB=90°,你能求这个零件的面积吗?3413125解:在Rt△ABC中,AB=3,AD=4∴DB= = 5
在△BCD中,DB2+DC2=169
BC2=169
∴DB2+DC2=BC2
∴∠BDC=900
S=S△ABD=S△BCD= ×3×4
+ ×12×5=36
答:这个零件的面积为36cm2有一块菜地,形状如下,
试求它的面积.(单位:米)试一试例6、如图,在正方形ABDC中,E是CD的中点,F为BD上一点,且BF=3FD, 试猜想线段AE,EF的位置关系并证明.解: ∠AEF=900
设FD=1则BF=3,BD=AB=
AC=CD=4 DE=CE=2
在Rt△ABF中,AF2=AB2+BP2=25
在Rt △ DEF中,EF2=DF2+DE2=5
在Rt △ AEC,AE2=AC2+EC2=20
∴EF2+AE2=AF2
∴∠AEF=900考考你! 你能分别在下列正方形中画出格点三角形,使它是直角三角形,且各顶点在正方形的三条边上(没有两点在正方形的同一边上).并能给予说明吗? 今日事 今日毕?我最大的收获是……??
课堂聚焦 今日事 今日毕作业:作业:
(1) 复习课本 P72~89
(2) P79 9 10 11 12
P88 5 6 7 8 9 再 见
初二数学教研组第 十八 章
勾股定理的复习 如果直角三角形的两条直角边长分别为a、b,斜边为c,那么 a2 + b2 = c2 直角三角形两直角边的平方和等于斜边的平方。 注意:勾股定理只适用在直角三角形中求边之间的关系!勾股定理什么叫勾股定理?赵爽弦图 这个图形和等式揭示了直角三角形三边关系的一个重要规律
a2+b2=c2abc在直角三角形ABC中赵爽弦图它标志着我国古代数学的伟大成就!abcS大正方形=c2S小正方形=(b-a)2S大正方形=4·S三角形+S小正方形弦图 现在我们一起来回顾一下“弦图”的奥妙吧!用面积法证明等式是数学中常用的方法
它是数形结合的数学思想的精巧展现方法与思想 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形a2=c2-b2b2 =c2-a2a2+b2=c2
比一比,看谁快!在Rt△ABC中,∠C=900
①若a=6,b=8, 则c=___;
②若a=40,c=41,则b=____;
③若a:b=1:2,c= 2 则S△ABC=____;
④若∠A=30°,a=2,则c=____,b=___,
a:b:c=_______;
⑤若∠A= ∠C,c= ,
则a=___,a:b:c=________.109414勾股定理的运用想一想:例1 印度有一数学家婆什迦罗曾提出过“荷花问题”:“平平湖水清可鉴, 面上半尺生红莲;
出泥不染亭亭立, 忽被强风吹水面。
渔人观看忙向前, 花离原位二尺远;
能算诸君请解题, 湖水如何知深浅?”“平平湖水清可鉴, 面上半尺生红莲; 出泥不染亭亭立, 忽被强风吹水面。
渔人观看忙向前, 花离原位二尺远;能算诸君请解题, 湖水如何知深浅?”分析:先把实际问题转化成
数学问题。求:AB的长。已知:AD = 0.5 尺, AC = 2尺,
且∠CAB = 90o,BD =BC根据勾股定理得: 解得 x = 3.75 (尺)答:湖水深3.75尺。解:设AB= x,则BD = x + 0.5,所以BC = BD = x + 0.5,在Rt△ABC中,∠BAC = 90o ,所以有:( x + 0.5 )2 = x2 + 22求:AB的长。已知:AD = 0.5 尺, AC = 2尺,
且∠CAB = 90o,BD = BC你能利用勾股定理设计一个测量学校旗杆高度的方案吗?想一想mnxX+m解:设旗杆高为x米,则绳长为(x+m)米在直角三角形中,有
X2+n2=(x+m)2
解得:x=(n2-m2)/2m你能用其它方法
测量吗? 试一试
将长为10米的梯子AC斜靠在墙上,BC长为6米.
(1)梯子上端A下滑2米后,底端将
水平滑动2米吗?
(2)换个下滑的数据算算,你能得
到什么结论?ACBA1C1例2、如图,点A是一个半径为 250 m的圆形森林公园的中心,在森林公园附近有 B .C 两个小镇,现要在 B.C 两小镇之间修一条长为 1000 m 的笔直公路将两镇连通,经测得 ∠B=60°,∠C=30°,问?请通过计算说明此公路会不会穿过该森林公园.250100060°30°D解:在△ABC中∠B=60°,∠C=30°,
∴∠BAC=900
∴在Rt△ABC中,AB= BC=500
AC= =500
∵2S△ABC=AD×BC=AB×AC
∴AD=250 >250
∴此公路不会穿过该森林公园例3 如图,将长方形ABCD沿着BD所在直线折叠,
BC交AD于点E,
(1)求证:△EBD是等腰三角形
(2)当AD=8,AB=4时,求△EBD的面积AECBD试一试如图,有一张直角三角形纸片,两
直角边长AC=6cm,BC=8cm,现将直角边
AC沿直线AD折叠,使它落在斜边AB上,且
与AE重合,则CD等于( )
A 2cm B 3cm C 4cm D 5cmBECADB68XX61048-X(8-X)2=X2+42解得:X=3 总结规律:
1、关于折叠问题,能得到:
(1)相等的线段,相等的角;
(2)全等三角形。
2、解这类题通常将一些未知的、
已知的元素挤入一个三角形中。 如果三角形的三边长边长a、b,c,
满足 a2 + b2 = c2 ,
那么这个三角形是直角三角形 根据三角形三边关系判断三角形的形状勾股定理的逆定理 赛一赛,看谁准 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ;(5)a=2m b=m2-1 c=m2+1是∠ C=900勾股定理逆定理的运用 ⒉ 小明向东走80m后,又走了60m,再走100m
回到原地,小明向东走80m后,又向
方向走的.南或北例4、△ABC中,AB=13cm,BC=10cm,
BC边上的中线AD=12cm,
试判断△ABC的形状解:∵AD是BC边上的中线,BC=10
∴BD=CD=5
在△ABD中,BD=5,AD=12,
AB=13
∴BD2+AD2=AB2
∴∠ADB= ∠ADC=90 °
∴AC2=CD2+AD2=169,
∴AC=13=AB
∴ △ABC是等腰三角形
勾股定理和它的逆定理的综合运用例5 一个零件的形状如图,量得一个零件的尺寸下:
AB=3cm ,AD=4cm,BC=13cm,CD=12cm
且∠DAB=90°,你能求这个零件的面积吗?3413125解:在Rt△ABC中,AB=3,AD=4∴DB= = 5
在△BCD中,DB2+DC2=169
BC2=169
∴DB2+DC2=BC2
∴∠BDC=900
S=S△ABD=S△BCD= ×3×4
+ ×12×5=36
答:这个零件的面积为36cm2有一块菜地,形状如下,
试求它的面积.(单位:米)试一试例6、如图,在正方形ABDC中,E是CD的中点,F为BD上一点,且BF=3FD, 试猜想线段AE,EF的位置关系并证明.解: ∠AEF=900
设FD=1则BF=3,BD=AB=
AC=CD=4 DE=CE=2
在Rt△ABF中,AF2=AB2+BP2=25
在Rt △ DEF中,EF2=DF2+DE2=5
在Rt △ AEC,AE2=AC2+EC2=20
∴EF2+AE2=AF2
∴∠AEF=900考考你! 你能分别在下列正方形中画出格点三角形,使它是直角三角形,且各顶点在正方形的三条边上(没有两点在正方形的同一边上).并能给予说明吗? 今日事 今日毕?我最大的收获是……??
课堂聚焦 今日事 今日毕作业:作业:
(1) 复习课本 P72~89
(2) P79 9 10 11 12
P88 5 6 7 8 9 再 见
