第18章勾股定理总复习[下学期]
文档属性
| 名称 | 第18章勾股定理总复习[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 536.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-06-12 00:00:00 | ||
图片预览









文档简介
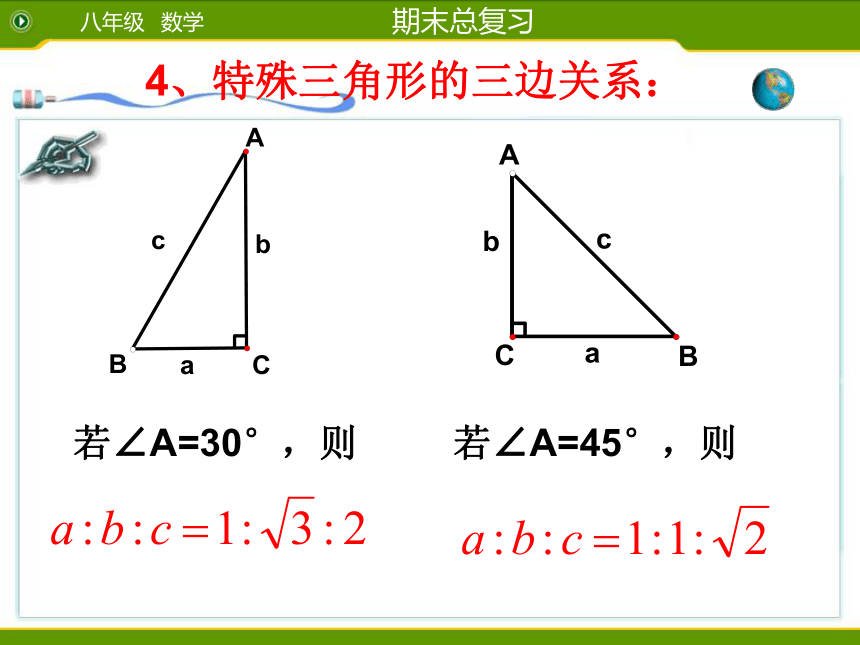
课件38张PPT。八年级第18章勾股定理直角三角形两直角边的平方和等于斜边的平方。 1、勾股定理知识回顾2、勾股定理的逆定理那么这个三角形是直角三角形.如果三角形的三边长a,b,c满足:3、常用的勾股数:3、4、5;5、12、13;7、24、25;8、15、17;9、40、41.4、特殊三角形的三边关系:若∠A=30°,则若∠A=45°,则6、命题与逆命题有何关系?什么是互逆定理?5、直角三角形中的有关定理(1)在直角三角形中,30°角所对的直角边等于斜边的一半。(2)在直角三角形中,一条直角边等于斜边的一半,则这条直角边所对的角为30°。(3)直角三角形斜边上的中线等于斜边的一半。数学思想方法(1)用面积法证明等式是数学中常用的方法(2)勾股定理和逆定理是数形结合的数学思想的精巧展现2、分类讨论思想;4、转化思想;3、数形结合思想;1、方程思想;abcS大正方形=c2S小正方形=(b-a)2S大正方形=4·S三角形+S小正方形 现在我们一起来回顾一下“赵爽弦图”的奥妙吧!赵爽弦图疑点点拨1、“所有的命题都有逆命题,所有的定理都有逆定理”这种说法对吗?3、在△ABC中,AC=6,BC=8,则AB的长为( )
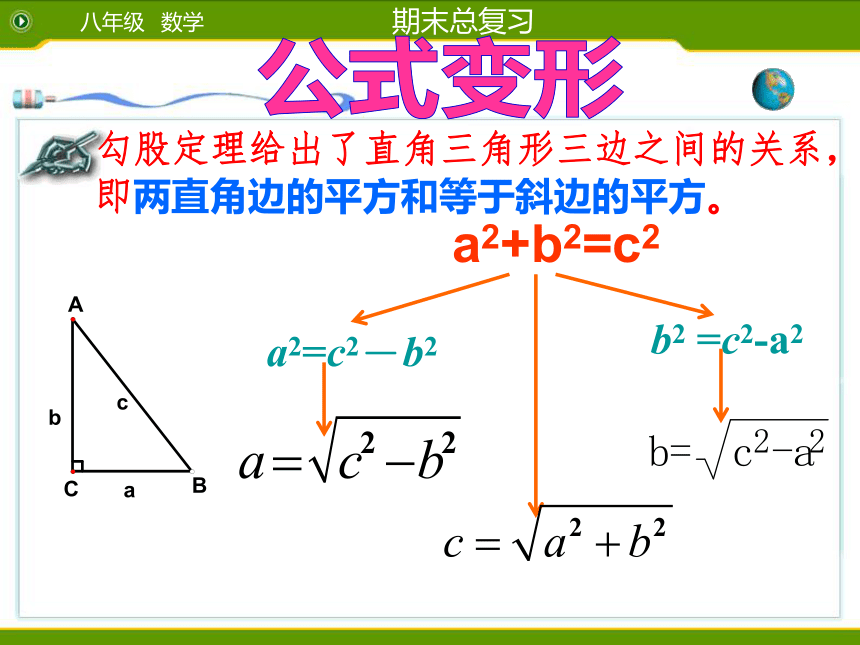
(A)10 (B)2 (C)4 (D)无法确定4、已知直角三角形的两边长分别为3、4,则第三边长为 。5、以线段a=0.6,b=1,C=0.8为边组成的三角形是不是直角三角形?2、命题“直角三角形中30°角所对的直角边等于斜边的一半”的逆命题是 。 考点一与勾股定理有关的计算问题考点例析勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。公式变形a2=c2-b2b2 =c2-a2a2+b2=c2
④若∠A=30°,a=2,则c=____,b=___,
a:b:c=_______;比一比,看谁快!1、在Rt△ABC中,∠C=900
①若a=6,b=8, 则c=___;⑤若∠A= ∠C,c= ,
则a=___,a:b:c=________.10941③若a:b=1:2,c= 2 则S△ABC=____;4②若a=40,c=41,则b=____;2、已知Rt△ABC中,∠C=90°,若a+b=14cm,
c=10cm,则Rt△ABC的面积是( )
A、24cm2 B、36cm2 C、48cm2 D、60cm23、直角三角形有一条直角边的长为11,另外两边的长也是正整数,则此三角形的周长是( )
A、120 B、121 C、132 D、1234、已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。
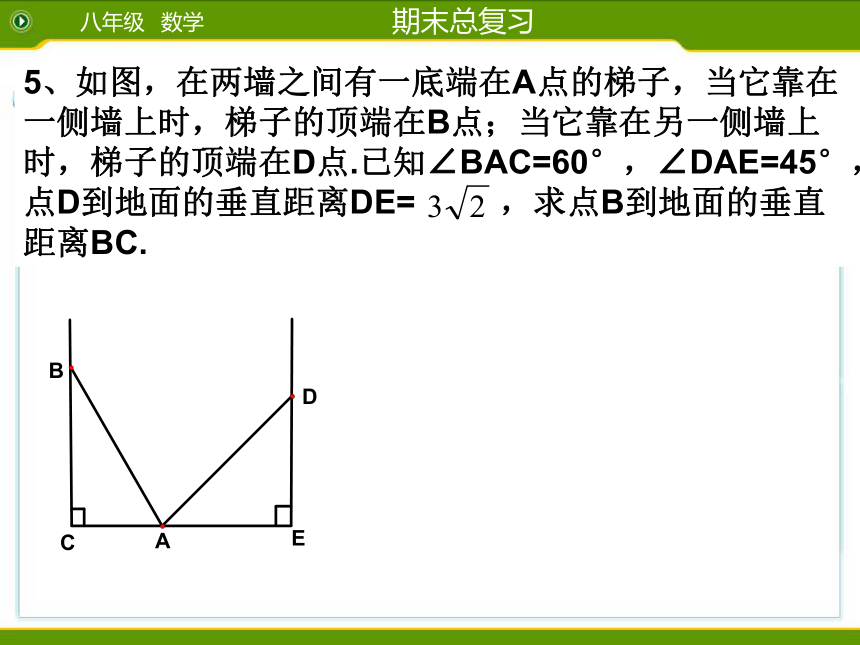
求:四边形ABCD的面积。 5、如图,在两墙之间有一底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE= ,求点B到地面的垂直距离BC.6、已知,如图,在Rt△ABC中,∠C=90°,
∠1=∠2,CD=1.5, BD=2.5, 求AC的长.提示:作辅助线DE⊥AB,利用平分线的性质和勾股定理。7、等腰三角形底边上的高为8,周长为32,求这个三角形的面积8DABC解:设这个三角形为ABC,高为AD,设BD为x,则AB为(16-x), 由勾股定理得:
x2+82=(16-x)2即x2+64=256-32x+x2∴ x=6∴ S?ABC=BC?AD/2=2 ?6 ?8/2=488、在△ABC中,∠BAC=120°,AB=AC= cm,一动点P从B向C以每秒2cm的速度移动,问当P点移动多少秒时,PA与腰垂直。 9、已知:如图,在△ABC中,∠C=60°,AB= ,AC=4,AD是BC边上的高,求BC的长。 10、将长为10米的梯子AC斜靠在墙上,BC长为6米.
(1)梯子上端A下滑2米后,底端将水平滑动2米吗?
(2)换个下滑的数据算算,你能得到什么结论?ACBA1C1考点二 与展开图形有关的计算问题1、如图,所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图(2)所示.已知展开图中每个正方形的边长为1.
(1)求在该展开图中可画出最长线段的长度?这样的线段可画几条?
(2)试比较立体图中∠BAC与平面展开图中∠B/A/C/的大小关系?2、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.考点三与勾股定理有关的证明题1、△ABC中,BC=a,AC=b,AB=c.若∠C=90°,如图l,根据勾股定理,则a2+b2=c2。若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.2、已知,△ABC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,试说明△ABC是等腰三角形。提示: 先运用勾股定理证明中线AD⊥BC,再利用等腰三角形的判定方法就可以说明了. 3、如图,在△ABC中,AB=AC,P为BC上任意一点,证明:AB2-AP2=PB×PC。解:过A点作AD⊥BCD在 Rt△ABD中,根据勾股定理,得:
AB2=AD2+BD2 ①
同理: AP2=AD2+DP2 ②
由①-②,得
AB2-AP2=BD2-DP2
=(BD+DP)(BD-DP)
=PB(BD+DP)
又 AB=AC, AD⊥BC ∴ BD=CD
∴ AB2-AP2=PB×PC4、如图,有一张直角三角形纸片,两直角边长AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
A 2cm B 3cm C 4cm D 5cmBECADB68xx61048-x(8-x)2=x2+42解得:x=3 5、 如图,将长方形ABCD沿着BD所在直线折叠,
BC交AD于点E,
(1)求证:△EBD是等腰三角形
(2)当AD=8,AB=4时,求△EBD的面积AECBD考点四勾股定理的实际应用分析:先把实际问题转化成数学问题。已知:AD = 0.5 尺, AC = 2尺,
且∠CAB = 90o, BD =BC,求:AB的长.1、 印度有一数学家婆什迦罗曾提出过“荷花问题”:“平平湖水清可鉴, 面上半尺生红莲;
出泥不染亭亭立, 忽被强风吹水面。
渔人观看忙向前, 花离原位二尺远;
能算诸君请解题, 湖水如何知深浅?”2、如图,点A是一个半径为 250 m的圆形森林公园的中心,在森林公园附近有 B .C 两个小镇,现要在 B.C 两小镇之间修一条长为 1000 m 的笔直公路将两镇连通,经测得 ∠B=60°,∠C=30°,问?请通过计算说明此公路会不会穿过该森林公园.250100060°30°D解:在△ABC中∠B=60°,∠C=30°,
∴∠BAC=900
∴在Rt△ABC中,AB= BC=500
AC= =500
∵2S△ABC=AD×BC=AB×AC
∴AD=250 >250
∴此公路不会穿过该森林公园考点五勾股定理逆定理的应用 赛一赛,看谁准 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ;(5)a=2m b=m2-1 c=m2+1是∠ C=900 2、小明向东走80m后,又走了60m,再走100m回到原地,小明向东走80m后,又向 方向走的.南或北3、△ABC中,AB=13cm,BC=10cm,BC边上的中线AD=12cm, 试判断△ABC的形状解:∵AD是BC边上的中线,BC=10
∴BD=CD=5
在△ABD中,BD=5,AD=12,
AB=13
∴BD2+AD2=AB2
∴∠ADB= ∠ADC=90 °
∴AC2=CD2+AD2=169,
∴AC=13=AB
∴ △ABC是等腰三角形4、 一个零件的形状如图,量得一个零件的尺寸下:
AB=3cm ,AD=4cm,BC=13cm,CD=12cm
且∠DAB=90°,你能求这个零件的面积吗?3413125解:在Rt△ABC中,AB=3,AD=4∴DB= = 5
在△BCD中,DB2+DC2=169
BC2=169
∴DB2+DC2=BC2
∴∠BDC=900
S=S△ABD=S△BCD= ×3×4
+ ×12×5=36
答:这个零件的面积为36cm25、有一块菜地,形状如下, 试求它的面积.(单位:米)6、如图,在正方形ABDC中,E是CD的中点,F为BD上一点,且BF=3FD,试猜想线段AE,EF的位置关系并证明.解: ∠AEF=900
设FD=1则BF=3,BD=AB=
AC=CD=4 DE=CE=2
在Rt△ABF中,AF2=AB2+BP2=25
在Rt △ DEF中,EF2=DF2+DE2=5
在Rt △ AEC,AE2=AC2+EC2=20
∴EF2+AE2=AF2
∴∠AEF=9001、你能分别在下列正方形中画出格点三角形,使它是直角三角形,且各顶点在正方形的三条边上(没有两点在正方形的同一边上).并能给予说明吗?2、下列图①、②、③中的阴影部分分别是以直角三角形的三边为边长所作的正多边形;图④中的阴影部分分别是以直角三角形的三边为直径所作的半圆。根据勾股定理可知:分别以直角三角形的两条直角边为边长的正方形面积之和等于以斜边为边长的正方形的面积(如图②)
(1)类似的结论,对于图②的结论,对于图①、③、④是否成立?如果成立,请选择其中一个图形进行证明。
(2)根据(1)的结论,你能提出一般性的结论吗?写出你的结论并给予证明。 感悟与收获今日事 今日毕?我最大的收获是……?
(A)10 (B)2 (C)4 (D)无法确定4、已知直角三角形的两边长分别为3、4,则第三边长为 。5、以线段a=0.6,b=1,C=0.8为边组成的三角形是不是直角三角形?2、命题“直角三角形中30°角所对的直角边等于斜边的一半”的逆命题是 。 考点一与勾股定理有关的计算问题考点例析勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。公式变形a2=c2-b2b2 =c2-a2a2+b2=c2
④若∠A=30°,a=2,则c=____,b=___,
a:b:c=_______;比一比,看谁快!1、在Rt△ABC中,∠C=900
①若a=6,b=8, 则c=___;⑤若∠A= ∠C,c= ,
则a=___,a:b:c=________.10941③若a:b=1:2,c= 2 则S△ABC=____;4②若a=40,c=41,则b=____;2、已知Rt△ABC中,∠C=90°,若a+b=14cm,
c=10cm,则Rt△ABC的面积是( )
A、24cm2 B、36cm2 C、48cm2 D、60cm23、直角三角形有一条直角边的长为11,另外两边的长也是正整数,则此三角形的周长是( )
A、120 B、121 C、132 D、1234、已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。
求:四边形ABCD的面积。 5、如图,在两墙之间有一底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE= ,求点B到地面的垂直距离BC.6、已知,如图,在Rt△ABC中,∠C=90°,
∠1=∠2,CD=1.5, BD=2.5, 求AC的长.提示:作辅助线DE⊥AB,利用平分线的性质和勾股定理。7、等腰三角形底边上的高为8,周长为32,求这个三角形的面积8DABC解:设这个三角形为ABC,高为AD,设BD为x,则AB为(16-x), 由勾股定理得:
x2+82=(16-x)2即x2+64=256-32x+x2∴ x=6∴ S?ABC=BC?AD/2=2 ?6 ?8/2=488、在△ABC中,∠BAC=120°,AB=AC= cm,一动点P从B向C以每秒2cm的速度移动,问当P点移动多少秒时,PA与腰垂直。 9、已知:如图,在△ABC中,∠C=60°,AB= ,AC=4,AD是BC边上的高,求BC的长。 10、将长为10米的梯子AC斜靠在墙上,BC长为6米.
(1)梯子上端A下滑2米后,底端将水平滑动2米吗?
(2)换个下滑的数据算算,你能得到什么结论?ACBA1C1考点二 与展开图形有关的计算问题1、如图,所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图(2)所示.已知展开图中每个正方形的边长为1.
(1)求在该展开图中可画出最长线段的长度?这样的线段可画几条?
(2)试比较立体图中∠BAC与平面展开图中∠B/A/C/的大小关系?2、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.考点三与勾股定理有关的证明题1、△ABC中,BC=a,AC=b,AB=c.若∠C=90°,如图l,根据勾股定理,则a2+b2=c2。若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.2、已知,△ABC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,试说明△ABC是等腰三角形。提示: 先运用勾股定理证明中线AD⊥BC,再利用等腰三角形的判定方法就可以说明了. 3、如图,在△ABC中,AB=AC,P为BC上任意一点,证明:AB2-AP2=PB×PC。解:过A点作AD⊥BCD在 Rt△ABD中,根据勾股定理,得:
AB2=AD2+BD2 ①
同理: AP2=AD2+DP2 ②
由①-②,得
AB2-AP2=BD2-DP2
=(BD+DP)(BD-DP)
=PB(BD+DP)
又 AB=AC, AD⊥BC ∴ BD=CD
∴ AB2-AP2=PB×PC4、如图,有一张直角三角形纸片,两直角边长AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
A 2cm B 3cm C 4cm D 5cmBECADB68xx61048-x(8-x)2=x2+42解得:x=3 5、 如图,将长方形ABCD沿着BD所在直线折叠,
BC交AD于点E,
(1)求证:△EBD是等腰三角形
(2)当AD=8,AB=4时,求△EBD的面积AECBD考点四勾股定理的实际应用分析:先把实际问题转化成数学问题。已知:AD = 0.5 尺, AC = 2尺,
且∠CAB = 90o, BD =BC,求:AB的长.1、 印度有一数学家婆什迦罗曾提出过“荷花问题”:“平平湖水清可鉴, 面上半尺生红莲;
出泥不染亭亭立, 忽被强风吹水面。
渔人观看忙向前, 花离原位二尺远;
能算诸君请解题, 湖水如何知深浅?”2、如图,点A是一个半径为 250 m的圆形森林公园的中心,在森林公园附近有 B .C 两个小镇,现要在 B.C 两小镇之间修一条长为 1000 m 的笔直公路将两镇连通,经测得 ∠B=60°,∠C=30°,问?请通过计算说明此公路会不会穿过该森林公园.250100060°30°D解:在△ABC中∠B=60°,∠C=30°,
∴∠BAC=900
∴在Rt△ABC中,AB= BC=500
AC= =500
∵2S△ABC=AD×BC=AB×AC
∴AD=250 >250
∴此公路不会穿过该森林公园考点五勾股定理逆定理的应用 赛一赛,看谁准 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ;(5)a=2m b=m2-1 c=m2+1是∠ C=900 2、小明向东走80m后,又走了60m,再走100m回到原地,小明向东走80m后,又向 方向走的.南或北3、△ABC中,AB=13cm,BC=10cm,BC边上的中线AD=12cm, 试判断△ABC的形状解:∵AD是BC边上的中线,BC=10
∴BD=CD=5
在△ABD中,BD=5,AD=12,
AB=13
∴BD2+AD2=AB2
∴∠ADB= ∠ADC=90 °
∴AC2=CD2+AD2=169,
∴AC=13=AB
∴ △ABC是等腰三角形4、 一个零件的形状如图,量得一个零件的尺寸下:
AB=3cm ,AD=4cm,BC=13cm,CD=12cm
且∠DAB=90°,你能求这个零件的面积吗?3413125解:在Rt△ABC中,AB=3,AD=4∴DB= = 5
在△BCD中,DB2+DC2=169
BC2=169
∴DB2+DC2=BC2
∴∠BDC=900
S=S△ABD=S△BCD= ×3×4
+ ×12×5=36
答:这个零件的面积为36cm25、有一块菜地,形状如下, 试求它的面积.(单位:米)6、如图,在正方形ABDC中,E是CD的中点,F为BD上一点,且BF=3FD,试猜想线段AE,EF的位置关系并证明.解: ∠AEF=900
设FD=1则BF=3,BD=AB=
AC=CD=4 DE=CE=2
在Rt△ABF中,AF2=AB2+BP2=25
在Rt △ DEF中,EF2=DF2+DE2=5
在Rt △ AEC,AE2=AC2+EC2=20
∴EF2+AE2=AF2
∴∠AEF=9001、你能分别在下列正方形中画出格点三角形,使它是直角三角形,且各顶点在正方形的三条边上(没有两点在正方形的同一边上).并能给予说明吗?2、下列图①、②、③中的阴影部分分别是以直角三角形的三边为边长所作的正多边形;图④中的阴影部分分别是以直角三角形的三边为直径所作的半圆。根据勾股定理可知:分别以直角三角形的两条直角边为边长的正方形面积之和等于以斜边为边长的正方形的面积(如图②)
(1)类似的结论,对于图②的结论,对于图①、③、④是否成立?如果成立,请选择其中一个图形进行证明。
(2)根据(1)的结论,你能提出一般性的结论吗?写出你的结论并给予证明。 感悟与收获今日事 今日毕?我最大的收获是……?
