勾股定理的复习(二节课内容)[下学期]
文档属性
| 名称 | 勾股定理的复习(二节课内容)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-06-20 00:00:00 | ||
图片预览








文档简介
课件30张PPT。勾股定理复习(第一课时)一、知识要点如果直角三角形两直角边分别为a,b,斜边为c,
那么勾股定理a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方. 满足a2 +b2=c2的三个正整数,称为勾股数勾 股 数2.勾股定理的逆定理:
三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.要点1: 在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论是第二个命题的题设,那么这两个命题叫做互逆命题.如果把其中一个命题叫做原命题,那么另一命题就叫做它的逆命题. 要点2: 每一个命题都有逆命题,只要将原命题的题设改成结论,并将结论改成题设,便可得到原命题的逆命题.但是原命题正确,它的逆命题未必正确.例如真命题“对顶角相等”的逆命题为“相等的角是对顶角”,此命题就是一个假命题.三.逆命题.逆定理要点3:如果一个定理的逆命题也是定理,那么这两个定理叫做互逆定理,其中的一个定理叫做另一个定理的逆定理.命题“两直线平行,内错角相等”和它的逆命题“内错角相等,两直线平行”都是定理,因此它们就是互逆定理.(一)、填空题1、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;
④若a∶b=3∶4,c=10则SRt△ABC=________。 2、直角三角形两直角边长分别为5和12,则它
斜边上的高为__________。 1320112460/13考点一:直角三角形边长的有关计算3.已知直角三角形两边x、y的长满足
则第三边的长为 (二)、选择题1.已知一个Rt△的两边长分别为3和4,则第三
边长的平方是( )
A、25 B、14 C、7 D、7或25D
2.如果Rt△两直角边的比为5∶12,则斜边上的
高与斜边的比为( )
A、60∶13 B、5∶12
C、12∶13 D、60∶169D3.如果Rt△的两直角边长分别为n2-1,2n(n>1), 那么它的斜边长是( )
A、2n B、n+1 C、n2-1 D、n2+1
4.已知Rt△ABC中,∠C=90°,若a+b=14cm,
c=10cm,则Rt△ABC的面积是( )
A、24cm2 B、36cm2 C、48cm2 D、60cm2
5.等腰三角形底边上的高为8,周长为32,则三
角形的面积为( )
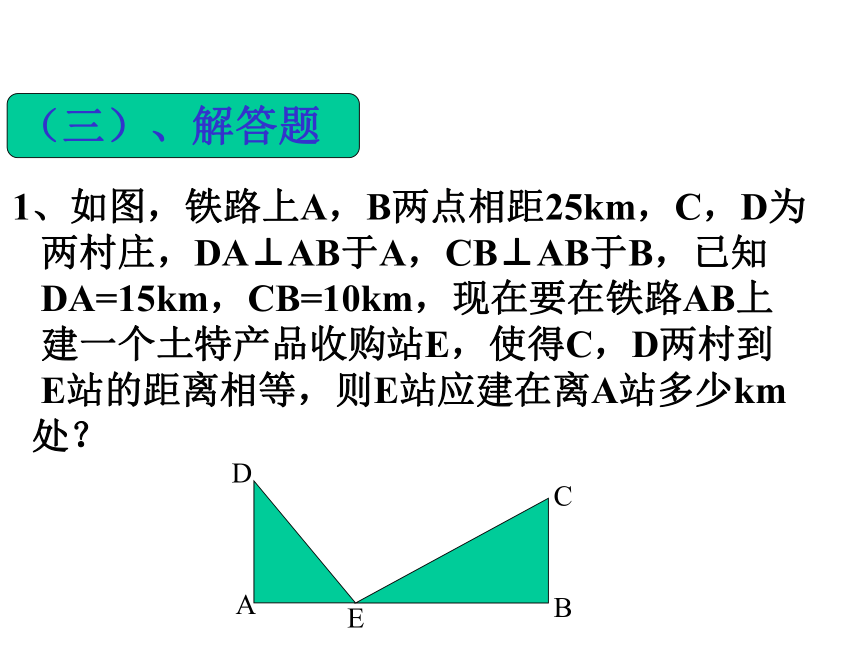
A、56 B、48 C、40 D、32DAB(三)、解答题1、如图,铁路上A,B两点相距25km,C,D为
两村庄,DA⊥AB于A,CB⊥AB于B,已知
DA=15km,CB=10km,现在要在铁路AB上
建一个土特产品收购站E,使得C,D两村到
E站的距离相等,则E站应建在离A站多少km
处?
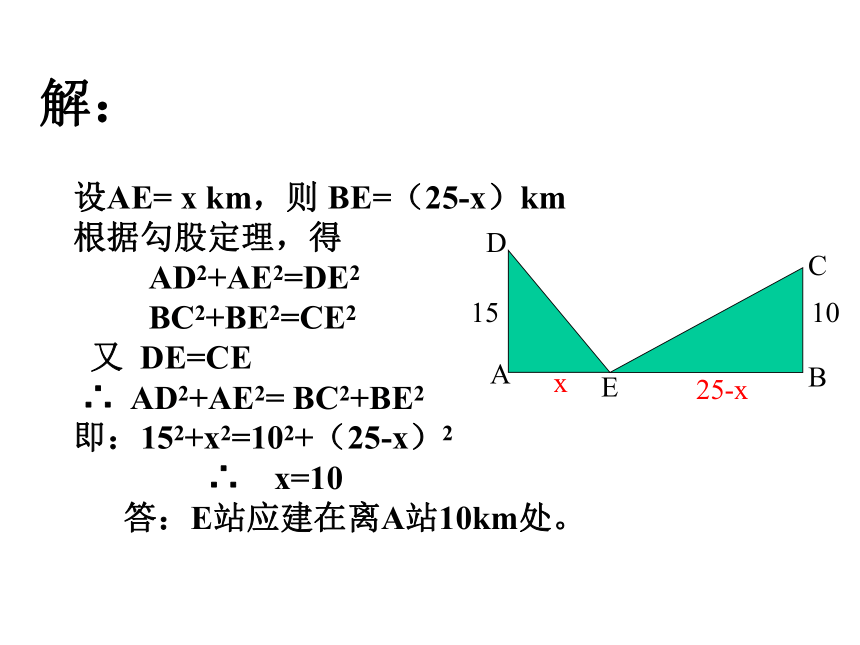
解:设AE= x km,则 BE=(25-x)km
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2
又 DE=CE
∴ AD2+AE2= BC2+BE2
即:152+x2=102+(25-x)2
∴ x=10
答:E站应建在离A站10km处。
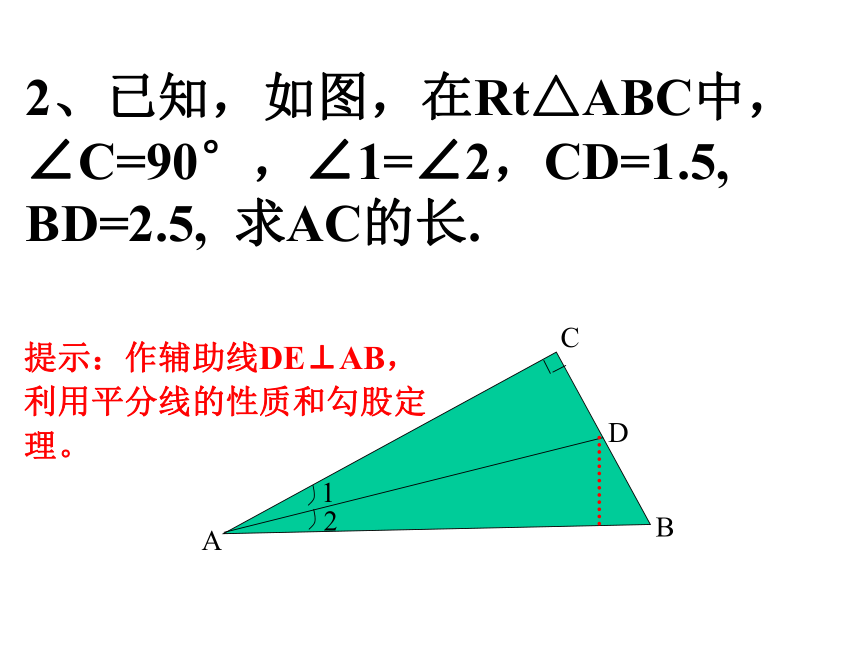
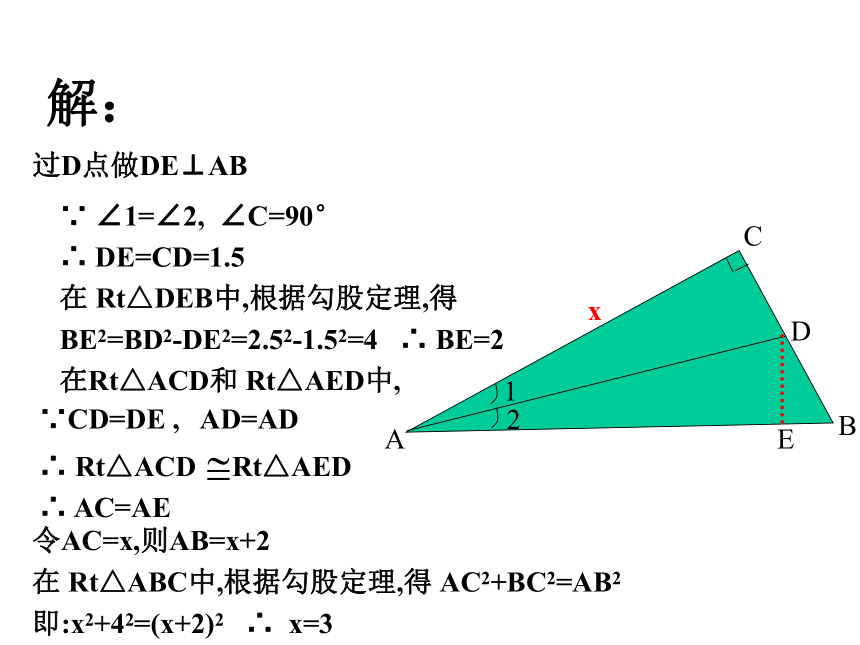
x25-x2、已知,如图,在Rt△ABC中,∠C=90°,∠1=∠2,CD=1.5, BD=2.5, 求AC的长.提示:作辅助线DE⊥AB,利用平分线的性质和勾股定理。解:过D点做DE⊥ABE∵ ∠1=∠2, ∠C=90°
∴ DE=CD=1.5
在 Rt△DEB中,根据勾股定理,得
BE2=BD2-DE2=2.52-1.52=4 ∴ BE=2
在Rt△ACD和 Rt△AED中,
∵CD=DE , AD=AD ∴ Rt△ACD Rt△AED
∴ AC=AE
令AC=x,则AB=x+2
在 Rt△ABC中,根据勾股定理,得 AC2+BC2=AB2
即:x2+42=(x+2)2 ∴ x=3x3.一个零件的形状如图所示,按规定这个零件中∠A与∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图所示,这个零件符合要求吗?求这个四边形的面积.ABCD43512134.如图,为测量小河的宽度,先在河边任取一点A,再在河的另一岸取两点B,C.测得∠ABC=450,∠ACB=300,量得BC长为10( +1)米,求小河的宽度.BCAD三、小结 本节课主要是应用勾股定理解决求三角形的边长问题,在应用定理时,应注意:1、没有图的要按题意画好图并标上字母;2、不要用错定理。1.如图所示,这是一块大家常用的一种橡皮,
如果AD=4厘米,CD=3厘米,BC=12厘米,
你能算出AB两点之间的距离吗?拓展题2、等腰三角形底边上的高为8,周长为32,求这个三角形的面积8DABC解:设这个三角形为ABC,高为AD,设BD为X,则AB为(16-X), 由勾股定理得:
X2+82=(16-X)2即X2+64=256-32X+X2∴ X=6∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48再见勾股定理复习(第二课时) 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形a2=c2-b2b2 =c2-a2a2+b2=c2
一. 赛一赛,看谁准 1.下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ;(5)a=2m b=m2-1 c=m2+1是∠ C=900考点二:勾股定理的逆定理应用 2.小明向东走80m后,又走了60m,再走100m回到原地,小明向东走80m后,又向 方向走的.南或北3.已知:数7和24,请你再写一个整数,
使这些数恰好是一个直角三角形三边的长,
则这个数可以是——254.命题“直角三角形中30°角所对的直角边等于斜边的一半”的逆命题是
。 直角三角形中,如果一条直角边等于斜边的一半,
那么这条直角边所对角等于300.2. 观察下列几组数据:(1) 8, 15, 17; (2) 7, 12, 15; (3)12, 15, 20; (4) 7, 24, 25. 其中能作为直角三角形三边长的有( )组
A. 1 B. 2 C. 3 D. 44、直角三角形有一条直角边的长为11,另外两边的长也是正整数,则此三角形的周长是( )
A、120 B、121 C、132 D、1231.下列各组数中,以a,b,c为边的三角形不是
Rt△的是( )
A、a=1.5,b=2,c=3 B、a=7,b=24,c=25
C、a=6,b=8,c=10 D、a=3,b=4,c=5(二)、选择题AB3.一个三角形的三边之比为3:4:5,则这个三角形三边上的高
之比为( )
A. 3:4:5 B. 5:4:3 C. 20:15:12 D. 10:8:3CC例1、△ABC中,AB=13cm,BC=10cm,
BC边上的中线AD=12cm,
试判断△ABC的形状解:∵AD是BC边上的中线,BC=10
∴BD=CD=5
在△ABD中,BD=5,AD=12,
AB=13
∴BD2+AD2=AB2
∴∠ADB= ∠ADC=90 °
∴AC2=CD2+AD2=169,
∴AC=13=AB
∴ △ABC是等腰三角形
考点三:运用勾股定理及逆定理证明与计算例2、如图,在正方形ABDC中,E是CD的中点,F为BD上一点,且BF=3FD,试猜想线段AE,EF的位置关系并证明.解: AE⊥EF
设FD=1则BF=3,BD=AB=
AC=CD=4 DE=CE=2
在Rt△ABF中,AF2=AB2+BF2=25
在Rt △ DEF中,EF2=DF2+DE2=5
在Rt △ AEC,AE2=AC2+EC2=20
∴EF2+AE2=AF2
∴∠AEF=900 , ∴AE⊥EF例3.下列图①、②、③中的阴影部分分别是以直角三角形的三边为边长所作的正多边形;图④中的阴影部分分别是以直角三角形的三边为直径所作的半圆。根据勾股定理可知:分别以直角三角形的两条直角边为边长的正方形面积之和等于以斜边为边长的正方形的面积(如图②)
(1)类似的结论,对于图②的结论,对于图①、③、④是否成立?如果成立,请选择其中一个图形进行证明。
(2)根据(1)的结论,你能提出一般性的结论吗?写出你的结论并给予证明。 思考题:
已知?ABC的三边a, b ,c满足:
a2+b2+c2+338=10a+24b+26c,
请你判断?ABC的形状, 并说明理由.考考你! 你能分别在下列正方形中画出格点三角形,使它是直角三角形,且各顶点在正方形的三条边上(没有两点在正方形的同一边上).并能给予说明吗?有一块菜地,形状如下,
试求它的面积.(单位:米)试一试8、在△ABC中,∠BAC=120°,AB=AC= cm,一动点P从B向C以每秒2cm的速度移动,问当P点移动多少秒时,PA与腰垂直。 9、已知:如图,在△ABC中,∠C=60°,AB= ,AC=4,AD是BC边上的高,求BC的长。
那么勾股定理a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方. 满足a2 +b2=c2的三个正整数,称为勾股数勾 股 数2.勾股定理的逆定理:
三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.要点1: 在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论是第二个命题的题设,那么这两个命题叫做互逆命题.如果把其中一个命题叫做原命题,那么另一命题就叫做它的逆命题. 要点2: 每一个命题都有逆命题,只要将原命题的题设改成结论,并将结论改成题设,便可得到原命题的逆命题.但是原命题正确,它的逆命题未必正确.例如真命题“对顶角相等”的逆命题为“相等的角是对顶角”,此命题就是一个假命题.三.逆命题.逆定理要点3:如果一个定理的逆命题也是定理,那么这两个定理叫做互逆定理,其中的一个定理叫做另一个定理的逆定理.命题“两直线平行,内错角相等”和它的逆命题“内错角相等,两直线平行”都是定理,因此它们就是互逆定理.(一)、填空题1、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;
④若a∶b=3∶4,c=10则SRt△ABC=________。 2、直角三角形两直角边长分别为5和12,则它
斜边上的高为__________。 1320112460/13考点一:直角三角形边长的有关计算3.已知直角三角形两边x、y的长满足
则第三边的长为 (二)、选择题1.已知一个Rt△的两边长分别为3和4,则第三
边长的平方是( )
A、25 B、14 C、7 D、7或25D
2.如果Rt△两直角边的比为5∶12,则斜边上的
高与斜边的比为( )
A、60∶13 B、5∶12
C、12∶13 D、60∶169D3.如果Rt△的两直角边长分别为n2-1,2n(n>1), 那么它的斜边长是( )
A、2n B、n+1 C、n2-1 D、n2+1
4.已知Rt△ABC中,∠C=90°,若a+b=14cm,
c=10cm,则Rt△ABC的面积是( )
A、24cm2 B、36cm2 C、48cm2 D、60cm2
5.等腰三角形底边上的高为8,周长为32,则三
角形的面积为( )
A、56 B、48 C、40 D、32DAB(三)、解答题1、如图,铁路上A,B两点相距25km,C,D为
两村庄,DA⊥AB于A,CB⊥AB于B,已知
DA=15km,CB=10km,现在要在铁路AB上
建一个土特产品收购站E,使得C,D两村到
E站的距离相等,则E站应建在离A站多少km
处?
解:设AE= x km,则 BE=(25-x)km
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2
又 DE=CE
∴ AD2+AE2= BC2+BE2
即:152+x2=102+(25-x)2
∴ x=10
答:E站应建在离A站10km处。
x25-x2、已知,如图,在Rt△ABC中,∠C=90°,∠1=∠2,CD=1.5, BD=2.5, 求AC的长.提示:作辅助线DE⊥AB,利用平分线的性质和勾股定理。解:过D点做DE⊥ABE∵ ∠1=∠2, ∠C=90°
∴ DE=CD=1.5
在 Rt△DEB中,根据勾股定理,得
BE2=BD2-DE2=2.52-1.52=4 ∴ BE=2
在Rt△ACD和 Rt△AED中,
∵CD=DE , AD=AD ∴ Rt△ACD Rt△AED
∴ AC=AE
令AC=x,则AB=x+2
在 Rt△ABC中,根据勾股定理,得 AC2+BC2=AB2
即:x2+42=(x+2)2 ∴ x=3x3.一个零件的形状如图所示,按规定这个零件中∠A与∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图所示,这个零件符合要求吗?求这个四边形的面积.ABCD43512134.如图,为测量小河的宽度,先在河边任取一点A,再在河的另一岸取两点B,C.测得∠ABC=450,∠ACB=300,量得BC长为10( +1)米,求小河的宽度.BCAD三、小结 本节课主要是应用勾股定理解决求三角形的边长问题,在应用定理时,应注意:1、没有图的要按题意画好图并标上字母;2、不要用错定理。1.如图所示,这是一块大家常用的一种橡皮,
如果AD=4厘米,CD=3厘米,BC=12厘米,
你能算出AB两点之间的距离吗?拓展题2、等腰三角形底边上的高为8,周长为32,求这个三角形的面积8DABC解:设这个三角形为ABC,高为AD,设BD为X,则AB为(16-X), 由勾股定理得:
X2+82=(16-X)2即X2+64=256-32X+X2∴ X=6∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48再见勾股定理复习(第二课时) 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形a2=c2-b2b2 =c2-a2a2+b2=c2
一. 赛一赛,看谁准 1.下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ;(5)a=2m b=m2-1 c=m2+1是∠ C=900考点二:勾股定理的逆定理应用 2.小明向东走80m后,又走了60m,再走100m回到原地,小明向东走80m后,又向 方向走的.南或北3.已知:数7和24,请你再写一个整数,
使这些数恰好是一个直角三角形三边的长,
则这个数可以是——254.命题“直角三角形中30°角所对的直角边等于斜边的一半”的逆命题是
。 直角三角形中,如果一条直角边等于斜边的一半,
那么这条直角边所对角等于300.2. 观察下列几组数据:(1) 8, 15, 17; (2) 7, 12, 15; (3)12, 15, 20; (4) 7, 24, 25. 其中能作为直角三角形三边长的有( )组
A. 1 B. 2 C. 3 D. 44、直角三角形有一条直角边的长为11,另外两边的长也是正整数,则此三角形的周长是( )
A、120 B、121 C、132 D、1231.下列各组数中,以a,b,c为边的三角形不是
Rt△的是( )
A、a=1.5,b=2,c=3 B、a=7,b=24,c=25
C、a=6,b=8,c=10 D、a=3,b=4,c=5(二)、选择题AB3.一个三角形的三边之比为3:4:5,则这个三角形三边上的高
之比为( )
A. 3:4:5 B. 5:4:3 C. 20:15:12 D. 10:8:3CC例1、△ABC中,AB=13cm,BC=10cm,
BC边上的中线AD=12cm,
试判断△ABC的形状解:∵AD是BC边上的中线,BC=10
∴BD=CD=5
在△ABD中,BD=5,AD=12,
AB=13
∴BD2+AD2=AB2
∴∠ADB= ∠ADC=90 °
∴AC2=CD2+AD2=169,
∴AC=13=AB
∴ △ABC是等腰三角形
考点三:运用勾股定理及逆定理证明与计算例2、如图,在正方形ABDC中,E是CD的中点,F为BD上一点,且BF=3FD,试猜想线段AE,EF的位置关系并证明.解: AE⊥EF
设FD=1则BF=3,BD=AB=
AC=CD=4 DE=CE=2
在Rt△ABF中,AF2=AB2+BF2=25
在Rt △ DEF中,EF2=DF2+DE2=5
在Rt △ AEC,AE2=AC2+EC2=20
∴EF2+AE2=AF2
∴∠AEF=900 , ∴AE⊥EF例3.下列图①、②、③中的阴影部分分别是以直角三角形的三边为边长所作的正多边形;图④中的阴影部分分别是以直角三角形的三边为直径所作的半圆。根据勾股定理可知:分别以直角三角形的两条直角边为边长的正方形面积之和等于以斜边为边长的正方形的面积(如图②)
(1)类似的结论,对于图②的结论,对于图①、③、④是否成立?如果成立,请选择其中一个图形进行证明。
(2)根据(1)的结论,你能提出一般性的结论吗?写出你的结论并给予证明。 思考题:
已知?ABC的三边a, b ,c满足:
a2+b2+c2+338=10a+24b+26c,
请你判断?ABC的形状, 并说明理由.考考你! 你能分别在下列正方形中画出格点三角形,使它是直角三角形,且各顶点在正方形的三条边上(没有两点在正方形的同一边上).并能给予说明吗?有一块菜地,形状如下,
试求它的面积.(单位:米)试一试8、在△ABC中,∠BAC=120°,AB=AC= cm,一动点P从B向C以每秒2cm的速度移动,问当P点移动多少秒时,PA与腰垂直。 9、已知:如图,在△ABC中,∠C=60°,AB= ,AC=4,AD是BC边上的高,求BC的长。
