勾股定理全章教案[下学期]
文档属性
| 名称 | 勾股定理全章教案[下学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 45.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-07-27 00:00:00 | ||
图片预览



文档简介
课题: 18.1勾股定理 1
课型:新授课 课时:1
教学目的:
1.经历探索勾股定理及验证勾股定理的过程,培养推理能力,体会数形结合思想.
2.掌握勾股定理,了解利用拼图验证勾股定理(即面积法验证勾股定理).
3.灵活运用勾股定理解决实际问题.
教学重点:能熟练应用拼图法证明勾股定理
教学难点:用面积证明勾股定理
学前分析:
教学过程:
一、新课引入:
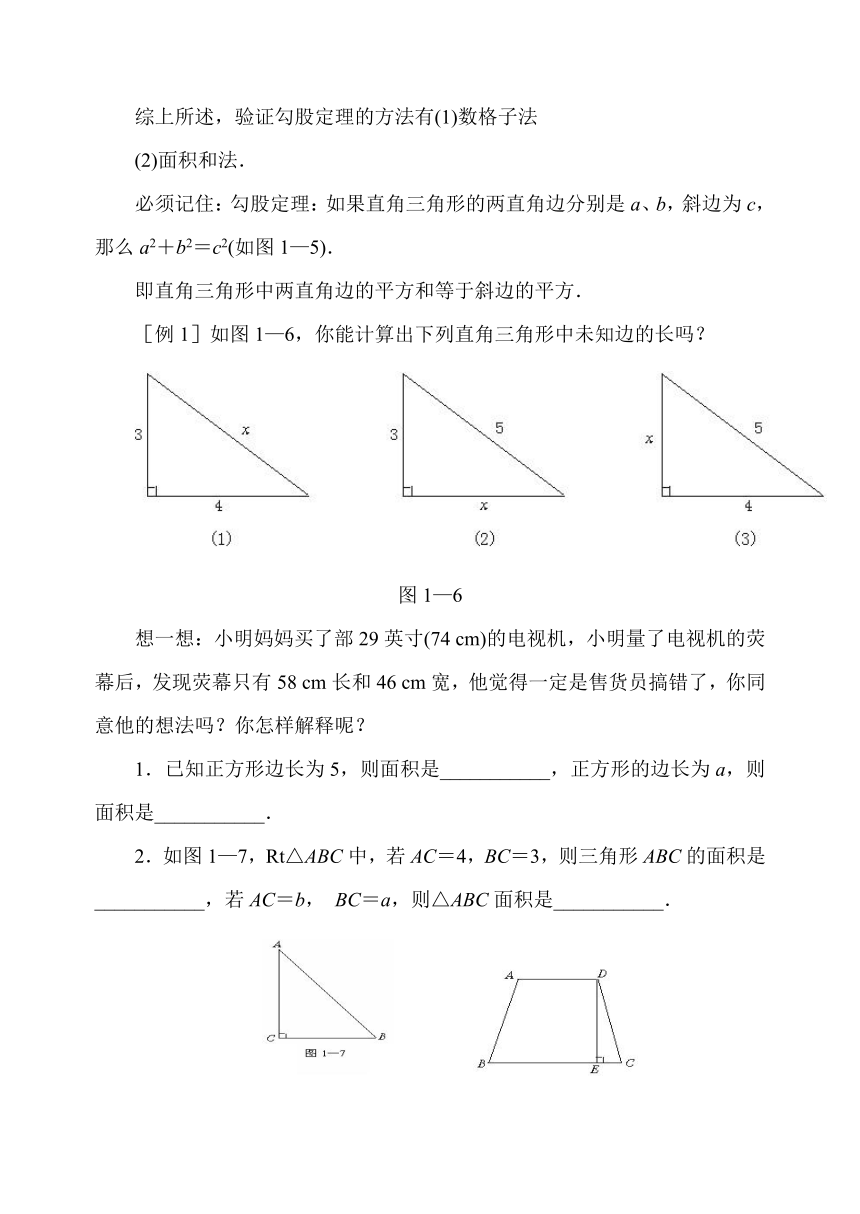
看下面的图,回答下列问题.
正方形的面积等于边长的平方.
1、观察图1—1.正方形A中有___________个小方格,即正方形A的面积是___________个单位面积.正方形B中有___________个小方格,即正方形B的面积有___________个单位面积.正方形C中有___________个小方格,即C的面积有___________个单位面积.
2、用同样的方法你能得到图1—2中正方形A、B、C中各含有多少个小方格?它们的面积是多少?
二、新课讲解:
你猜想正确吗?答案是a2+b2=c2.
问题一:观察图1—3、图1—4,并填写下表:
A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)
图1—3
图1—4
问题二:三个小正方形A、B、C的面积之间的关系.
问题三:你发现了直角三角形三边之间的长之间有什么关系吗?
问题四:你以5 cm、12 cm为直角边再做一个直角三角形,并测量斜边的长度,问题三中的规律对这个三角形还成立吗?
你解决了这几个问题了吗?我们对一下答案吧,看你是否做对喽!
问题一:图1—5中,正方形A有16个面积单位,正方形B有9个面积单位,正方形C有25个面积单位.
图1—4中,正方形A有4个面积单位,正方形B有9个面积单位,正方形C有13个面积单位.
问题二:C面积=A面积+B面积.
问题三:
问题四:还是成立的.
综上所述,验证勾股定理的方法有(1)数格子法
(2)面积和法.
必须记住:勾股定理:如果直角三角形的两直角边分别是a、b,斜边为c,那么a2+b2=c2(如图1—5).
即直角三角形中两直角边的平方和等于斜边的平方.
[例1]如图1—6,你能计算出下列直角三角形中未知边的长吗?
图1—6
想一想:小明妈妈买了部29英寸(74 cm)的电视机,小明量了电视机的荧幕后,发现荧幕只有58 cm长和46 cm宽,他觉得一定是售货员搞错了,你同意他的想法吗?你怎样解释呢?
1.已知正方形边长为5,则面积是___________,正方形的边长为a,则面积是___________.
2.如图1—7,Rt△ABC中,若AC=4,BC=3,则三角形ABC的面积是___________,若AC=b, BC=a,则△ABC面积是___________.
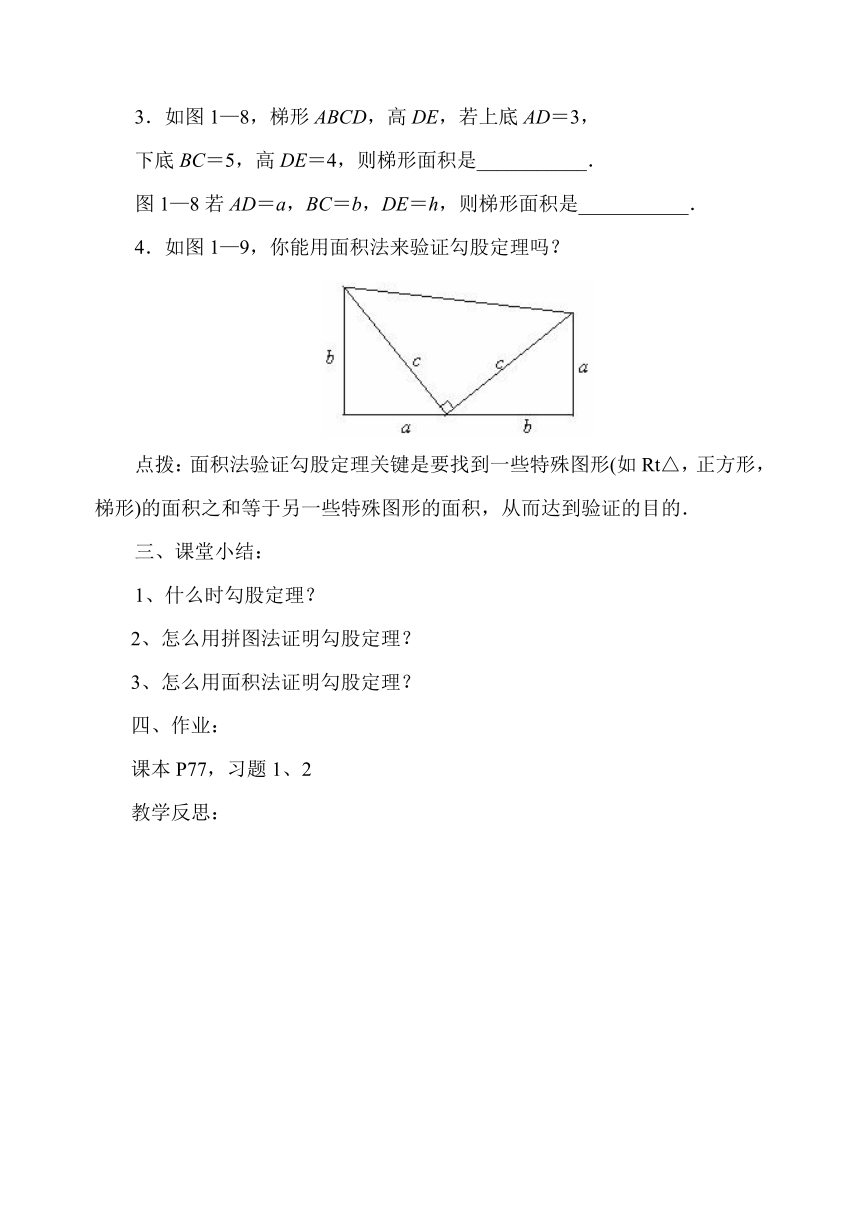
3.如图1—8,梯形ABCD,高DE,若上底AD=3,
下底BC=5,高DE=4,则梯形面积是___________.
图1—8若AD=a,BC=b,DE=h,则梯形面积是___________.
4.如图1—9,你能用面积法来验证勾股定理吗?
点拨:面积法验证勾股定理关键是要找到一些特殊图形(如Rt△,正方形,梯形)的面积之和等于另一些特殊图形的面积,从而达到验证的目的.
三、课堂小结:
1、什么时勾股定理?
2、怎么用拼图法证明勾股定理?
3、怎么用面积法证明勾股定理?
四、作业:
课本P77,习题1、2
教学反思:
课题: 18.1勾股定理 2
课型:新授课 课时:1
教学目的:
1、掌握直角三角形的判别条件,并能进行简单应用;
2、进一步发展数感,增加对勾股数的直观体验,培养从实际问题抽象出数学问题的能力,建立数学模型.
3、会通过边长判断一个三角形是否是直角三角形,并会辨析哪些问题应用哪个结论.
教学重点:运用身边熟悉的事物,从多种角度发展数感,会通过边长判断一个三角形是否是直角三角形,并会辨析哪些问题应用哪个结论.
教学难点:会辨析哪些问题应用哪个结论.
学前分析:
教学过程:
一、新课引入:
请学生复述勾股定理;使用勾股定理的前提条件是什么?
已知△ABC的两边AB=5,AC=12,则BC=13对吗?
创设问题情景:由课前准备好的一组学生以小品的形式演示教材第9页古埃及造直角的方法.
这样做得到的是一个直角三角形吗?
提出课题:能得到直角三角形吗
二、新课讲解:
⒈如何来判断?(用直角三角板检验)
这个三角形的三边分别是多少?(一份视为1)它们之间存在着怎样的关系?
就是说,如果三角形的三边为,,,请猜想在什么条件下,以这三边组成的三角形是直角三角形?(当满足较小两边的平方和等于较大边的平方时)
⒉继续尝试:下面的三组数分别是一个三角形的三边长a,b,c:
5,12,13; 6, 8, 10; 8,15,17.
(1)这三组数都满足a2 +b2=c2吗?
(2)分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
⒊直角三角形判定定理:如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
⒋例1 一个零件的形状如左图所示,按规定这个零件中 ∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如右图所示,这个零件符合要求吗?
随堂练习:
1、下列几组数能否作为直角三角形的三边长?说说你的理由.
⑴9,12,15; ⑵15,36,39;
⑶12,35,36; ⑷12,18,22.
2、已知 ABC中BC=41, AC=40, AB=9, 则此三角形为_______三角形, ______是最大角.
4、四边形ABCD中已知AB=3,BC=4,CD=12,DA=13,且∠ABC=900,求这个四边形的面积.
4、习题1.3
三、课堂小结:
⒈直角三角形判定定理:如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么这个三角形是直角三角形.
⒉满足a2 +b2=c2的三个正整数,称为勾股数.勾股数扩大相同倍数后,仍为勾股数.
四、作业:
P78习题3、4、5
教学反思:
课题: 18.1勾股定理3
课型: 新授课 课时:1
教学目的:
1、能运用勾股定理及直角三角形的判别条件(即勾股定理的逆定理)解决简单的实际问题.
2、通过本节学习,使学生真正体会数学来源于生活,又应用于生活,增加如何在日常生活中用数学知识解决问题的经验和感受.
3、如何将数学知识应用于生活实际,如何选择适当的数学模型解决数学问题.
教学重点:能运用勾股定理及直角三角形的判别条件解决简单的实际问题.
教学难点:能运用勾股定理及直角三角形的判别条件解决简单的实际问题.
学前分析;
教学过程:
一 、新课引入:
前几节课我们学习了勾股定理,你还记得它有什么作用吗?
欲登12米高的建筑物,为安全需要,需使梯子底端离建筑物5米,至少需多长的梯子?
这个问题我们用勾股定理获得了解决,许多同学都能想到.但在日常生活中,针对某个问题应该怎样选择相应的数学知识去解决,不是很明显,就算你知道了用哪个定理去解决,怎样解决还是个问题?今天我们就来研究这个问题.
提出课题:1.3蚂蚁怎样走最近
二、新课讲解:
C
⒈出示问题1:有一个圆柱,它的高等于12厘米,底面半径等于3厘米.在圆行柱的底面A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的的最短路程是多少?(π的值取3).
(1)同学们可自己做一个圆柱,尝试从A点到B点沿圆柱的侧面画出几条路线,你觉得哪条路线最短呢?(小组讨论)
(2)如图,将圆柱侧面剪开展开成一个长方形,从A点到B 点的最短路线是什么 你画对了吗
(3)蚂蚁从A点出发,想吃到B点上的食物,它沿圆柱侧面爬行的最短路程是多少?(学生分组讨论,公布结果)
⒉出示问题2:如图所示是一尊雕塑的底座的正面,李叔叔想要检测正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺.
(1)你能替他想办法完成任务吗?
(2)李叔叔量得AD的长是30厘米,AB的长是40厘米,BD长是50厘米.AD边垂直于AB边吗?
(3)小明随身只有一个长度为20厘米的刻度尺,他能有办法检验AD边是否垂直于AB边吗?BC边与AB边呢?
随堂练习:
1.第14页,第1题(教师与学生共同完成画图,学生独立完成解答过程,并公布结果)
甲、乙两位探险者到沙漠进行探险.某日早晨8∶00甲先出发,他以6千米/时的速度向东行走.1时后乙出发,他以5千米/时的速度向北行进.上午10∶00,甲、乙两人相距多远?
2.第15页,习题2;
3.第15页,习题3.
三、课堂小结:
⒈今天在解决数学问题时,我们用到了哪几个定理?
⒉通过今天的学习,你有什么收获?
四、作业:P78页7、8
教学反思:
课题: 18.3 勾股定理复习课
课型:新授课 课时:1
教学目的:
1、熟悉勾股定理的历史,进一步了解我国古代数学的伟大成就,培养探索知识的良好习惯。
2、掌握直角三角形三边、三角之间的关系,熟练地运用直角三角形的勾股定理和其他性质解决实际问题。
3、正确使用勾股定理的逆定理,准确地判断三角形的形状。
教学重点:
掌握勾股定理及其逆定理
教学难点:
准确应用勾股定理及其逆定理
学前分析:
教学过程:
一、复习:
1、直角三角形三边存在着什么关系?
2、直角三角形的角存在着什么关系?
3、直角三角形还有哪些性质?
4、如何判定一个三角形是直角三角形?
5、你知道勾股定理的历史吗?
二、知识点:
1、勾股定理:在探索中学习认识勾股定理 ,通过“数格子”和“拼图”等实践活动证明勾股定理
如果直角三角形两直角边分别为a, b,斜边为c,那么a2+b2=c2,即直角三角形两直角边的平方和等于斜边的平方.
2、勾股定理揭示了直角三角形之间的数量关系,并且是直角三角形的重要性质,应用广泛.在解直角三角形时,通常有以下几种情况:
(1)已知直角三角形的两边,求第三边;
(2)已知直角三角形的一边,求另两边的关系;
(3)证明三角形边长的平方关系;
(4)对勾股定理要学会灵活变形.如Rt△ABC中,∠C=90°,已知c,a求b时,应将勾股定理变化为b2=c2-a2等等.
3、勾股定理的逆定理.
如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.
4、勾股定理的逆定理是判定一个三角形是直角三角形的重要方法,它需要通过代数运算,“算”出具备直角三角形的重要关系,是用代数方法研究几何问题.
勾股定理的逆定理,在作图中有着较广泛的应用,可以用它来确定直角等.
了解“勾股数”的意义:即满足a2+b2=c2的三个正整数,称为勾股数.
三、例题:
例1、已知:如图,△ABC中,AD是中线,AE是高,AB=12,AC=8,BC=10.
求:DE的长.
解: 设EC=a, 则 BE=10-a.
Rt△AEC和Rt△ABE中 ,由勾股定理得
AE2=AC2-EC2=AB2-BE2,
∴ AE2=64-a2=122-(10-a)2.
解得 a=1.2.
故 DE=DC-EC=5-1.2=3.8.
例2、已知,如果四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
解:连结AC,Rt△ABC中,AC2=AB2+BC2=32+42=25,
∴ AC=5.
又△ACD中,∵ AC2+CD2=25+122=169,
而 AB2=132=169,
∴ AC2+CD2=AB2,∴ ∠ACD=90°.
故S四边形ABCD=S△ABC+S△ACD=AB·BC+AC·CD=×3×4+×5×12=6+30=36.
四、作业:卷子
教学反思:
练习:
一、判断题:
1、若a、b、c是ΔABC的三边,则。( )
2、若a、b、c是直角ΔABC的三边,则。( )
3、若正方形的面积为2,则它的对角线长为2cm。( )
4、ΔABC的两边AB=5,AC=12,则BC=13。( )
5、RtΔABC的两边a=6,b=8,则c=10。( )
6、由于0.3、0.4、0.5不是勾股数,所以以0.3、0.4、0.5为边长的三角形不是直角三角形。( )
7、由于以0.5、1.2、1.3为边长的三角形是直角三角形,所以0.5、1.2、1.3是勾股数。( )
二、填空题:
1、在RtΔABC中,∠C=90°,BC=12,SΔABC=30,则AB=__________。
2、等腰三角形的腰长AB=10cm,底BC为26cm,则底边上的高为___________,面积为________。
3、已知四边形ABCD中,AD∥BC,∠A=90°,AB=8,AD=4,BC=6,则以DC为边的正方形面积为_____________。
4、在ΔABC中,∠C=90°,(1)若a=5,b=12,则c=_______。(2)若c=41,a=9,则b=_____。
5、一个直角三角形的三边为三个连续偶数,则它的三边长分别为___________。
6、在ΔABC中,∠C=90°,AC=6,CB=8,则AB边上的高为_____________。
7、等边ΔABC的高为3cm,则以AB为边的正方形面积为__________。
8、已知三角形的三条边长分别为5、12、13,则这个三角形是__________________。
9、在RtΔABC中,∠C=90°,∠B=30°,AC=1,以BC为边的正方形面积为___________。
10、三条线段m、n、p满足:,这个三角形为___________________。
11、等腰三角形ABC的面积为12,底边上的高AD为3cm,则它的周长为__________。
三、选择题:
1、在ΔABC中,∠ACB=90°,AC=12,CB=5,M、N在AB上且AM=AC,BN=BC,则MN的长为( )
A、2 B、26 C、3 D、4
2、在ΔABC中,AB=15,AC=13,高AD=12,则ΔABC的周长为( )
A、42 B、32 C、42或32 D、37或33
3、等腰直角三角形斜边上的中线为5cm,则以直角边为边的正方形的面积为( )
A、10 B、15 C、50 D、25
4、分别以下列四组数为一个三角形的边长:(1)6、8、10;(2)5、12、13;(3)8、15、17;(4)4、5、6其中能构成直角三角形的有( )
A、4组 B、3组 C、2组 D、1组
四、解答题:
1、已知:ΔABC为直角三角形,且∠B=90°,D、E分别在BC和AB上,那么可以得到吗?为什么?
2、某车间的人字形屋架为等腰三角形ABC,跨度AB=24m,上弦AC=13m,求中柱CD。(D为底边AB的中点)
3、一艘渔船正以30海里/时的速度由西向东追赶渔群,在A处看见小岛C在船北偏东60°。40分钟后,渔船行至B处,此时看见小岛C在船的北偏东30°,已知小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区,问这艘渔船继续航行(追赶渔群),是否有进入危险区的可能?
4、等腰三角形的腰长为25,底为48,求它的面积。
5、一个矩形的抽斗长为24cm,宽为7cm,在里面放一根铁条,那铁条最长可以是多少?
6、操场上的旗杆高5米,从顶处拉一根长13米的绳子,使绳子拉直的另一端落在地上,问此绳子的下端离旗杆有多远。
7、四边形ABCD中,∠A=90°,AB=4,AD=3,CD=12,BC=13,求这个四边形的面积。
8、有一个小朋友拿着一根竹竿要通过一个长方形的门,如果把竹竿竖放就比门高出1尺,斜放就恰好等于门的对角线,已知门宽4尺,求竹竿高与门高。
课型:新授课 课时:1
教学目的:
1.经历探索勾股定理及验证勾股定理的过程,培养推理能力,体会数形结合思想.
2.掌握勾股定理,了解利用拼图验证勾股定理(即面积法验证勾股定理).
3.灵活运用勾股定理解决实际问题.
教学重点:能熟练应用拼图法证明勾股定理
教学难点:用面积证明勾股定理
学前分析:
教学过程:
一、新课引入:
看下面的图,回答下列问题.
正方形的面积等于边长的平方.
1、观察图1—1.正方形A中有___________个小方格,即正方形A的面积是___________个单位面积.正方形B中有___________个小方格,即正方形B的面积有___________个单位面积.正方形C中有___________个小方格,即C的面积有___________个单位面积.
2、用同样的方法你能得到图1—2中正方形A、B、C中各含有多少个小方格?它们的面积是多少?
二、新课讲解:
你猜想正确吗?答案是a2+b2=c2.
问题一:观察图1—3、图1—4,并填写下表:
A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)
图1—3
图1—4
问题二:三个小正方形A、B、C的面积之间的关系.
问题三:你发现了直角三角形三边之间的长之间有什么关系吗?
问题四:你以5 cm、12 cm为直角边再做一个直角三角形,并测量斜边的长度,问题三中的规律对这个三角形还成立吗?
你解决了这几个问题了吗?我们对一下答案吧,看你是否做对喽!
问题一:图1—5中,正方形A有16个面积单位,正方形B有9个面积单位,正方形C有25个面积单位.
图1—4中,正方形A有4个面积单位,正方形B有9个面积单位,正方形C有13个面积单位.
问题二:C面积=A面积+B面积.
问题三:
问题四:还是成立的.
综上所述,验证勾股定理的方法有(1)数格子法
(2)面积和法.
必须记住:勾股定理:如果直角三角形的两直角边分别是a、b,斜边为c,那么a2+b2=c2(如图1—5).
即直角三角形中两直角边的平方和等于斜边的平方.
[例1]如图1—6,你能计算出下列直角三角形中未知边的长吗?
图1—6
想一想:小明妈妈买了部29英寸(74 cm)的电视机,小明量了电视机的荧幕后,发现荧幕只有58 cm长和46 cm宽,他觉得一定是售货员搞错了,你同意他的想法吗?你怎样解释呢?
1.已知正方形边长为5,则面积是___________,正方形的边长为a,则面积是___________.
2.如图1—7,Rt△ABC中,若AC=4,BC=3,则三角形ABC的面积是___________,若AC=b, BC=a,则△ABC面积是___________.
3.如图1—8,梯形ABCD,高DE,若上底AD=3,
下底BC=5,高DE=4,则梯形面积是___________.
图1—8若AD=a,BC=b,DE=h,则梯形面积是___________.
4.如图1—9,你能用面积法来验证勾股定理吗?
点拨:面积法验证勾股定理关键是要找到一些特殊图形(如Rt△,正方形,梯形)的面积之和等于另一些特殊图形的面积,从而达到验证的目的.
三、课堂小结:
1、什么时勾股定理?
2、怎么用拼图法证明勾股定理?
3、怎么用面积法证明勾股定理?
四、作业:
课本P77,习题1、2
教学反思:
课题: 18.1勾股定理 2
课型:新授课 课时:1
教学目的:
1、掌握直角三角形的判别条件,并能进行简单应用;
2、进一步发展数感,增加对勾股数的直观体验,培养从实际问题抽象出数学问题的能力,建立数学模型.
3、会通过边长判断一个三角形是否是直角三角形,并会辨析哪些问题应用哪个结论.
教学重点:运用身边熟悉的事物,从多种角度发展数感,会通过边长判断一个三角形是否是直角三角形,并会辨析哪些问题应用哪个结论.
教学难点:会辨析哪些问题应用哪个结论.
学前分析:
教学过程:
一、新课引入:
请学生复述勾股定理;使用勾股定理的前提条件是什么?
已知△ABC的两边AB=5,AC=12,则BC=13对吗?
创设问题情景:由课前准备好的一组学生以小品的形式演示教材第9页古埃及造直角的方法.
这样做得到的是一个直角三角形吗?
提出课题:能得到直角三角形吗
二、新课讲解:
⒈如何来判断?(用直角三角板检验)
这个三角形的三边分别是多少?(一份视为1)它们之间存在着怎样的关系?
就是说,如果三角形的三边为,,,请猜想在什么条件下,以这三边组成的三角形是直角三角形?(当满足较小两边的平方和等于较大边的平方时)
⒉继续尝试:下面的三组数分别是一个三角形的三边长a,b,c:
5,12,13; 6, 8, 10; 8,15,17.
(1)这三组数都满足a2 +b2=c2吗?
(2)分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
⒊直角三角形判定定理:如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
⒋例1 一个零件的形状如左图所示,按规定这个零件中 ∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如右图所示,这个零件符合要求吗?
随堂练习:
1、下列几组数能否作为直角三角形的三边长?说说你的理由.
⑴9,12,15; ⑵15,36,39;
⑶12,35,36; ⑷12,18,22.
2、已知 ABC中BC=41, AC=40, AB=9, 则此三角形为_______三角形, ______是最大角.
4、四边形ABCD中已知AB=3,BC=4,CD=12,DA=13,且∠ABC=900,求这个四边形的面积.
4、习题1.3
三、课堂小结:
⒈直角三角形判定定理:如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么这个三角形是直角三角形.
⒉满足a2 +b2=c2的三个正整数,称为勾股数.勾股数扩大相同倍数后,仍为勾股数.
四、作业:
P78习题3、4、5
教学反思:
课题: 18.1勾股定理3
课型: 新授课 课时:1
教学目的:
1、能运用勾股定理及直角三角形的判别条件(即勾股定理的逆定理)解决简单的实际问题.
2、通过本节学习,使学生真正体会数学来源于生活,又应用于生活,增加如何在日常生活中用数学知识解决问题的经验和感受.
3、如何将数学知识应用于生活实际,如何选择适当的数学模型解决数学问题.
教学重点:能运用勾股定理及直角三角形的判别条件解决简单的实际问题.
教学难点:能运用勾股定理及直角三角形的判别条件解决简单的实际问题.
学前分析;
教学过程:
一 、新课引入:
前几节课我们学习了勾股定理,你还记得它有什么作用吗?
欲登12米高的建筑物,为安全需要,需使梯子底端离建筑物5米,至少需多长的梯子?
这个问题我们用勾股定理获得了解决,许多同学都能想到.但在日常生活中,针对某个问题应该怎样选择相应的数学知识去解决,不是很明显,就算你知道了用哪个定理去解决,怎样解决还是个问题?今天我们就来研究这个问题.
提出课题:1.3蚂蚁怎样走最近
二、新课讲解:
C
⒈出示问题1:有一个圆柱,它的高等于12厘米,底面半径等于3厘米.在圆行柱的底面A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的的最短路程是多少?(π的值取3).
(1)同学们可自己做一个圆柱,尝试从A点到B点沿圆柱的侧面画出几条路线,你觉得哪条路线最短呢?(小组讨论)
(2)如图,将圆柱侧面剪开展开成一个长方形,从A点到B 点的最短路线是什么 你画对了吗
(3)蚂蚁从A点出发,想吃到B点上的食物,它沿圆柱侧面爬行的最短路程是多少?(学生分组讨论,公布结果)
⒉出示问题2:如图所示是一尊雕塑的底座的正面,李叔叔想要检测正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺.
(1)你能替他想办法完成任务吗?
(2)李叔叔量得AD的长是30厘米,AB的长是40厘米,BD长是50厘米.AD边垂直于AB边吗?
(3)小明随身只有一个长度为20厘米的刻度尺,他能有办法检验AD边是否垂直于AB边吗?BC边与AB边呢?
随堂练习:
1.第14页,第1题(教师与学生共同完成画图,学生独立完成解答过程,并公布结果)
甲、乙两位探险者到沙漠进行探险.某日早晨8∶00甲先出发,他以6千米/时的速度向东行走.1时后乙出发,他以5千米/时的速度向北行进.上午10∶00,甲、乙两人相距多远?
2.第15页,习题2;
3.第15页,习题3.
三、课堂小结:
⒈今天在解决数学问题时,我们用到了哪几个定理?
⒉通过今天的学习,你有什么收获?
四、作业:P78页7、8
教学反思:
课题: 18.3 勾股定理复习课
课型:新授课 课时:1
教学目的:
1、熟悉勾股定理的历史,进一步了解我国古代数学的伟大成就,培养探索知识的良好习惯。
2、掌握直角三角形三边、三角之间的关系,熟练地运用直角三角形的勾股定理和其他性质解决实际问题。
3、正确使用勾股定理的逆定理,准确地判断三角形的形状。
教学重点:
掌握勾股定理及其逆定理
教学难点:
准确应用勾股定理及其逆定理
学前分析:
教学过程:
一、复习:
1、直角三角形三边存在着什么关系?
2、直角三角形的角存在着什么关系?
3、直角三角形还有哪些性质?
4、如何判定一个三角形是直角三角形?
5、你知道勾股定理的历史吗?
二、知识点:
1、勾股定理:在探索中学习认识勾股定理 ,通过“数格子”和“拼图”等实践活动证明勾股定理
如果直角三角形两直角边分别为a, b,斜边为c,那么a2+b2=c2,即直角三角形两直角边的平方和等于斜边的平方.
2、勾股定理揭示了直角三角形之间的数量关系,并且是直角三角形的重要性质,应用广泛.在解直角三角形时,通常有以下几种情况:
(1)已知直角三角形的两边,求第三边;
(2)已知直角三角形的一边,求另两边的关系;
(3)证明三角形边长的平方关系;
(4)对勾股定理要学会灵活变形.如Rt△ABC中,∠C=90°,已知c,a求b时,应将勾股定理变化为b2=c2-a2等等.
3、勾股定理的逆定理.
如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.
4、勾股定理的逆定理是判定一个三角形是直角三角形的重要方法,它需要通过代数运算,“算”出具备直角三角形的重要关系,是用代数方法研究几何问题.
勾股定理的逆定理,在作图中有着较广泛的应用,可以用它来确定直角等.
了解“勾股数”的意义:即满足a2+b2=c2的三个正整数,称为勾股数.
三、例题:
例1、已知:如图,△ABC中,AD是中线,AE是高,AB=12,AC=8,BC=10.
求:DE的长.
解: 设EC=a, 则 BE=10-a.
Rt△AEC和Rt△ABE中 ,由勾股定理得
AE2=AC2-EC2=AB2-BE2,
∴ AE2=64-a2=122-(10-a)2.
解得 a=1.2.
故 DE=DC-EC=5-1.2=3.8.
例2、已知,如果四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
解:连结AC,Rt△ABC中,AC2=AB2+BC2=32+42=25,
∴ AC=5.
又△ACD中,∵ AC2+CD2=25+122=169,
而 AB2=132=169,
∴ AC2+CD2=AB2,∴ ∠ACD=90°.
故S四边形ABCD=S△ABC+S△ACD=AB·BC+AC·CD=×3×4+×5×12=6+30=36.
四、作业:卷子
教学反思:
练习:
一、判断题:
1、若a、b、c是ΔABC的三边,则。( )
2、若a、b、c是直角ΔABC的三边,则。( )
3、若正方形的面积为2,则它的对角线长为2cm。( )
4、ΔABC的两边AB=5,AC=12,则BC=13。( )
5、RtΔABC的两边a=6,b=8,则c=10。( )
6、由于0.3、0.4、0.5不是勾股数,所以以0.3、0.4、0.5为边长的三角形不是直角三角形。( )
7、由于以0.5、1.2、1.3为边长的三角形是直角三角形,所以0.5、1.2、1.3是勾股数。( )
二、填空题:
1、在RtΔABC中,∠C=90°,BC=12,SΔABC=30,则AB=__________。
2、等腰三角形的腰长AB=10cm,底BC为26cm,则底边上的高为___________,面积为________。
3、已知四边形ABCD中,AD∥BC,∠A=90°,AB=8,AD=4,BC=6,则以DC为边的正方形面积为_____________。
4、在ΔABC中,∠C=90°,(1)若a=5,b=12,则c=_______。(2)若c=41,a=9,则b=_____。
5、一个直角三角形的三边为三个连续偶数,则它的三边长分别为___________。
6、在ΔABC中,∠C=90°,AC=6,CB=8,则AB边上的高为_____________。
7、等边ΔABC的高为3cm,则以AB为边的正方形面积为__________。
8、已知三角形的三条边长分别为5、12、13,则这个三角形是__________________。
9、在RtΔABC中,∠C=90°,∠B=30°,AC=1,以BC为边的正方形面积为___________。
10、三条线段m、n、p满足:,这个三角形为___________________。
11、等腰三角形ABC的面积为12,底边上的高AD为3cm,则它的周长为__________。
三、选择题:
1、在ΔABC中,∠ACB=90°,AC=12,CB=5,M、N在AB上且AM=AC,BN=BC,则MN的长为( )
A、2 B、26 C、3 D、4
2、在ΔABC中,AB=15,AC=13,高AD=12,则ΔABC的周长为( )
A、42 B、32 C、42或32 D、37或33
3、等腰直角三角形斜边上的中线为5cm,则以直角边为边的正方形的面积为( )
A、10 B、15 C、50 D、25
4、分别以下列四组数为一个三角形的边长:(1)6、8、10;(2)5、12、13;(3)8、15、17;(4)4、5、6其中能构成直角三角形的有( )
A、4组 B、3组 C、2组 D、1组
四、解答题:
1、已知:ΔABC为直角三角形,且∠B=90°,D、E分别在BC和AB上,那么可以得到吗?为什么?
2、某车间的人字形屋架为等腰三角形ABC,跨度AB=24m,上弦AC=13m,求中柱CD。(D为底边AB的中点)
3、一艘渔船正以30海里/时的速度由西向东追赶渔群,在A处看见小岛C在船北偏东60°。40分钟后,渔船行至B处,此时看见小岛C在船的北偏东30°,已知小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区,问这艘渔船继续航行(追赶渔群),是否有进入危险区的可能?
4、等腰三角形的腰长为25,底为48,求它的面积。
5、一个矩形的抽斗长为24cm,宽为7cm,在里面放一根铁条,那铁条最长可以是多少?
6、操场上的旗杆高5米,从顶处拉一根长13米的绳子,使绳子拉直的另一端落在地上,问此绳子的下端离旗杆有多远。
7、四边形ABCD中,∠A=90°,AB=4,AD=3,CD=12,BC=13,求这个四边形的面积。
8、有一个小朋友拿着一根竹竿要通过一个长方形的门,如果把竹竿竖放就比门高出1尺,斜放就恰好等于门的对角线,已知门宽4尺,求竹竿高与门高。
