新课程下的勾股定理[上学期]
文档属性
| 名称 | 新课程下的勾股定理[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 279.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-08-23 00:00:00 | ||
图片预览





文档简介
课件19张PPT。勾股定理学习目标1、理解勾股定理;
2、探究勾股定理的证明方法;
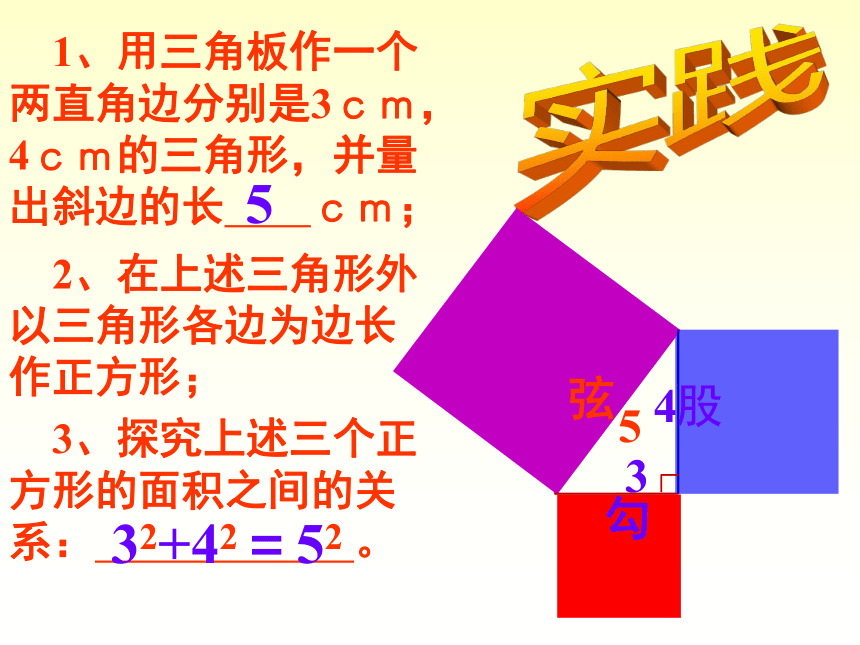
3、灵活应用勾股定理进行计算。 毕达哥拉斯生于2500年前的古希腊,是一位著名的哲学家、数学家、天文学家,他善于观察,勤于思考,往往能从平淡无奇的现象中发现深刻的道理。 一次,在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形的某种数量关系,由此发现了震铄古今的勾股定理 1、用三角板作一个两直角边分别是3cm,4cm的三角形,并量出斜边的长 cm; 2、在上述三角形外以三角形各边为边长作正方形; 3、探究上述三个正方形的面积之间的关系: 。实践345勾股弦532+42=52计算与观察结论:勾2+股2=弦2勾股定理
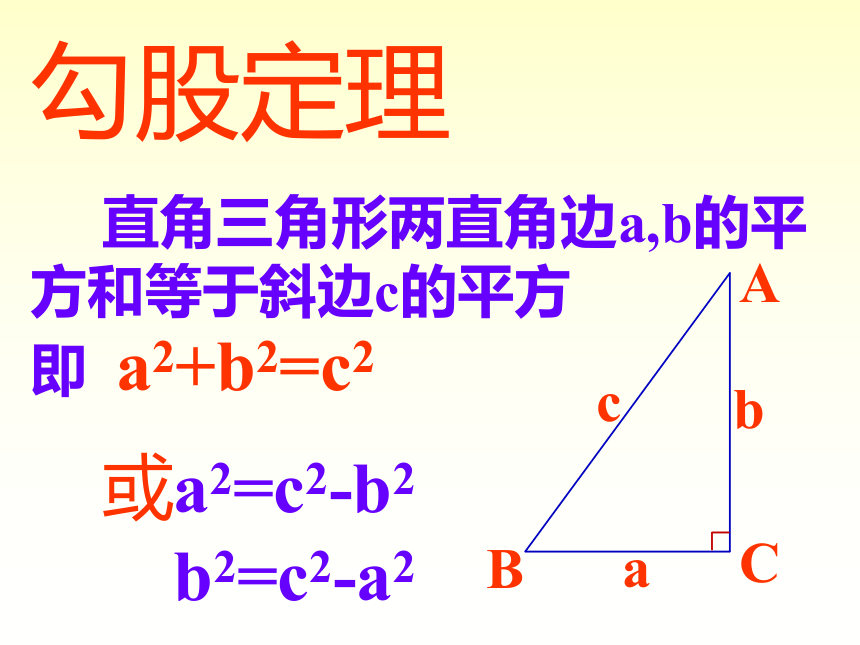
直角三角形两直角边a,b的平方和等于斜边c的平方 即 a2+b2=c2或a2=c2-b2
b2=c2-a2 勾股定理不仅是最古老的数学定理之一,也是数学中证法最多的一个定理。几千年来,人们已经发现了500多种不同的证明方法,足以编成厚厚的一本书。
我国清朝的康熙皇帝和美国第20届总统加菲尔德也证明过勾股定理。
宇宙空间是否有其他智慧生命存在,华罗庚曾建议:把勾股图转化为信号发射到宇宙空间,如果有智慧生命存在,他们不可能不认识这个真理(1)(2)图(1)的面积为 ;拼图1图(2)的面积为 ;由面积相等得 。c2+2aba2+b2+2aba2+b2=c2正方形的面积从整体上看为 ;拼图2从分割的角度看为 ,也即等于 ;c22ab+(b-a)2a2+b2从而得到 。a2+b2=c2 我国三国时期的数学家给出了更“绝”的证明,人们把这个图叫“赵爽弦图”你想知道他怎么证明吗? 归纳:
你能总结出这些证明方法的共同点吗? 从两个不同的角度计算同一个图形的面积,这两种方法计算的面积相等就得出 a2+b2=c2 课堂练习(一)
1、判断下列命题是否正确
①在△ABC中,∠A=30°,则a2+b2=c2 [ ]
②在Rt△ABC中,∠B=90°,则a2+b2=c2 [ ]
③在Rt△ABC中,∠C=90°,a=3,b=2,则
c= a2+b2=32+22=13 [ ]×××公式变形:
c= b= a=课堂练习(二)
在Rt△ABC中,∠C=90°
1.已知a=12,b=16,则c= ,
2.已知a=6,c=10, 则b= ,
3.已知c=25,b=15,则a= ,20820 如图,一根旗杆在离地面9米处断裂,旗杆顶部在离旗杆底部12米处.旗杆折断之前有多高?912巩固练习
在Rt△ABC中,∠C=90°,AB=4
1.若∠A=30°,则BC= , AC= ;
2.若∠A=45°,则AC= ,BC= ; 2 思维拓展
已知直角三角形的两边分别为3和4,则第三边为 。 小结:
1、用拼图法证明了勾股定理;
2、在直角三角形中,当已知两边求第三边时,利用勾股定理。再见
2、探究勾股定理的证明方法;
3、灵活应用勾股定理进行计算。 毕达哥拉斯生于2500年前的古希腊,是一位著名的哲学家、数学家、天文学家,他善于观察,勤于思考,往往能从平淡无奇的现象中发现深刻的道理。 一次,在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形的某种数量关系,由此发现了震铄古今的勾股定理 1、用三角板作一个两直角边分别是3cm,4cm的三角形,并量出斜边的长 cm; 2、在上述三角形外以三角形各边为边长作正方形; 3、探究上述三个正方形的面积之间的关系: 。实践345勾股弦532+42=52计算与观察结论:勾2+股2=弦2勾股定理
直角三角形两直角边a,b的平方和等于斜边c的平方 即 a2+b2=c2或a2=c2-b2
b2=c2-a2 勾股定理不仅是最古老的数学定理之一,也是数学中证法最多的一个定理。几千年来,人们已经发现了500多种不同的证明方法,足以编成厚厚的一本书。
我国清朝的康熙皇帝和美国第20届总统加菲尔德也证明过勾股定理。
宇宙空间是否有其他智慧生命存在,华罗庚曾建议:把勾股图转化为信号发射到宇宙空间,如果有智慧生命存在,他们不可能不认识这个真理(1)(2)图(1)的面积为 ;拼图1图(2)的面积为 ;由面积相等得 。c2+2aba2+b2+2aba2+b2=c2正方形的面积从整体上看为 ;拼图2从分割的角度看为 ,也即等于 ;c22ab+(b-a)2a2+b2从而得到 。a2+b2=c2 我国三国时期的数学家给出了更“绝”的证明,人们把这个图叫“赵爽弦图”你想知道他怎么证明吗? 归纳:
你能总结出这些证明方法的共同点吗? 从两个不同的角度计算同一个图形的面积,这两种方法计算的面积相等就得出 a2+b2=c2 课堂练习(一)
1、判断下列命题是否正确
①在△ABC中,∠A=30°,则a2+b2=c2 [ ]
②在Rt△ABC中,∠B=90°,则a2+b2=c2 [ ]
③在Rt△ABC中,∠C=90°,a=3,b=2,则
c= a2+b2=32+22=13 [ ]×××公式变形:
c= b= a=课堂练习(二)
在Rt△ABC中,∠C=90°
1.已知a=12,b=16,则c= ,
2.已知a=6,c=10, 则b= ,
3.已知c=25,b=15,则a= ,20820 如图,一根旗杆在离地面9米处断裂,旗杆顶部在离旗杆底部12米处.旗杆折断之前有多高?912巩固练习
在Rt△ABC中,∠C=90°,AB=4
1.若∠A=30°,则BC= , AC= ;
2.若∠A=45°,则AC= ,BC= ; 2 思维拓展
已知直角三角形的两边分别为3和4,则第三边为 。 小结:
1、用拼图法证明了勾股定理;
2、在直角三角形中,当已知两边求第三边时,利用勾股定理。再见
