勾股定理复习[下学期]
图片预览





文档简介
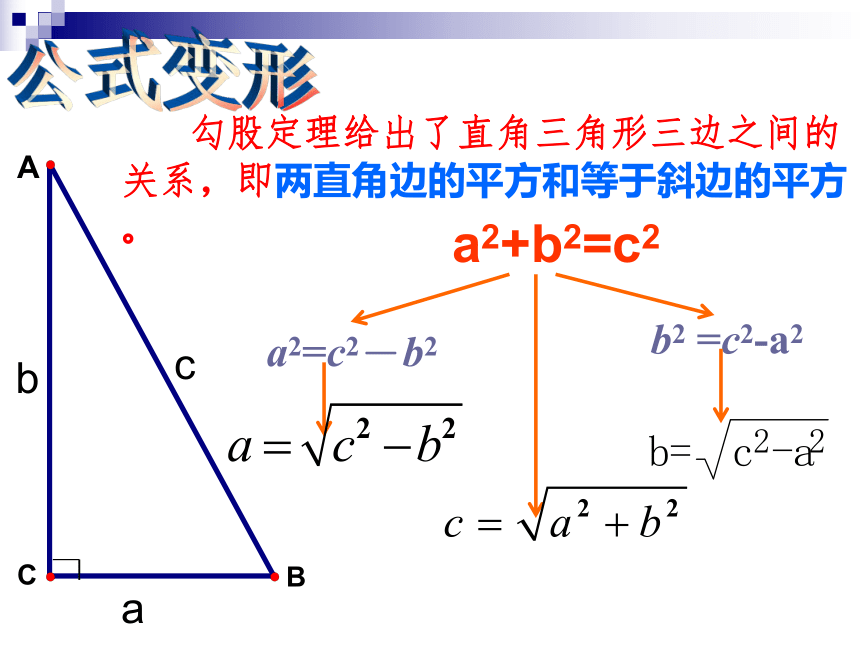
课件18张PPT。期末复习——勾股定理 如果直角三角形的两条直角边长分别为a、b,斜边为c,那么 a2 + b2 = c2 直角三角形两直角边的平方和等于斜边的平方。 注意:勾股定理只适用在直角三角形中求边之间的关系!什么叫勾股定理?知识回顾 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形a2=c2-b2b2 =c2-a2a2+b2=c2
练习:1、在Rt△ABC中,∠C=900
①若a=6,b=8, 则c=___;
②若a=40,c=41,则b=____;
③若a:b=1:2,c= 2 则S△ABC=____;
④若∠A=30°,a=2,则c=____,b=___,
a:b:c=_______;
⑤若∠A= ∠C,c= ,
则a=___,a:b:c=________.1094142.一根旗杆高8m,断裂后旗杆顶端落于旗杆底端4m处,旗杆的断裂出距离地面( )米。
33.小刚准备测量一段河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
A. 2m; B. 2.5m; C. 2.25m; D. 3m. A4. 直角三角形的两条直角边长为a,b,斜边上的高为h,则下列各式中总能成立的是 ( )D例1
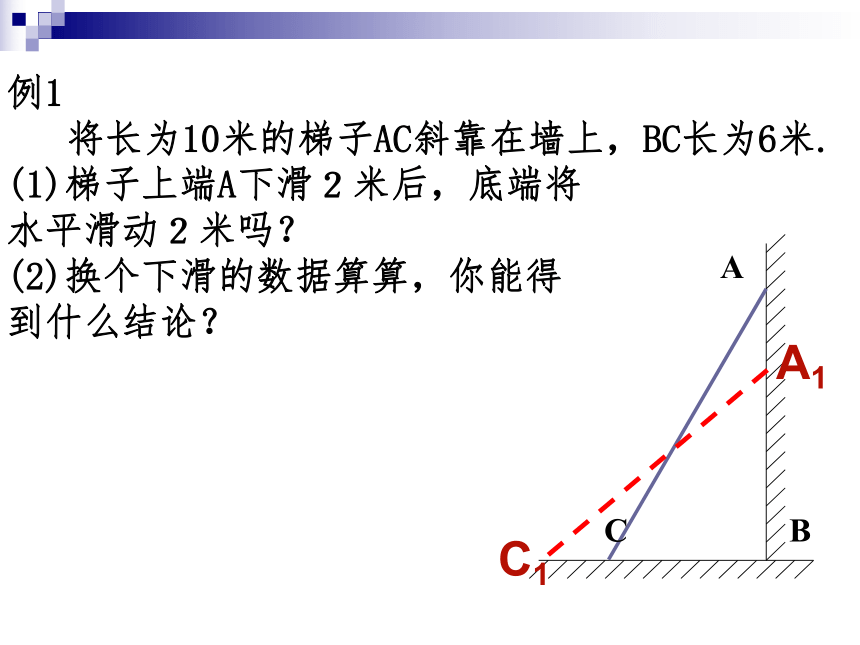
将长为10米的梯子AC斜靠在墙上,BC长为6米.
(1)梯子上端A下滑2米后,底端将
水平滑动2米吗?
(2)换个下滑的数据算算,你能得
到什么结论?ACBA1C1例2如图,将长方形ABCD沿着BD所在直线折叠,
BC交AD于点E,
(1)求证:△EBD是等腰三角形
(2)当AD=8,AB=4时,求△EBD的面积AECBD试一试如图,有一张直角三角形纸片,两
直角边长AC=6cm,BC=8cm,现将直角边
AC沿直线AD折叠,使它落在斜边AB上,且
与AE重合,则CD等于( )
A 2cm B 3cm C 4cm D 5cmBECADB68XX61048-X(8-X)2=X2+42解得:X=3
1、关于折叠问题,能得到:
(1)相等的线段,相等的角;
(2)全等三角形。
2、解这类题通常将一些未知的、
已知的元素挤入一个三角形中。 如果三角形的三边长边长a、b,c,
满足 a2 + b2 = c2 ,
那么这个三角形是直角三角形 根据三角形三边关系判断三角形的形状勾股定理的逆定理练习:1、下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ;(5)a=2m b=m2-1 c=m2+1是∠ C=900 ⒉ 小明向东走80m后,又走了60m,再走100m
回到原地,小明向东走80m后,又向
方向走的.南或北例1、△ABC中,AB=13cm,BC=10cm,
BC边上的中线AD=12cm,
试判断△ABC的形状解:∵AD是BC边上的中线,BC=10
∴BD=CD=5
在△ABD中,BD=5,AD=12,
AB=13
∴BD2+AD2=AB2
∴∠ADB= ∠ADC=90 °
∴AC2=CD2+AD2=169,
∴AC=13=AB
∴ △ABC是等腰三角形
勾股定理和它的逆定理的综合运用1、如图,正方形网格中的△ABC,若小方格边长为1,试判断△ABC的形状并说明理由。
在综合运用勾股定理及其逆定理时,需分清它们的条件与结论。例1、如图,在正方形ABDC中,E是CD的中点,F为BD上一点,且BF=3FD, 试猜想线段AE,EF的位置关系并证明.解: ∠AEF=900
设FD=1则BF=3,BD=AB=
AC=CD=4 DE=CE=2
在Rt△ABF中,AF2=AB2+BP2=25
在Rt △ DEF中,EF2=DF2+DE2=5
在Rt △ AEC,AE2=AC2+EC2=20
∴EF2+AE2=AF2
∴∠AEF=900考考你! 你能分别在下列正方形中画出格点三角形,使它是直角三角形,且各顶点在正方形的三条边上(没有两点在正方形的同一边上).并能给予说明吗?
练习:1、在Rt△ABC中,∠C=900
①若a=6,b=8, 则c=___;
②若a=40,c=41,则b=____;
③若a:b=1:2,c= 2 则S△ABC=____;
④若∠A=30°,a=2,则c=____,b=___,
a:b:c=_______;
⑤若∠A= ∠C,c= ,
则a=___,a:b:c=________.1094142.一根旗杆高8m,断裂后旗杆顶端落于旗杆底端4m处,旗杆的断裂出距离地面( )米。
33.小刚准备测量一段河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
A. 2m; B. 2.5m; C. 2.25m; D. 3m. A4. 直角三角形的两条直角边长为a,b,斜边上的高为h,则下列各式中总能成立的是 ( )D例1
将长为10米的梯子AC斜靠在墙上,BC长为6米.
(1)梯子上端A下滑2米后,底端将
水平滑动2米吗?
(2)换个下滑的数据算算,你能得
到什么结论?ACBA1C1例2如图,将长方形ABCD沿着BD所在直线折叠,
BC交AD于点E,
(1)求证:△EBD是等腰三角形
(2)当AD=8,AB=4时,求△EBD的面积AECBD试一试如图,有一张直角三角形纸片,两
直角边长AC=6cm,BC=8cm,现将直角边
AC沿直线AD折叠,使它落在斜边AB上,且
与AE重合,则CD等于( )
A 2cm B 3cm C 4cm D 5cmBECADB68XX61048-X(8-X)2=X2+42解得:X=3
1、关于折叠问题,能得到:
(1)相等的线段,相等的角;
(2)全等三角形。
2、解这类题通常将一些未知的、
已知的元素挤入一个三角形中。 如果三角形的三边长边长a、b,c,
满足 a2 + b2 = c2 ,
那么这个三角形是直角三角形 根据三角形三边关系判断三角形的形状勾股定理的逆定理练习:1、下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ;(5)a=2m b=m2-1 c=m2+1是∠ C=900 ⒉ 小明向东走80m后,又走了60m,再走100m
回到原地,小明向东走80m后,又向
方向走的.南或北例1、△ABC中,AB=13cm,BC=10cm,
BC边上的中线AD=12cm,
试判断△ABC的形状解:∵AD是BC边上的中线,BC=10
∴BD=CD=5
在△ABD中,BD=5,AD=12,
AB=13
∴BD2+AD2=AB2
∴∠ADB= ∠ADC=90 °
∴AC2=CD2+AD2=169,
∴AC=13=AB
∴ △ABC是等腰三角形
勾股定理和它的逆定理的综合运用1、如图,正方形网格中的△ABC,若小方格边长为1,试判断△ABC的形状并说明理由。
在综合运用勾股定理及其逆定理时,需分清它们的条件与结论。例1、如图,在正方形ABDC中,E是CD的中点,F为BD上一点,且BF=3FD, 试猜想线段AE,EF的位置关系并证明.解: ∠AEF=900
设FD=1则BF=3,BD=AB=
AC=CD=4 DE=CE=2
在Rt△ABF中,AF2=AB2+BP2=25
在Rt △ DEF中,EF2=DF2+DE2=5
在Rt △ AEC,AE2=AC2+EC2=20
∴EF2+AE2=AF2
∴∠AEF=900考考你! 你能分别在下列正方形中画出格点三角形,使它是直角三角形,且各顶点在正方形的三条边上(没有两点在正方形的同一边上).并能给予说明吗?
