第十八章 勾股定理(复习)[下学期]
文档属性
| 名称 | 第十八章 勾股定理(复习)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 101.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-06 00:00:00 | ||
图片预览






文档简介
课件14张PPT。第十八章 勾股定理(复习)回顾与思考
-----------勾股定理1、直角三角形的边、角之间分别存在着什么关系?2、如何判别一个三角形是否为直角三角形?
请你举例说明。3、互逆命题说出”等腰三角形的两个底角相等。“的逆命题。两个底角相等的三角形是等腰三角形。有两个角相等的三角形是等腰三角形。1、以下列各组线段为边长,能构成三角形的是 ;能构成直角三角形的是 ;
①3,4,5 ②1,3,4
③4,4,6 ④6,8,10
⑤5,7,2 ⑥13,5,12
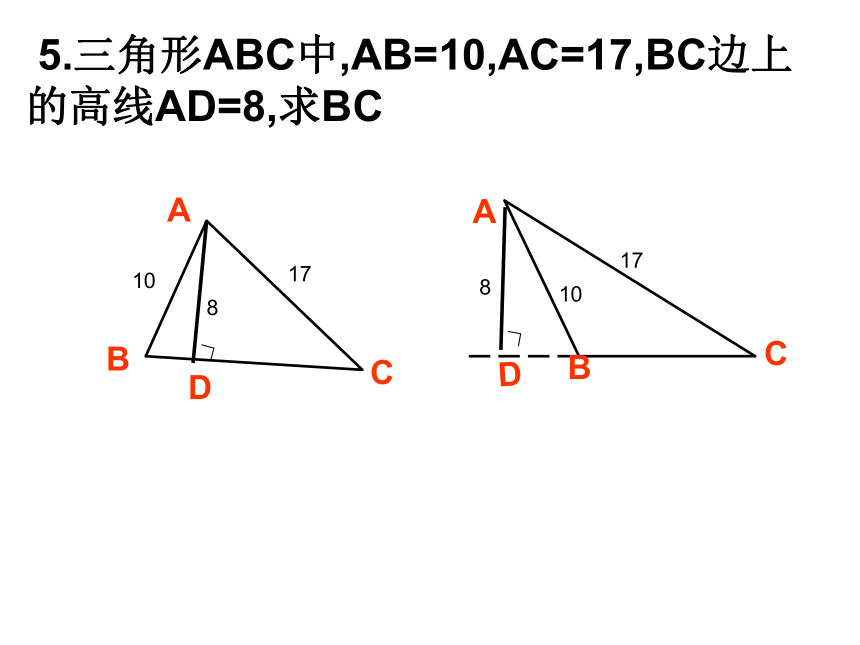
⑦7,25,24 ①③④⑥⑦①④⑥⑦C3、一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是 。4、(判断对错)? ABC的a=6,b=8,则c=10 ( )? 5.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC1017817108规律 分类思想 1.直角三角形中,已知两边长,而不知道是直角边、斜边时,应分类讨论。 2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。1.在Rt△ABC中,∠C=90°,CD 是高,AB=1,则 2 CD2 + AD2 +BD2 =____;2.三角形的三边长 a, b, c 满足
a2 +b2 +c2 +338 = 10a + 24b +26c,
此三角形为_____三角形.解:在Rt△ACD中
CD2+AD2=AC2……①
同理:CD2+BD2=BC2……②
①+②得:
2 CD2 + AD2 +BD2 =AC2+BC2
……
1直角 3、 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD3.长度分别为 3 , 4 , 5 , 12 ,13 的五根木棒能搭成(首尾连接)直角三角形的个数为( )
A 1个 B 2个 C 3个 D 4个BA5.在△ABC中,∠C=90°, ∠B=15°,DE垂直平分AB,
E为垂足,交BC边于D,BD=16cm,则DC=________.ABDEC6.在Rt △ABC中,∠C=90°, ∠A=30°,
a:b:c=_________,若∠A=45°, a:b:c=_________. 阅读下列解题过程: 已知a,b,c为△ABC的三边,且
满足a2c2-b2c2=a4-b4, 试判断△ABC的形状. 解∵ a2c2-b2c2=a4-b4 ① ∴ (a2-b2)c2=(a2+b2)(a2-b2) ② ∴ c2=a2+b2 ③ ∴ △ABC是直角三角形 问:上述解题过程,从哪一步开始出现错误?请写出该步的序号:______,错误的原因为:______________;本题正确的结论
是______________________ ③a2-b2可能为0直角三角形或等腰三角形 8.已知:在△ABC中,AB=13cm,BC=10cm,
BC边上的中线AD=12cm.
求证:AB=AC. 活动与探究
给出一组式子:32+42=52,82+62=102,
152+82=172,242+102=262.…
(1)你能发现上面式子的规律吗?请你用发现的规律,给
出第5个式子;
(2)请你证明你所发现的规律. 9.已知:在△ABC中,AB=AC=26, 点D是AC上一点,
CD=2,BD=10.
求: △ABC的面积 .
-----------勾股定理1、直角三角形的边、角之间分别存在着什么关系?2、如何判别一个三角形是否为直角三角形?
请你举例说明。3、互逆命题说出”等腰三角形的两个底角相等。“的逆命题。两个底角相等的三角形是等腰三角形。有两个角相等的三角形是等腰三角形。1、以下列各组线段为边长,能构成三角形的是 ;能构成直角三角形的是 ;
①3,4,5 ②1,3,4
③4,4,6 ④6,8,10
⑤5,7,2 ⑥13,5,12
⑦7,25,24 ①③④⑥⑦①④⑥⑦C3、一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是 。4、(判断对错)? ABC的a=6,b=8,则c=10 ( )? 5.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC1017817108规律 分类思想 1.直角三角形中,已知两边长,而不知道是直角边、斜边时,应分类讨论。 2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。1.在Rt△ABC中,∠C=90°,CD 是高,AB=1,则 2 CD2 + AD2 +BD2 =____;2.三角形的三边长 a, b, c 满足
a2 +b2 +c2 +338 = 10a + 24b +26c,
此三角形为_____三角形.解:在Rt△ACD中
CD2+AD2=AC2……①
同理:CD2+BD2=BC2……②
①+②得:
2 CD2 + AD2 +BD2 =AC2+BC2
……
1直角 3、 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD3.长度分别为 3 , 4 , 5 , 12 ,13 的五根木棒能搭成(首尾连接)直角三角形的个数为( )
A 1个 B 2个 C 3个 D 4个BA5.在△ABC中,∠C=90°, ∠B=15°,DE垂直平分AB,
E为垂足,交BC边于D,BD=16cm,则DC=________.ABDEC6.在Rt △ABC中,∠C=90°, ∠A=30°,
a:b:c=_________,若∠A=45°, a:b:c=_________. 阅读下列解题过程: 已知a,b,c为△ABC的三边,且
满足a2c2-b2c2=a4-b4, 试判断△ABC的形状. 解∵ a2c2-b2c2=a4-b4 ① ∴ (a2-b2)c2=(a2+b2)(a2-b2) ② ∴ c2=a2+b2 ③ ∴ △ABC是直角三角形 问:上述解题过程,从哪一步开始出现错误?请写出该步的序号:______,错误的原因为:______________;本题正确的结论
是______________________ ③a2-b2可能为0直角三角形或等腰三角形 8.已知:在△ABC中,AB=13cm,BC=10cm,
BC边上的中线AD=12cm.
求证:AB=AC. 活动与探究
给出一组式子:32+42=52,82+62=102,
152+82=172,242+102=262.…
(1)你能发现上面式子的规律吗?请你用发现的规律,给
出第5个式子;
(2)请你证明你所发现的规律. 9.已知:在△ABC中,AB=AC=26, 点D是AC上一点,
CD=2,BD=10.
求: △ABC的面积 .
