第八讲椭圆方程与离心率 专题学案-2022-2023学年高二上学期数学人教A版选修1-1(含答案)
文档属性
| 名称 | 第八讲椭圆方程与离心率 专题学案-2022-2023学年高二上学期数学人教A版选修1-1(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 525.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-29 00:00:00 | ||
图片预览




文档简介
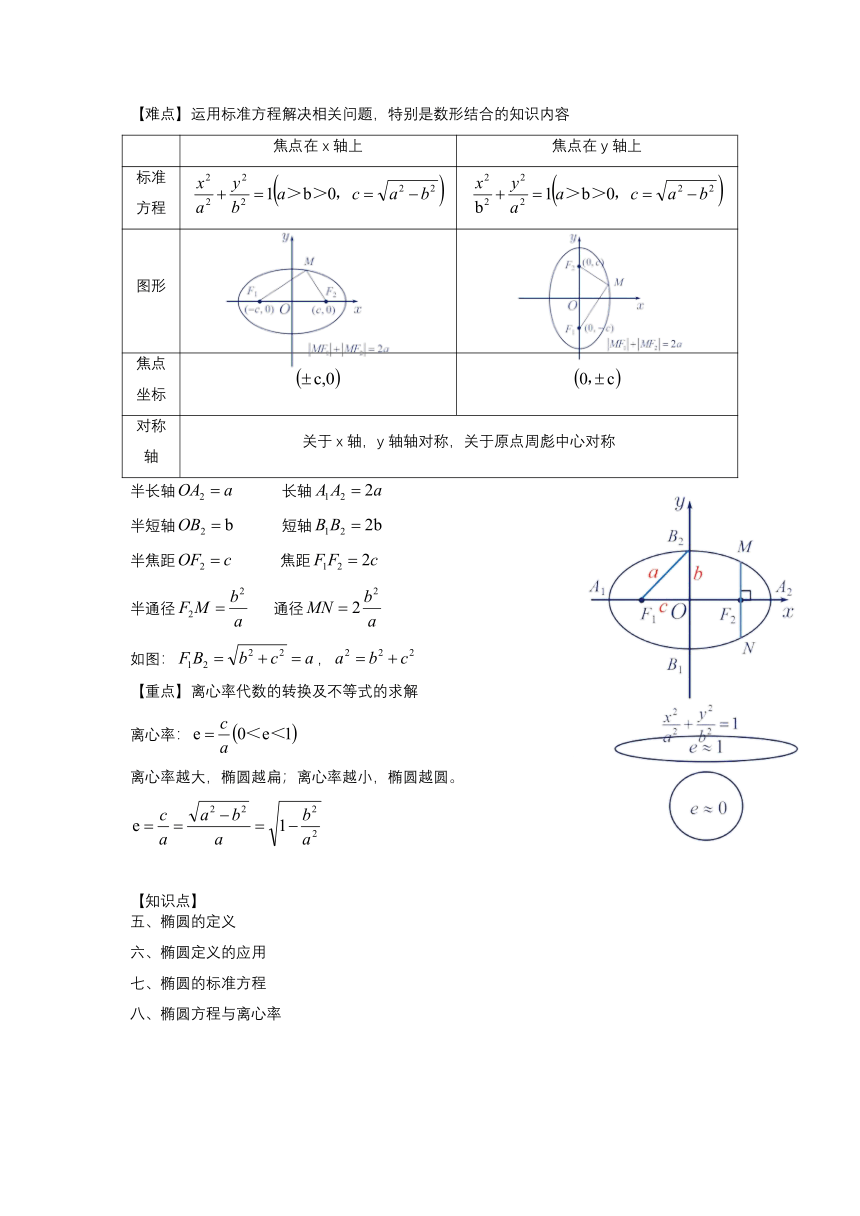
第八讲 椭圆方程与离心率
【学习目标】
理解椭圆的定义及椭圆的标准方程.
掌握用定义法和待定系数法求椭圆的标准方程.
理解椭圆方程与离心率之间的关系,能通过属性结合进行代数的求解离心率
【重点】椭圆的定义及椭圆的标准方程
【难点】运用标准方程解决相关问题,特别是数形结合的知识内容
焦点在x轴上 焦点在y轴上
标准方程
图形
焦点坐标
对称轴 关于x轴,y轴轴对称,关于原点周彪中心对称
半长轴 长轴
半短轴 短轴
半焦距 焦距
半通径 通径
如图:,
【重点】离心率代数的转换及不等式的求解
离心率:
离心率越大,椭圆越扁;离心率越小,椭圆越圆。
【知识点】
椭圆的定义
椭圆定义的应用
椭圆的标准方程
椭圆方程与离心率
【知识点】椭圆的定义
【例1】设P是椭圆上的点.若是椭圆的两个焦点,则等于( )
A.4 B.5 C.8 D.10
【课堂练习】
1、若椭圆上一点到其焦点的距离为6,则到另一焦点的距离为( )
A.4 B.194 C.94 D.14
【知识点】椭圆定义的运用
【例1】(2019福建高二期末)如果表示焦点在轴上的椭圆,那么实数的取值范围是( )
B. C. D.
【例2】过椭圆的一个焦点,且垂直于轴的直线被此椭圆截得的弦长为
【例3】直线被椭圆截得的弦长是( )
A. B. C. D.
【例4】已知点分别是椭圆的左、右焦点,点在此椭圆上,则的周长等于( )
A.20 B.16 C.18 D.14
【课堂练习】
1、如果方程表示焦点在x轴上的椭圆,则实数a的取值范围是( )
A. B. C.或 D.或
2、已知椭圆与直线交于,两点,且,则实数的值为( )
A. B. C. D.
3、已知P是椭圆上的一点,F1,F2是椭圆的两个焦点,且∠F1PF2=60°,则△F1PF2的面积是______.
【知识点】椭圆的标准方程
【例1】焦点在轴上,长轴长为,焦距为的椭圆标准方程;
【例2】与椭圆具有相同的离心率且过点的椭圆的标准方程
【课堂练习】
1、已知椭圆的上顶点为,右顶点为,若过原点作的垂线交椭圆的右准线于点,点到轴的距离为,则此椭圆的离心率为( )
A. B. C. D.
2、(安徽模拟)已知椭圆的左,右焦点分别为F1,F2,若在直线上x=2a存在点P使得线段PF1的垂直平分线过点F2,则离心率范围是
第八讲 椭圆方程与离心率
【学习目标】
理解椭圆的定义及椭圆的标准方程.
掌握用定义法和待定系数法求椭圆的标准方程.
理解椭圆方程与离心率之间的关系,能通过属性结合进行代数的求解离心率
【重点】椭圆的定义及椭圆的标准方程
【难点】运用标准方程解决相关问题,特别是数形结合的知识内容
焦点在x轴上 焦点在y轴上
标准方程
图形
焦点坐标
对称轴 关于x轴,y轴轴对称,关于原点周彪中心对称
半长轴 长轴
半短轴 短轴
半焦距 焦距
半通径 通径
如图:,
【重点】离心率代数的转换及不等式的求解
离心率:
离心率越大,椭圆越扁;离心率越小,椭圆越圆。
【知识点】
椭圆的定义
椭圆定义的应用
椭圆的标准方程
椭圆方程与离心率
【知识点】椭圆的定义
【例1】设P是椭圆上的点.若是椭圆的两个焦点,则等于( )
A.4 B.5 C.8 D.10
【答案】D
【分析】有椭圆的定义可得,椭圆上的点到焦点的距离之和是定长。
【详解】因为椭圆的方程为,所以a2=25,由椭圆的的定义知
【课堂练习】
1、若椭圆上一点到其焦点的距离为6,则到另一焦点的距离为( )
A.4 B.194 C.94 D.14
【答案】D
【分析】由椭圆的定义可得,椭圆上的点到焦点的距离之和是定长。
【详解】依题意,且
【知识点】椭圆定义的运用
【例1】(2019福建高二期末)如果表示焦点在轴上的椭圆,那么实数的取值范围是( )
B. C. D.
【答案】A
【分析】利用椭圆的定义,化简为标准方程,根据椭圆焦点所在轴的位置判断对应的a和b的大小。
【详解】
转化为椭圆的标准方程,得,因为表示焦点在y轴上的椭圆,所以,解得.所以实数k的取值范围是(0,1)
【例2】过椭圆的一个焦点,且垂直于轴的直线被此椭圆截得的弦长为
【答案】3
【分析】过椭圆的一个焦点,且求与焦点所在轴垂直的弦叫做椭圆的通径,其长
【详解】:,,所求弦长就是椭圆通径的长度
【例3】直线被椭圆截得的弦长是( )
A. B. C. D.
【答案】A
【分析】直线被椭圆截得的弦的长度求法公式:①;②.
解题时灵活选择,使得简化过程.
【详解】联立,得.
设直线被椭圆所截线段的两个端点分别为,.
思路1:
由韦达定理,得,,则
.
思路2:
解方程,得,,则
===.
【例4】已知点分别是椭圆的左、右焦点,点在此椭圆上,则的周长等于( )
A.20 B.16 C.18 D.14
【答案】C
【分析】根据椭圆的定义得出a,b,c,画出草图即可求得周长所对应的线段长度,灵活利用a,b,c,三者之间的关系。
【详解】根据椭圆方程可知,根据椭圆的定义可知,的周长为
【课堂练习】
1、如果方程表示焦点在x轴上的椭圆,则实数a的取值范围是( )
A. B. C.或 D.或
【答案】D
【分析】利用椭圆的交点在x轴上,能得到长半轴大于短半轴,从而得到不等式,解不等式时需要注意长半轴和短半轴需同时满足大于0.
【详解】椭圆的焦点在轴上,,解得或,故选D.
2、已知椭圆与直线交于,两点,且,则实数的值为( )
A. B. C. D.
【答案】A
【分析】对于此题,弦长公式选择“”,计算相对方便
【详解】联立方程组,消,得.
>0,16>0,.
设,,根据韦达定理,有,.
,,=,.
,符合.
3、已知P是椭圆上的一点,F1,F2是椭圆的两个焦点,且∠F1PF2=60°,则△F1PF2的面积是______.
【答案】
【分析】根据椭圆的定义画出草图,根据图像可以得到三角形的图形关系示意图,灵活运用余弦定理可以求得面积。
【解析】∵|PF1|+|PF2|=4,,又∵∠F1PF2=60°,
由余弦定理可得|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos60°
12=(|PF1|+|PF2|)2-2|PF1|·|PF2|-|PF1|·|PF2|,∴,
∴.
【知识点】椭圆的标准方程
【例1】焦点在轴上,长轴长为,焦距为的椭圆标准方程;
【例2】与椭圆具有相同的离心率且过点的椭圆的标准方程
【答案】1、; 2、或 ; 3、
【分析1】根据椭圆的定义及长半轴长及焦距之间的关系,可得a,b,c
【详解2】由已知条件可得,可得,,因此,所求椭圆的标准方程为;
【分析2】有椭圆的定义可知离心率和a、c之间的关系
【详解2】易知椭圆的离心率.当所求椭圆的焦点在x轴上时,可设椭圆的方程为,把点代入方程,得.又,解得,,所以所求椭圆的方程为.当所求椭圆的焦点在y轴上时,同理可设椭圆的方程为,
把点代入方程,得.又,解得,,所以所求椭圆的方程为.
【课堂练习】
1、已知椭圆的上顶点为,右顶点为,若过原点作的垂线交椭圆的右准线于点,点到轴的距离为,则此椭圆的离心率为( )
A. B. C. D.
【答案】C
【解析】由题可知,椭圆的焦点在轴上,
则,所以,
由于点在椭圆的右准线上,且到轴的距离为,
则,所以,
由题得,,则,
即,则有,即,
而,所以,
整理得:,则,即,
解得:,
即椭圆的离心率为.
2、(安徽模拟)已知椭圆的左,右焦点分别为F1,F2,若在直线上x=2a存在点P使得线段PF1的垂直平分线过点F2,则离心率范围是
【答案】
【分析】
数形结合,结合题目所给条件画出图形,懂得画垂直平分线。
发现不等式,利用椭圆离心率可得结论。
【详解】
【学习目标】
理解椭圆的定义及椭圆的标准方程.
掌握用定义法和待定系数法求椭圆的标准方程.
理解椭圆方程与离心率之间的关系,能通过属性结合进行代数的求解离心率
【重点】椭圆的定义及椭圆的标准方程
【难点】运用标准方程解决相关问题,特别是数形结合的知识内容
焦点在x轴上 焦点在y轴上
标准方程
图形
焦点坐标
对称轴 关于x轴,y轴轴对称,关于原点周彪中心对称
半长轴 长轴
半短轴 短轴
半焦距 焦距
半通径 通径
如图:,
【重点】离心率代数的转换及不等式的求解
离心率:
离心率越大,椭圆越扁;离心率越小,椭圆越圆。
【知识点】
椭圆的定义
椭圆定义的应用
椭圆的标准方程
椭圆方程与离心率
【知识点】椭圆的定义
【例1】设P是椭圆上的点.若是椭圆的两个焦点,则等于( )
A.4 B.5 C.8 D.10
【课堂练习】
1、若椭圆上一点到其焦点的距离为6,则到另一焦点的距离为( )
A.4 B.194 C.94 D.14
【知识点】椭圆定义的运用
【例1】(2019福建高二期末)如果表示焦点在轴上的椭圆,那么实数的取值范围是( )
B. C. D.
【例2】过椭圆的一个焦点,且垂直于轴的直线被此椭圆截得的弦长为
【例3】直线被椭圆截得的弦长是( )
A. B. C. D.
【例4】已知点分别是椭圆的左、右焦点,点在此椭圆上,则的周长等于( )
A.20 B.16 C.18 D.14
【课堂练习】
1、如果方程表示焦点在x轴上的椭圆,则实数a的取值范围是( )
A. B. C.或 D.或
2、已知椭圆与直线交于,两点,且,则实数的值为( )
A. B. C. D.
3、已知P是椭圆上的一点,F1,F2是椭圆的两个焦点,且∠F1PF2=60°,则△F1PF2的面积是______.
【知识点】椭圆的标准方程
【例1】焦点在轴上,长轴长为,焦距为的椭圆标准方程;
【例2】与椭圆具有相同的离心率且过点的椭圆的标准方程
【课堂练习】
1、已知椭圆的上顶点为,右顶点为,若过原点作的垂线交椭圆的右准线于点,点到轴的距离为,则此椭圆的离心率为( )
A. B. C. D.
2、(安徽模拟)已知椭圆的左,右焦点分别为F1,F2,若在直线上x=2a存在点P使得线段PF1的垂直平分线过点F2,则离心率范围是
第八讲 椭圆方程与离心率
【学习目标】
理解椭圆的定义及椭圆的标准方程.
掌握用定义法和待定系数法求椭圆的标准方程.
理解椭圆方程与离心率之间的关系,能通过属性结合进行代数的求解离心率
【重点】椭圆的定义及椭圆的标准方程
【难点】运用标准方程解决相关问题,特别是数形结合的知识内容
焦点在x轴上 焦点在y轴上
标准方程
图形
焦点坐标
对称轴 关于x轴,y轴轴对称,关于原点周彪中心对称
半长轴 长轴
半短轴 短轴
半焦距 焦距
半通径 通径
如图:,
【重点】离心率代数的转换及不等式的求解
离心率:
离心率越大,椭圆越扁;离心率越小,椭圆越圆。
【知识点】
椭圆的定义
椭圆定义的应用
椭圆的标准方程
椭圆方程与离心率
【知识点】椭圆的定义
【例1】设P是椭圆上的点.若是椭圆的两个焦点,则等于( )
A.4 B.5 C.8 D.10
【答案】D
【分析】有椭圆的定义可得,椭圆上的点到焦点的距离之和是定长。
【详解】因为椭圆的方程为,所以a2=25,由椭圆的的定义知
【课堂练习】
1、若椭圆上一点到其焦点的距离为6,则到另一焦点的距离为( )
A.4 B.194 C.94 D.14
【答案】D
【分析】由椭圆的定义可得,椭圆上的点到焦点的距离之和是定长。
【详解】依题意,且
【知识点】椭圆定义的运用
【例1】(2019福建高二期末)如果表示焦点在轴上的椭圆,那么实数的取值范围是( )
B. C. D.
【答案】A
【分析】利用椭圆的定义,化简为标准方程,根据椭圆焦点所在轴的位置判断对应的a和b的大小。
【详解】
转化为椭圆的标准方程,得,因为表示焦点在y轴上的椭圆,所以,解得.所以实数k的取值范围是(0,1)
【例2】过椭圆的一个焦点,且垂直于轴的直线被此椭圆截得的弦长为
【答案】3
【分析】过椭圆的一个焦点,且求与焦点所在轴垂直的弦叫做椭圆的通径,其长
【详解】:,,所求弦长就是椭圆通径的长度
【例3】直线被椭圆截得的弦长是( )
A. B. C. D.
【答案】A
【分析】直线被椭圆截得的弦的长度求法公式:①;②.
解题时灵活选择,使得简化过程.
【详解】联立,得.
设直线被椭圆所截线段的两个端点分别为,.
思路1:
由韦达定理,得,,则
.
思路2:
解方程,得,,则
===.
【例4】已知点分别是椭圆的左、右焦点,点在此椭圆上,则的周长等于( )
A.20 B.16 C.18 D.14
【答案】C
【分析】根据椭圆的定义得出a,b,c,画出草图即可求得周长所对应的线段长度,灵活利用a,b,c,三者之间的关系。
【详解】根据椭圆方程可知,根据椭圆的定义可知,的周长为
【课堂练习】
1、如果方程表示焦点在x轴上的椭圆,则实数a的取值范围是( )
A. B. C.或 D.或
【答案】D
【分析】利用椭圆的交点在x轴上,能得到长半轴大于短半轴,从而得到不等式,解不等式时需要注意长半轴和短半轴需同时满足大于0.
【详解】椭圆的焦点在轴上,,解得或,故选D.
2、已知椭圆与直线交于,两点,且,则实数的值为( )
A. B. C. D.
【答案】A
【分析】对于此题,弦长公式选择“”,计算相对方便
【详解】联立方程组,消,得.
>0,16>0,.
设,,根据韦达定理,有,.
,,=,.
,符合.
3、已知P是椭圆上的一点,F1,F2是椭圆的两个焦点,且∠F1PF2=60°,则△F1PF2的面积是______.
【答案】
【分析】根据椭圆的定义画出草图,根据图像可以得到三角形的图形关系示意图,灵活运用余弦定理可以求得面积。
【解析】∵|PF1|+|PF2|=4,,又∵∠F1PF2=60°,
由余弦定理可得|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos60°
12=(|PF1|+|PF2|)2-2|PF1|·|PF2|-|PF1|·|PF2|,∴,
∴.
【知识点】椭圆的标准方程
【例1】焦点在轴上,长轴长为,焦距为的椭圆标准方程;
【例2】与椭圆具有相同的离心率且过点的椭圆的标准方程
【答案】1、; 2、或 ; 3、
【分析1】根据椭圆的定义及长半轴长及焦距之间的关系,可得a,b,c
【详解2】由已知条件可得,可得,,因此,所求椭圆的标准方程为;
【分析2】有椭圆的定义可知离心率和a、c之间的关系
【详解2】易知椭圆的离心率.当所求椭圆的焦点在x轴上时,可设椭圆的方程为,把点代入方程,得.又,解得,,所以所求椭圆的方程为.当所求椭圆的焦点在y轴上时,同理可设椭圆的方程为,
把点代入方程,得.又,解得,,所以所求椭圆的方程为.
【课堂练习】
1、已知椭圆的上顶点为,右顶点为,若过原点作的垂线交椭圆的右准线于点,点到轴的距离为,则此椭圆的离心率为( )
A. B. C. D.
【答案】C
【解析】由题可知,椭圆的焦点在轴上,
则,所以,
由于点在椭圆的右准线上,且到轴的距离为,
则,所以,
由题得,,则,
即,则有,即,
而,所以,
整理得:,则,即,
解得:,
即椭圆的离心率为.
2、(安徽模拟)已知椭圆的左,右焦点分别为F1,F2,若在直线上x=2a存在点P使得线段PF1的垂直平分线过点F2,则离心率范围是
【答案】
【分析】
数形结合,结合题目所给条件画出图形,懂得画垂直平分线。
发现不等式,利用椭圆离心率可得结论。
【详解】
