18。2 勾股定理逆定理(二)勾股数[下学期]
文档属性
| 名称 | 18。2 勾股定理逆定理(二)勾股数[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 640.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-25 21:59:00 | ||
图片预览






文档简介
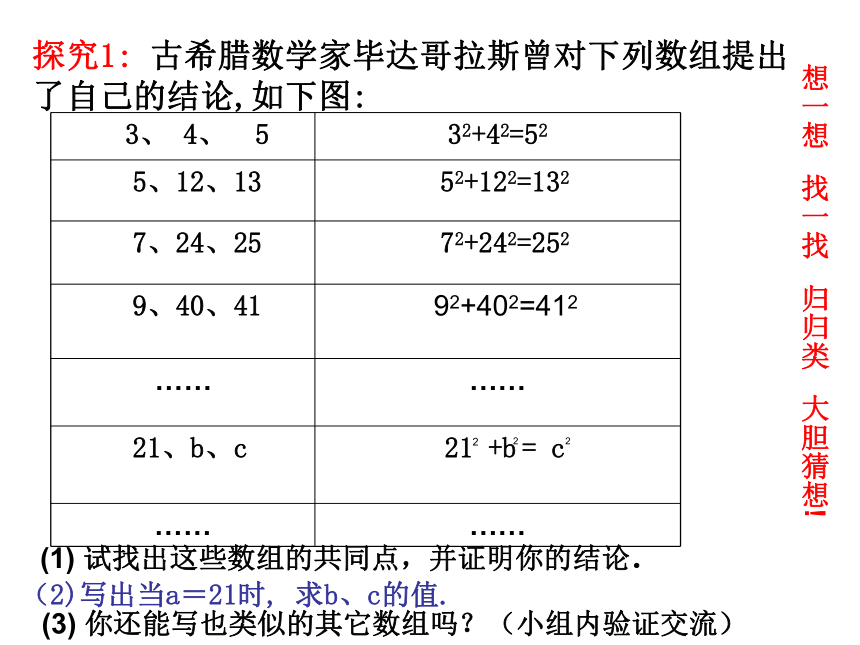
课件14张PPT。学海中学 何邦辉18.2 勾股定理的逆定理(二) 勾股数问题: 判断由线段a、b、c组成的三角形是不是直角三角形? a=8 b = 15 c =17
(2) a=13 b = 14 c =15像8、15、17这样,能够成为直角三角形三条边长的三个正整数,称为勾股数。谈谈勾股数的特征:(1)a、b、c三数都是正整数,且a 探究2:(1)请你根据上述四组勾股数的规律,写出第 五组勾股数。(2)试用数学等式描述上述勾股数组规律。(3)请证明你所发现的规律。(3、 4、 5), (8、 6、 10),(15 、 8、 17),(24、10、26)…
等等,这些数组也叫柏拉图数组。
1、下列数组中,不是勾股数的是( )
A、3k、4k、5k(k为正整数)B、5、12、13
C、7、24、25 D、8、12、13D练一练2、已知下列命题:
(1) 如果a、b、c是一组勾股数,那么 ka、kb、kc( k是正整数)仍是勾股数。(2) 如果直角三角形的两边是3、4,那么斜边必是5。(3) 如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形。(4) 2499、100、2501是一组勾股数组。其中正确的是(1),(4)验证古希腊数学家丢番图给的数组公式:
若 a=2mn,b=m2-n2,c=m2+n2 ,其中m,n 是互质的任意正整数,且m >n ,则a、b、c为勾股数.
例题精讲1、直角三角形有一条直角边长为11,另外两边的长也是正整数,求此三角形的周长.? 思考? 2、一个直角三角形的边长都是正整数,它的面积和周长的值相等,这样的直角三角形存在吗?若存在,确定它三边的长。数 海 拾 贝 从代数的角度看勾股数,就是考察方程 + = 的正整数解,古代中国人发现了”勾三股四弦五”,古希腊人找到了这个方程的全部整数解.
17世纪,法国数学家费马提出猜想:当n≥3时,方程
+ = 无正整数解,围绕着这个看似简单的费马大定理,一批杰出的数学家,如欧拉,柯西,伽罗华,还有维尔斯,他们前赴后继用了整整358年才最后完成这项证明.
费马大定理被人比作数论中的“喜马拉雅山的顶峰”
≥2zxyn22xyznn忠诚感谢您的参与再见
(2) a=13 b = 14 c =15像8、15、17这样,能够成为直角三角形三条边长的三个正整数,称为勾股数。谈谈勾股数的特征:(1)a、b、c三数都是正整数,且a
等等,这些数组也叫柏拉图数组。
1、下列数组中,不是勾股数的是( )
A、3k、4k、5k(k为正整数)B、5、12、13
C、7、24、25 D、8、12、13D练一练2、已知下列命题:
(1) 如果a、b、c是一组勾股数,那么 ka、kb、kc( k是正整数)仍是勾股数。(2) 如果直角三角形的两边是3、4,那么斜边必是5。(3) 如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形。(4) 2499、100、2501是一组勾股数组。其中正确的是(1),(4)验证古希腊数学家丢番图给的数组公式:
若 a=2mn,b=m2-n2,c=m2+n2 ,其中m,n 是互质的任意正整数,且m >n ,则a、b、c为勾股数.
例题精讲1、直角三角形有一条直角边长为11,另外两边的长也是正整数,求此三角形的周长.? 思考? 2、一个直角三角形的边长都是正整数,它的面积和周长的值相等,这样的直角三角形存在吗?若存在,确定它三边的长。数 海 拾 贝 从代数的角度看勾股数,就是考察方程 + = 的正整数解,古代中国人发现了”勾三股四弦五”,古希腊人找到了这个方程的全部整数解.
17世纪,法国数学家费马提出猜想:当n≥3时,方程
+ = 无正整数解,围绕着这个看似简单的费马大定理,一批杰出的数学家,如欧拉,柯西,伽罗华,还有维尔斯,他们前赴后继用了整整358年才最后完成这项证明.
费马大定理被人比作数论中的“喜马拉雅山的顶峰”
≥2zxyn22xyznn忠诚感谢您的参与再见
